南外省选集训
NOIP后南外省选集训
NOI2024省选训练赛5
A. 两棵树
原题是BZOJ crash和陶陶的游戏

$n\le 10^5$
考虑加入一个 $A$ 树的叶子对答案的贡献是 $B$ 中的祖孙链上的子串数, 更好的是 $A$ 这个叶子作为 $B$ 字典树上的后缀的个数, 加入 $B$ 的叶子相当于对 $A$ 的字典树的一条从根的链求和.
具体的考虑如何解决 $A$, 相当于求字典树的子串出现次数, 相当于阿狸的打字机带修. 或者考虑直接求出 $B$ 字典树上所有字符串的字典序排序, 这样包含一个串的一定是一个后缀, 就是区间问题了.
考虑如何解决 $B$, 需要先匹配一下 $B$ 这个叶子往上跳多远还在 $A$ 里, 然后随便求和.
于是可以维护出 $B$ 中每个点 $u$ 向上跳 $2^i$ 步的hash值, 这个可以同时用于求字典序排序和 $B$ 这个叶子往上跳多远的问题.
B. 头文字 O
你在无限的数轴上从 $0$ 开始随机游走 $n$ 步, 每次位置 $+- 1$, 由 $m$ 个给定的区间, 若你的路径中存在一段以 $s_i$ 开头, $t_i$ 结尾则会获得 $v_i$ 价值, 求价值期望.
$n\le 2\times 10^5, m\le 5\times 10^5$
一眼反射容斥.
然后做这个题的时候以为它数轴有界, 这时候两边都要反射情况有点多.
首先期望线性性, 对每个 $s, t$ 算, 如果 $s<0$ 你可以把 $s, t$ 都取负, 如果 $t<s$ 可以把 $t$ 对称到另一边,这样走到 $s$ 之后的路径对称构成双射.
于是很棒的, $0<s<t$, 这意味着我们只用管经过 $t$ 这个条件, 这就先求不经过 $t$ 的, 枚举终点后是经典反射容斥, 对所有终点累加是上指标均为 $n$ 的组合数之和, 前缀和即可.
如果没有观察到双射怎么处理, 那就枚举一个步数 $l$, 先走到 $s$ 的方案数和从 $s$ 出发走 $l$ 步不经过 $t$ 的方案数卷起来, 硬推组合式应该也能做.
C. 慈善

$n, m\le 2\times 10^5, C, a, b, c, d\le 10^{18}$
考虑一些dp, 比如 $f_{i, j, k}$ 表示 $i$ 时刻两人收益分别为 $j, k$, 然后你会想到相当于维护点集 $(j, k)$, 在处理两人一起抽卡的时候应该发现维护 $k-j, k$ 比 $j, k$ 好, 然后三种情况(小H抽, 小X抽, 一起抽)就是点集和向量做闵和, 然后你又想到点集其实只有 $y$ 最大的有用也就成了函数, 于是开始维护函数.
那么设这个时间段长为 $t$, 小H抽卡是和 $(t, t)$ 做闵和, 小X抽卡是和 $(-t, 0)$ 做闵和, 同时抽卡是一部分点和 $(t, 0)$, 一部分点和 $(2t, 0)$ 做闵和.
考虑如何维护这个分段函数直接维护显然做不了, 发现这个函数可以分成若干段, 其中每一段中的点是经由相同的转移过来的, 值相同, 而段的端点就可以代表这个走的过程, 设左右端点分别是 $(l, y_1), (r, y_2)$, 这个段内的点 $(x, y)$ 可能是由左边放弃若干X抽卡得到 $(x, y_1)$, 也可能是右边放弃若干H抽卡得到 $(x, y_2-r+x)$, 也就是一个段内的点是它俩取 $max$ 得到, 于是我们只维护关键点的 $y$ 值即可, 则 $-t$ 和 $t, t$ 可以直接平移和全局加, 而第三种操作会让 $[-C, C]$ 内的点路径和两边的不同, 于是要新插入 $C, -C$ 作为关键点, 然后给它们之内的点整体加.
可以写平衡树, 也可以先模拟一遍操作 $1, 2$ 的平移得到关键点实际上应该都插入到哪用线段树.
D. 卡牌高手
背包, 第 $i$ 种物品有 $c_i$ 种体积为 $w_i$, $m$ 次操作单点修改 $c$ 或者询问编号在 $[l, r]$ 中的物品的多重集体积和不超过 $k$ 的有多少种.
$n, m, w_i\le 5000$, 任意时刻 $\sum_i c_iw_i\le 5000$
显然让你卷区间的 $\dfrac{1-x^{w_i(c_i+1)}}{1-x^{w_i}}$
赛时没注意到任意时刻那部分, 对着加起来的ln不会优化exp.
于是可以直接线段树维护点值, 然后每次询问都乘起来做一次idft, 复杂度是 $8192(n+m\log n+m\log 8192)$
此外, 求点值不如直接把单位根带到封闭形式里.
极度卡常, 不如暴力
NOI2024省选训练赛6
A, C, D是之前做过的模拟赛大原题
B 最大战略储备
原题是 P4809 [CCC2018] 最大战略储备
有 $N$ 个星球, 编号为 $1\ldots N$. 每个星球有 $M$ 座城市, 编号为 $1\ldots M$. 我们将 $e$ 星球上的城市 $f$ 记作 $(e, f)$.
有 $N\times P$ 条双向航线, 对于每个星球 $e(1\le e\le N)$, 有 $P$ 条航线, 编号为 $1$ 到 $P$. 第 $i$ 条航线连接城市 $(e, , a_i)$ 和 $(e, , b_i)$, 且每天需要花费 $c_i$ 的代价维护.
有 $M\times Q$ 个双向港口. 对于所有编号为 $f(1\le f\le M)$ 的城市, 有 $Q$ 个港口, 编号为 $1$ 到 $Q$. 第 $j$ 个港口可以连接城市 $(x_j, , f)$ 和 $(y_j, , f)$, 且每天需要花费 $z_j$ 的代价维护.
现在需要拆除一些港口和(或)取消一些航线, 使得城市之间仍能保持联通, 且节省的代价之和最大.
对于全部的数据, $1\le N, , M, , P, , Q\le10^5$.
考虑把 $(e, f)$ 画成一个网格, 则一开始每行连的边相同, 每列连的边相同, 那么可以先分别求出最小生成树.
现在把两个的最小生成树的边合到一起排序从小到大加边, 一次加一排有环的跳过显然就是对的, 一个很显然的结论是若与当前加边方向不同的边加了 $x$ 条, 当前方向本来要加 $n$ 条, 则现在只要加 $n-x$ 条, 就是因为与当前方向不同的每加一次相当于减少一列点, 于是就做完了.
ICPC模拟赛2
看起来是 2023牛客暑期多校训练营9
E. Puzzle: Square Jam
$n \times m$ 网格, 划分成正方形使得没有任何一个点和四个正方形相邻.
简单想想发现每次都取短边长度贴着一边放即可递归下去辗转相减.
坐标输出反了wa了一发/fn
D. Non-Puzzle: Error Permutation
给定长度为 $n$ 的排列, 计算有多少个子区间满足子区间第 $k$ 小的数不在
子区间第 $k$ 位. $n \le 5000$.
考虑枚举左端点和区间内一个点, 要使得这个点不在第 $k$ 位, 考虑其限制右端点不能在一个区间, 这个区间的限制也就是区间内有几个比它小的数, 直接预处理出小于 $i$ 的数的位置 $p_{i, \ldots}$ 和 $i$ 在小于 $j$ 的数中是从前到后第几个 $id_{j, i}$, $n^2$
多测清空没清干净wa了两发/fn
I. Non-Puzzle: Segment Pair
给定 $n$ 对区间 $l_i, r_i, l_i’, r_i’$, 每对中选择一个使得所有选择的至少包含一个公共点, 问方案数.
$n\le 5\times 10^5$
首先最后的交肯定是个区间, 那么考虑直接计算包含某一点有多少种方法, 这个只要算有多少对区间的交/并包含当前点, 但这样会算重, 考虑钦定当前点是最后交的左端点, 这样只要减掉同时包含 $i, i-1$ 的就做完了.
下标偏了一位wa了三发.
G. Non-Puzzle: Game
Alice 和 Bob 博弈, Alice先手. 黑板上原有 $n$ 个数 $a_i$, 每次当前行动方可以选择一对 $(i, j)$, 并在黑板上写上 $a_i \mathrm{xor} aj$. 先写下 $k$ 的人胜利. 问博弈结果, 或者平局(无穷局下两人谁也不会写出 $k$).
$n\le 10^6, a_i\le 2^{30}$
考虑拿到 $k$ 前的那一步显然谁走那一步谁就输, 所以大家会不断开摆进行无效操作(重复之前的某次操作即可), 那么要想不平只有大家都没有之前的步子可重复的清空, 即只要判定Alice能不能第一步直接获胜和有没有Alice不管怎么走Bob第二步直接获胜, 第一个判定显然, 第二个判定就等价于 $a_i\mathrm{xor} a_j=a_p\mathrm{k}\Rightarrow (a_i\mathrm{xor} k) \mathrm{xor}(a_j\mathrm{xor} k)=a_p\mathrm{xor} k$, 于是就是判定 ${a_i}$ 在异或 $k$ 下封闭, 只要求线性基然后判断不同元素个数是否是能表示的所有数.
[trick] 利用异或性质写式子.
F. Non-Puzzle: The Lost Array
对于序列 $a_n$, 令 $num_i$ 表示数字 $i$ 出现的次数, 统计满足条件的序列个数:
- $1 \leq a_i \leq m$
- 给定一些 $x_i, y_i$, 满足 $a_{x_i} \neq y_i$
- 给定一些 $x_i, y_i$, 满足 $num_{x_i} \neq y_i$.
- 将 $num$ 排序后, 得到一给定序列 $B$.
$n\le 16, m\le 30$
正经人dp肯定是扫值, $f_{i, S, T}$ 表示当前扫了前 $i$ 个数, 能填的位置集合还有 $S$, 剩下还没填的值的出现次数的多重集是 $T$, 注意到 $T$ 很小, 爆搜完了最大 $72$, 复杂度是 $3^nnm72$(转移时要枚举子集).
考虑优化掉集合 $S$ 这一维, 容斥它:
实际上要做的是从 $m$ 个数选出 $n$ 个数组成值集合, 然后到位置集合 ${1\ldots n}$ 做双射, 那么现在改成, 设 $f(S)$ 表示值集合和位置集合 $S$ 做双射的方案数(所以 $S$ 为全集时就是答案), $g(S)$ 表示值集合和位置集合任意映射的方案数(一个位置可以填多个值), 那么有 $g(S)=\sum_{T\subseteq S}f(T)$, 于是 $f(S)=\sum_{T\subseteq S}g(T)(-1)^{\vert S\vert-\vert T\vert}$
[trick] 填排列都可以转化成值和位置做映射容斥掉每个位置只能填一次的限制. 同样例题还有ZJOI小星星.
于是复杂度 $2^nnm72$. 很厉害啊这个trick.
NOI2024省选模拟赛7
A. 小 W 的滑雪比赛
小W要参加滑雪比赛啦! 滑雪场有一条主干道, 从海拔为 $H$ 的山顶到海拔为 $0$ 的山脚. 主干道两边有 $n$ 个检查站, 第 $i$ 个距离主干道 $X_i$(为正在右边, 为负在左边), 海拔为 $Y_i$, 如果通过会获得分数 $S_i$. 多次经过同一个检查站分数只会计一次, 没有两个检查站位置相同.
小W想要通过其中一些检查站, 最大化自己的得分. 为了防止在小G面前出丑, 小W基于实地考察评估了每个检查站的容易程度 $E_i$(越大越容易), 能够从 $i$ 滑到 $j$ 当且仅当 $\max(\vert X_i - X_j\vert , Y_i - Y_j) \leq E_i$ 且 $Y_i \geq Y_j$, 并且从山顶可以到达任何检查站, 从任何检查站可以到达山脚.
请你帮助小W计算出得分之和的最大值.
$n, H\le 10^5$
不是, 为啥kdt的根号过不了1s $2\times 10^5$ /fn
总之这是简单dp题, 按照 $y$ 排序, 设到第 $i$ 个点的代价为 $f_i$, 可以化成单点改矩形max.
考虑把修改查询均衡一下, 那么可以变成每次对纵向线段取max, 查询一条横向线段的最大值, 这样在 $y$ 从小到大的过程中, 纵向建线段树, 每个点维护单调栈, 标记永久化, 复杂度2log.
好强好强, kdt单点加矩形max, 查询时大于当前值就不查了, 加剪纸跑的飞快.
B. 数树
给定连通图 $G(V, E)$, 保证不存在从节点 $1$ 开始经过 $8$ 个点的简单路径, 求生成树个数, 模 $2^30$
$n\le 5\times 10^4, m\le 10^5$
你就不能模的质数吗(
考虑dp, 建出以 $1$ 为根的dfs树显然深度不超过 $8$, 而对于一个点其连边方案只和到根的路径上的点的连通性有关, 状压记录这个即可转移, 状态数是 $m\cdot Bell(7)$, 转移的时候需要合并子树内的连通性可能不对?
考虑按照dfs序dp, 你仍然只需要记录刚才我们说的内容, 但变成了逐个加点, 转移就 $O(1)$ 了.
C. LJJ的农场
给定 $a_n, b_n$, 并 $q$ 次单点改大 $a, b$, 每次询问后求 $\min_{i, j} j\cdot a_i+i\cdot b_j$
$n, q\le 10^5$
乍一看是二元变量, 但实际上固定住一个之后仍然是正常斜率优化, 常见的斜率优化是 $y=kx+b$ 最小化 $b$, 这个相当于 $ax+by=c$ 最小化 $c$, 那么直接平衡树维护凸壳就做完了, 是下凸壳改大, 所以要倒着做改小变成向凸壳加点而不是删点.
更简答的直接李超树, 然后也是需要倒着走变成每次加线段而不能删.
D. 黑白点
平面上给定 $n$ 个黑点, 进行 $m$ 轮操作, 每轮加入一个白点.
你需要在每次加点操作后求出: 最少删去多少黑点和白点使得不存在黑点 $(x, y)$ 和白点 $(x’, y’)$ 满足 $x\le x’, y\le y’$.
$n\le 10^5$

NOI2024省选训练赛8
A. 气球
有 $n$ 个气球, 一开始都是空的. 然后按照从 $1$ 到 $n$ 的顺序依次充气, 其中第 $i$ 个气球在充气过程中始终与地面 $x_i$ 位置接触, 保证 $x_i$ 单调增. 当气球碰到前面的某个气球, 或者达到半径最大限制 $r_i$ 时, 就会停止充气. 请求出每个气球最终半径是多少.
$n\le 5\times 10^5$
列出式子发现若气球 $1, 2$ 接触, 则 $2\sqrt{r_1}\sqrt{r_2}=x_1-x_2$, 斜率优化即可.
B. mwhak
小 A 和小 B 是两条蛇, 他们正在一棵特殊的树上做游戏.
这棵树的结构如下: 首先有一条长度为 $n$ 的链, 称为”主链”. 主链由 $1$ 至 $n$ 这 $n$ 个节点构成. 在主链上, 编号相邻的点有边相连, 否则则没有.
主链上的每一个点都挂着一条链, 称为”副链”. 主链上的第 $i$ 个点挂的副链长度(链上的点数)为 $x_i$.
小 A 和小 B 初始时都在主链上, 具体而言, 小 A 的蛇尾在点 $a$, 蛇头在点 $b$, 小 B的蛇头在点 $c$, 蛇尾在点 $d$. 满足 $1\leq a<b<c<d\leq n$.
他们的游戏规则如下:
小 A 和小 B 轮流移动, 小 A 先手.
- 每条蛇移动时, 他会尝试整体向某一方向移动一个节点, 但不能向原来蛇尾方向移动, 也就是蛇不能倒退. 需满足移动后蛇头不得与另外一条蛇的任意部分重合.
- 当一条蛇无法移动时, 游戏结束, 对手获胜.
现在 $mwh$ 有 $q$ 次询问, 每次询问给定 $a$, $b$, $c$, $d$, $mwh$ 想知道当两条蛇都采取最优策略时, 哪一条蛇会获胜.
$n, q\le 10^6$
考虑两条蛇什么时候会拐入一条副链 $x_k$, 一定是进去之后能赢, 也就是要满足不存在在这条链以后不存在另一条副链使得对方拐进去会赢, 对方不能跟着自己进入自己的副链. 然后求出两方会拐入的副链, 更早拐入的胜, 下面对A分析.
第二个限制是 $k-a>c-k\rightarrow k>\dfrac{a+c}{2}$, 第一个限制是 $k-b+x_k\ge c+ \max_{j\in [k+1, c-(k-b)]} x_j-j$ 可以化简成 $x_k+k\ge b+c+\max_{j\in [k+1, b+c-k]} x_j-j$, 发现 $b+c$ 一起出现, 并且固定 $k$ 这个式子关于 $b+c$ 单调, 于是每个 $k$ 能拐的情况下 $b+c$ 是一个前缀.
那就好做了, 先二分出每个 $k$ 对应的 $lim_k$ 表示 $b+c\le lim_k$, 询问时再去二分第一个 $lim_k\ge b+c$ 的位置即可.
C. 数据结构
给定一个有 $n$ 个 $01$ 字符串的字符串集合, 每个字符串有一个代价. 再给定 $01$ 字符串 $T$. 你有一个串 $S$, 初始为空串, 每次你可以从字符串集合内选一个字符串, 将其任意长度的前缀或后缀加入到 $S$ 的末尾, 代价为该字符串的代价. 字符串集合内的字符串可以重复使用. 最小化代价总和使得操作完成后 $S = T$, 或说明不存在这样的方案.
$n, m, L\le 2\times 10^5, c_i\le 10^9$
dp设 $f_i$ 表示 $i$ 为结尾的串表示出来的最小代价, 看到总长想根号分治, 那么长度小于根号的可以直接每次枚举这个长度的, 贡献可以用trieac机随便什么算. 大于根号的可以直接每个串单独算, 那么需要知道每个位置向前向后能在这个串上匹配多远, kmp就能做, 做完了之后会转化成区间取min单点查和单点修改区间min, 用分块平衡以下即可.
总复杂度单根号.
D. 礼物
有一棵 $n$ 点树, 给定删掉点 $a$ 及其相连的边并打乱点的编号后得到的森林 $A$, 以及删掉 $b$ 并打乱点的编号后得到的森林 $B$, 给定 $A, B$, 求一个可能的原树.
$n\le 2000$
考虑枚举 $A$ 上的点 $b$, $a$ 和 $B$ 中的点 $a$, 如何判断是否合法, 最直接的想法是都删掉判断剩下的集合对不对, 但这个是假的, 如图不能区分 $a’$ 和 $a’’$:
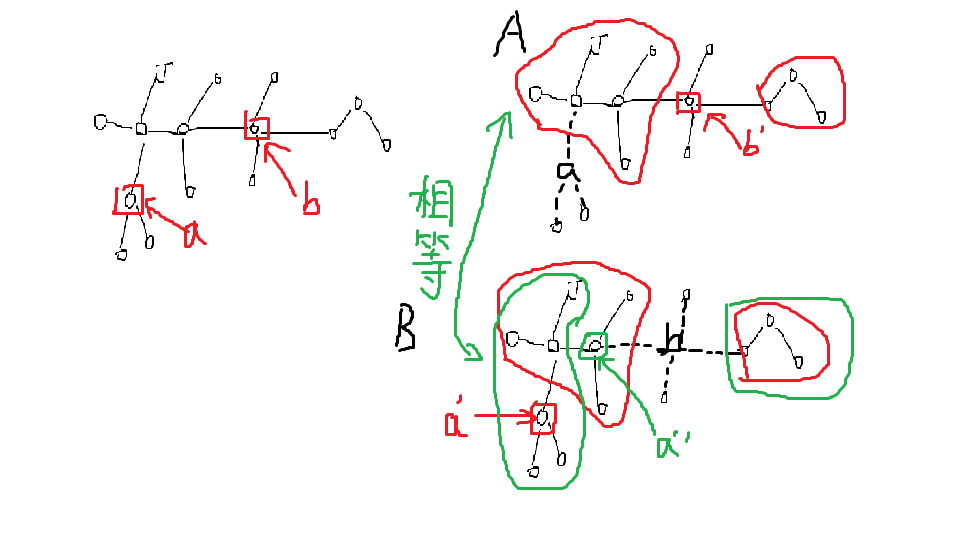
假的原因是没有判断连通块的位置关系, 对于 $a’$ 那个最大的连通块是在 $a, b$ 中间的, 而 $a’’$ 中这个大连通块与 $a$ 相连而不与 $b$ 相邻, 加上这个条件:
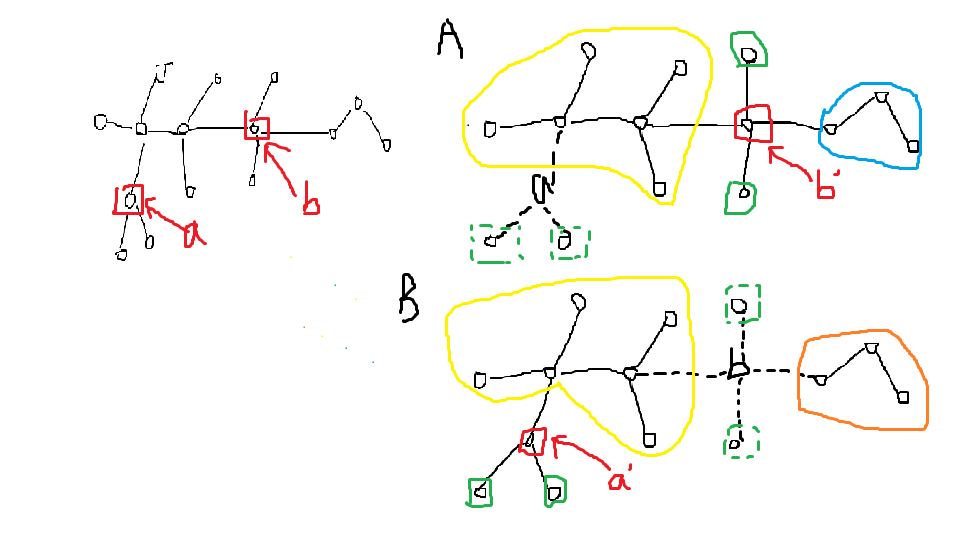
如图, 枚举之后, 把连通块分成与 $a$ 相连, $a, b$ 之间, 与 $b$ 相连的和单点四部分, 那么对于图 $A$, 与 $a$ 相连的部分就是删掉 $b$ 前和 $b$ 不在同一连通块的点, $a, b$ 之间的就是与 $b$ 相连的连通块中枚举一个, 剩下的是与 $b$ 相连的, 单点直接判断了, 于是会获得 $n^2$ 个连通块集合对 $(S_1, S_2, S_3, S_4)$ 表示四部分, 只要都树哈希掉, 再和 $B$ 中枚举 $a$ 获得的集合对找相等的即可.
NOI2024省选训练赛9
A. 圆弧
圆上 $3n$ 个点, 点有颜色, $n$ 种颜色每种色出现恰好 $3$ 次, 你要给每个颜色 $c$ 的两个点画一条弧, 满足不经过第三个为颜色为 $c$ 的点, 要求 $n$ 条弧互不相交(也不能包含). 求方案数模 $998244353$
$n\le 2\times 10^5$
枚举一个颜色的弧, 就可以把环转成序列问题.
然后暴力是 $f_{i, j}$ 表示前 $i$ 个点画 $j$ 条弧的方案数, 那么因为最后 $j=n-1$, 发现大部分 $j$ 是到不了的, 实际上是对最大画线方案计数, 所以每个 $i$ 对应了唯一的 $j$, 复杂度 $O(n)$
B. 整除
给定 $m, a_n, c_n$, 求有多少正整数 $x$ 满足 $(\sum_{i=0}^{m-1} x_i)\vert (\sum_{i=0}^{a_i} c_ix^{a_i})$($\vert$ 指整除), $n\le 10^5$
容易想到左边变成 $\dfrac{x^m-1}{x-1}$, 然后乘到右边 $(x-1)$, 再对 $x^m-1$ 多项式取模得到新的多项式, 设为 $\sum_{i=0}^{m-1} b_ix^i$
容易发现若 $x>maxb+1$, 则 $x^{m-1}$ 和 $x^m$ 的差距就不能靠系数了, 也就是 $x\le maxb+1$, 只有 $O(n)$ 个, 问题在于如何判定.
这个判定很巧妙, 考虑若 $b_i>x$, 则 $b_i\coloneqq b_i-x, b_{i+1\bmod m}\coloneqq b_{i+1\bmod m}+1$ 原式不变, 处理完之后所有系数都小于 $x$, 则 $x^m-1$ 能整除它当且仅当
- 都是 $0$
- 都是 $x-1$
- 都是 $1-x$
而最关键的是, 因为每一步会把 $a_i$ 缩小 $x-1$, 所以枚举所有的 $x$ 之后步数是 $n\ln n$ 的, 于是拿map维护就俩log过了.
C. 词典
哇原题[2022SDFZ省选模拟赛6] 词典, 在杂题选做中.
重要的是先考虑
现在看来更套路一点了, 见到这个肯定想字典树, 然后就是dp->猜凸性->闵和min+卷积套路.
此外不太常见的就是这个dp式子列出来相当于”半在线min+卷积”, 但都是能做的.
D. 蒲公英
给一棵直径小于 $4$ 条边的树, 要求给点重新编号 $1\ldots n$ 使得每条边两边的的差的绝对值构成排列
$n\le 10^5$
智慧题啊.
我们可以轻易地发现, 如果取直径的中点为根, 那么树的高度不会超过2. 因此, 我们可以用 $a_1, a_2, \ldots, a_k$ 来描述树的形态, 其中根有 $k$ 个子节点, 第 $i$ 个节点有 $a_i$ 个儿子.
首先, 我们考虑所有的 $a_i$ 都不为零, 且 $k = 2m + 1$ 为奇数的情况. 我们让根节点的重标号为 $1$. 然后, 我们按照奇偶性将 $a_i$ 分离, 将奇数置于前面, 偶数置于后面. 接下来, 我们需要交替地填入”还没有填入的最小标号”和”还没有填入的最大编号”, 我们分别用 $L$ 和 $R$ 来表示. 首先, 我们给根节点的所有儿子交替填入 $L$ 和 $R$ (按照奇偶性分离后的结果). 然后, 我们依次考虑根节点的各个儿子, 对于前面的奇数部分, 我们依次给它的子节点交替填入 $L$ 和 $R$ ; 对于后面的偶数部分, 我们先留下它的一个子节点, 对于剩下的奇数个子节点, 我们交替填入 $L$ 和 $R$ . 最后, 我们倒序考虑根节点的儿子, 如果它有偶数个儿子, 我们就把原来留下的那个按照目前交替到的情况填数. 这个填法的正确性是比较容易验证的.
如果 $k = 2m$ 为偶数, 我们随便取根节点的一个儿子, 让这个点重标号为 $n$ . 假设它有 $p$ 个儿子, 那么我们给它的儿子标号 $1, 2, \ldots, p$ , 根节点标号 $p + 1$ . 这时, 我们会发现删掉这个子树后, 剩下的部分就相当于一个 $n - p - 1$ 的情况. 只有根节点受到了限制, 但这个限制和刚才的填法是吻合的, 所以我们可以直接填入.
最后, 如果有的 $a_i$ 为零, 我们可以根据非零的 $a_i$ 的数目的奇偶性来确定两种情况. 对于第二种情况, 我们先完成删掉子树的部分. 然后, 我们把这些没有子节点的节点都填入 $R$ (“还没有填入的最大编号”)即可.
时间复杂度为 $O(n)$ .
NOI2024省选训练赛10
A. 炮塔
$1\times n$ 的网格, 每个位置是空地
., 炮塔#和干扰器*, 你从第一个格子出发可以往左往右走, 你有一个背包, 你可以把地上的干扰器放入背包或者把背包里的干扰器放到地上, 你可以走过一个炮台当且仅当炮台相邻格子存在干扰器, 问任意长时间后背包里最多有多少干扰器.$n\le 3\times 10^6$
分类讨论题, 主要就是很难考虑全情况, 以及清晰的分类.
发现可以把曾经走过的部分的干扰器分成两类, 需要一个干扰器可以拿到并走回当前位置的和需要两个干扰器可以拿到并走回来的, 假设你在字符串中的x上, *#x需要一个, 而可以发现手拿两个干扰器可以拿到没被挡住的所有干扰器, 被挡住指##后面不是*的情况.
所以维护两类干扰器的数量和现在手里的数量, 从左往右扫一遍字符串即可.
B. 小U 与解密游戏
给定 $\texttt{01}$ 串 $s$, 每次同时交换所有的位置 $i$ 满足 $s_i=0, s_{i+1}=1$, 问 $k$ 次后字符串的样子.
$n, k\le 5\times 10^6$
可以看成所有的 $1$ 在往前走, 容易发现一个 $1$ 和前面的 $1$ 相邻时, 后面的 $1$ 会原地停一轮然后复制前面的 $1$ 的移动, 一个 $1$ 的移动可以看成一个斜率为 $0$ 和 $1$ 的线段交替的折线, 写了个维护折线的无旋treapTLE了, 然后把一个合并分裂查函数值的东西改成静态的BST上查询就过了.
然后这个东西其实deque能维护, 傻了吧.
C. 欢乐豆
有一个 $n$ 点有向完全图, $u\to v$ 的边权为 $a_u$, $m$ 次修改一条边的边权, 求出所有修改完成后图上所有点对的最短路之和.
$n\le 10^5, m\le 3000$
容易想到把这些新边拿出来成一个图, 那么要求的贡献有两类: 点对两个点都在新图上和起点在新图上. 然后注意如果你走通过非新图上边走到一个没被修改涉及的点那么一定一步到位.
对于起点在新图上终点不在新图上, 或者起点终点不在同一连通块, 一定是沿着新图走到某个位置, 然后走图外边到达终点, 直接对每个点跑dij求最短路即可.
对于两个点都在新图上的则复杂一些, 因为最优解可能走两个点都在新图上但边不在新图上的路, 如果暴力添加这些边就会 $n^3$, 考虑数据结构优化dij, 虽然不好直接维护一个没有规律的集合, 但是一个全集减去 $k$ 个点可以拆成 $k+1$ 段, 所以拿线段树实现对这些边操作, 就是区间取min, 此外要支持单点修改($m$ 条边中的边)和查最小值.
D. Musician
ZR原题 “22冲刺day18-D-Melody”, 然是ZR搬的nfls
随机化专题
放到随机化那篇文章里吧
NOI2024省选训练赛11
A. 小明去旅游2
$n$ 个三维点, $m$ 次每次给一个长方体打一个标记, 求不同的标记集合把点分成了多少种.
$n, m\le 5\times 10^4$
哈希秒了, 然后上KDT/三维偏序维护即可.
写了KDT差分(单点修改区间查询)被卡常, 点数大, 换成单点查询区间修改懒标记被卡常, 换成标记永久化过了.
B. 问题出现我再告诉大家
给一棵 $1$ 为根的 $n$ 个点的树和 ${c_n}, {d_n}$, 表示可以以 $c_u$ 代价覆盖 $u$ 子树中与 $u$ 距离不超过 $d_u$ 的点, 求每个点都被至少一个点覆盖的代价最小值.
$n\le 10^6$
暴力dp就是 $f_{u, i}$ 表示 $u$ 的子树其中最上面 $i$ 层已经被覆盖了的情况下完全覆盖的代价最小值, 然后转移是 $f_{u, i}=\min (\sum_v f_{v, i-1}, \sum_v f_v{d_u-1}+c_u)$, 所以线段树合并维护整体dp, 相当于先累加, 再平移, 再对一个值取min.
其实状态用深度就可以避免那个平移了, 然后这个是有区间修改的线段树合并, 要保证复杂度是对的需要判断, 当合并的两个点中有一个点是空点(没有孩子只有标记)的时候就直接合并退出, 于是还要再写区间加.
这样复杂度是时间 $n\log n$, 空间 $n\log n$, 已经能过了, 然后线段树每次先进重儿子+垃圾回收就可以优化成线性空间.
C. 路
给定 $n\times m$ 的网格, 有些位置有障碍物, 求有多少方式选择一个没有障碍物的点的集合使得每一条 $(0, 0)$ 走到 $(n-1, m-1)$ 且不经过障碍物的路径都经过恰好一个集合中的点.
$n, m\le 30$
输出 $n+m-1$ 获得没有障碍物的40分.
先建出原平面图, 有障碍的位置不连, 再转对偶图, 但是这里要求一条路上恰好经过一个被选中的点, 所以仍然以区域为新点, 新点是穿过原点从右上到左下的边, 那么路径条数就是答案. 然后要乘上那些到不了起点和终点的位置的乱选方案.
D. 一般难度的推式子题
求 $n$ 个点的树的高度期望.
问题是怎么表示树的高度, 考虑去掉根节点的平面树和合法括号序列是双射, 而树高就是最深的嵌套层数, 也就是对括号序列做前缀和之后的最大值.
那么考虑高度不高于 $h$ 的, 也就是数每一步可以走 $(1, -1)$ 或 $(1, 1)$, 从 $(0, 0)$ 走到 $(0, 2n-2)$, 不能碰到 $y=-1$ 和 $y=h$ 的方案数.
转化成了反射容斥典题, 考虑如果碰到上面的线记录一个 $\texttt A$, 碰到下面的线记录 $\texttt B$, 把连续的 $\texttt A$ 和 $\texttt B$ 缩成一个, 就要用系数容斥出 $\texttt {AB}$ 交替串为空, 可行的方式是对所有 $\texttt{AB}$ 串做, 系数为 $(-1)^{len}$, 然后注意到对于 $\texttt{ABABABAB}$ 这样的串, 每反射两次终点向上平移 $2h+2$, 则只要 $O(\dfrac{n}{h})$ 次方案数就是 $0$ 了, 所以求一个的复杂度是 $O(\dfrac{n}{h})$, 对所有的求复杂度就是 $n\ln n$ 了.
两条线反射容斥是EI生成函数败北里介绍的典型啊
NOI2024省选训练赛12
A. 聚会
原题 P7201 [COCI2019-2020#1] Džumbus
Marin 是一个心地善良的人, 因此他将为他的 $N$ 个朋友组织 $Q$ 次宴会. 宴会上唯一的饮料被称为 džumbus.
每位朋友对这种饮料的需求量是已知的. 在这些朋友中, 有 $M$ 组朋友. 每一组中的两位在同时满足他们各自的需求量后, 将开始互相核对自己对往届 COCI 题目的答案.
当朋友 $A$ 把自己的答案分享给朋友 $B$ 时, 朋友 $B$ 可以决定是否要以相同的方式进行分享. 然而, 这 $M$ 组朋友不可能将 $A$ 分享给别人的答案重新分享给 $A$. (无环)
对于 $100%$ 的数据, $0 \le M \lt N \le 1000, 1 \le Q \le 2 \times 10^5, 1 \le D_i \le 10^9, 1 \le S_i \le 10^9$.
一眼dp, 因为答案数量小而 $s, d$ 大维度互换, 设 $f_{u, i, 0/1/2}$ 表示 $u$ 子树内有 $i$ 个人传递答案, $u$ 自己没有满足需求量/满足需求量但没有与子节点传递/满足需求量且已传递 的情况下最小需要多少饮料即可, 最后二分
复杂度 $n^2$
B. 全国高中 IO 联赛二试
给定一棵树, 对于一个集合 $S$, 设其权值为拿出 $S$ 集合中的点并两两连边, 权值为两点在原树上的距离形成的完全图的最小生成树的边权和. 给定每个点在 $S$ 中的概率求 $S$ 的权值期望.
$n\le 1000$
一开始没有懂为什么不是最小斯坦纳树问号了好久.
考虑期望的线性性, 枚举原树上两个点 $u, v$ 考虑 $(u, v)$ 成为新的最小生成树上边的概率, 显然要求 $u\in S, v\in S, \forall w\in Chain(u, v), w\notin S$, 但这样还不够, 考虑若一个 $S$ 中点 $w$ 在这条链上某个点的子树中, 那么除了连 $u\to v, w\to u/v$, 还可以 $u\to w, v\to w$, 而选第一种的条件就是 $w$ 到这条链的距离大于 $w$ 到 $u$ 和 $v$ 的距离. 发现一个很大的问题是可能会数重最小生成树, 也就是同一个集合的两种最小生成树数两遍, 于是在原有边权上附加一维使得边权和大小相同的最小生成树被钦定了大小顺序即可.
于是只要对每个 $u, v$ 算 $u, v$ 之间的链及其子树中所有到 $u, v$ 的距离大于到 $u, v$ 链的距离的点不选的概率, 是这些点的不选的概率乘起来, 一次对一个 $u$ 算所有的 $v$ 即可 $n^2\log n$.
赛后题解是这样的, 感觉更智慧一点:
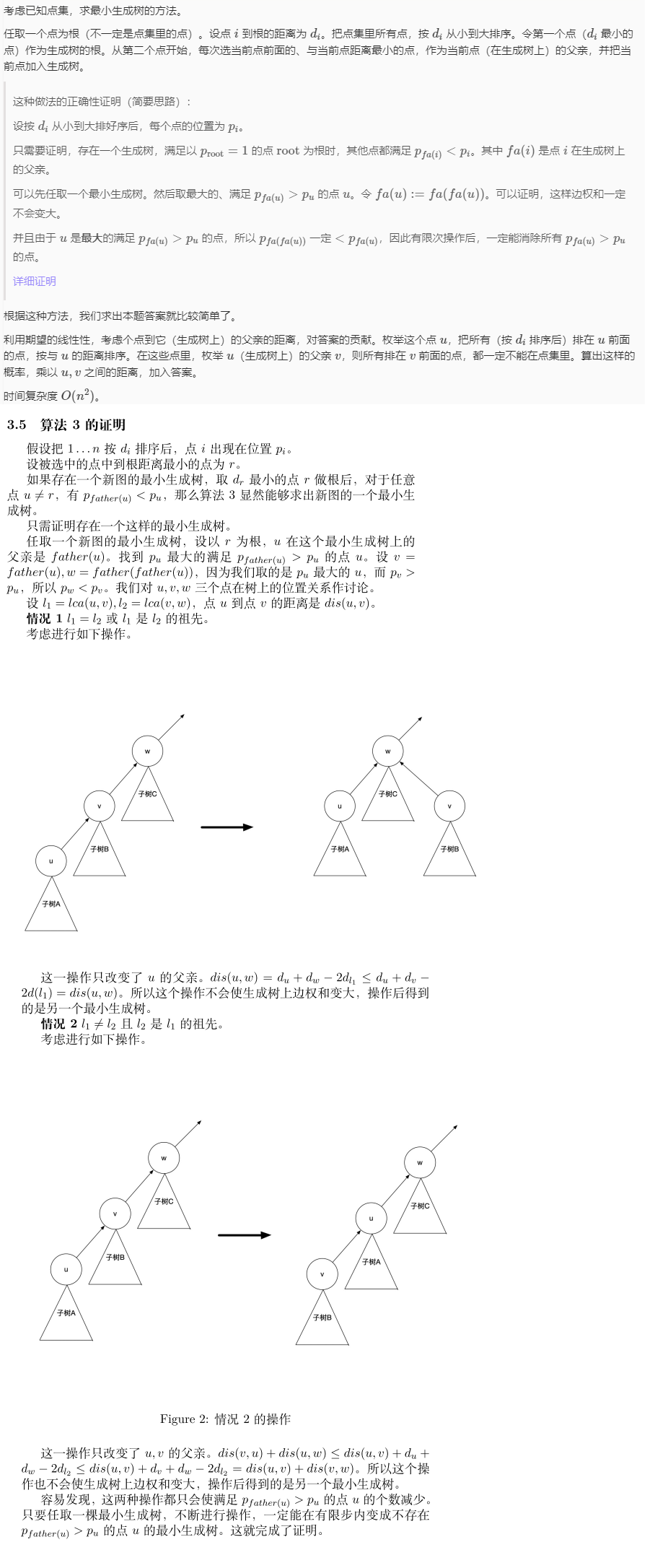
C. 硬件包管理器
你要造一套超级计算机. 为了使它的计算速度达到能够用暴力算法在瞬间内通过这场比赛的所有测试点, 你还需要在这台超级计算机上安装 $n$ 个硬件, 我们将这些硬件编号为 $1, 2, \ldots , n$. 第 $i$ 个硬件的预定安装时间是 $t_i$, 硬件之间有依赖关系. 安装硬件的时间可以忽略不计, 但是每个硬件安装的时间有一些大小限制. 一共有 $m$ 组限制, 第 $i$ 组限制可以用两个正整数 $l_i, r_i$ 表示 ($1\le l_i\le r_i\le n$), 具体意义是编号在 $[l_i, r_i)$ 的硬件的安装依赖于第 $r_i$ 个硬件的安装, 因此它们的安装时间不早于编号为 $r_i$ 的硬件的安装时间(安装时间可以相等).
所以你会发现, 完全按照预定的安装时间安装每个硬件, 这 $n$ 组限制不会全满足. 因此你要调整这些硬件的安装时间. 而你希望每个硬件的实际安装时间与预定安装时间的总偏离程度最小. 对于第 $i$ 个硬件, 如果它的实际安装时间比预定安装时间早, 那么每个单位时间都会使总偏离程度增加 $a_i$; 如果它的实际安装时间比预定安装时间晚, 那么每个单位时间都会使总偏离程度增加 $b_i$. 现在你的任务就是计算出总偏离程度的最小值.
$n, m\le 300000$
重新调整这些区间, 若 $l_i<l_j<r_i<r_j$, 那么显然 $[l_i, l_j]$ 的位置也是受 $r_j$ 约束的, 考虑把每个区间都先如此处理成极长的, 那么发现一个重要性质就是区间没有相交只有包含. 于是可以以树的形式考虑, 子节点要不早于父节点安装时间, 那就简单了, $f_{u, i}$ 表示 $u$ 的安装时间为 $i$ 的情况下 $u$ 子树的答案, 则 $f_{u, i}=\sum_v \min_{j\ge i} f_{v, j}+cost(u, i)$, 其中 $cost$ 是加两个一次函数, 然后是满足下凸+维护差分的经典trick了.
D. 历史研究
给定平面上 $n$ 个点, 求用 $m$ 种颜色染色的方案数, 满足同色的点可以用一个边长为 $K$ 的平行坐标轴的正方形包含.
$n\le 4000, m\le 3$
$m=2$ 时, 考虑所有点的包围盒, 那么一定是两个正方形卡在两个包围盒的对角上, 分别计算方案数减去两种情况都有的方案数, 复杂度 $O(n)$
$m=3$ 时先排除某一维极差 $\le K$ 的情况, 此时四个方向上边界的点有 $4$ 个, 至少有两个同色, 且不是对边的两个, 设是最左和最下的两点, 那么这个颜色的包围盒确定了, 去掉这种颜色后剩下的点的包围盒的右边和上边也确定了, 于是枚举左下两边用 $m=2$ 的方法算.
NOI2024省选模拟赛13
A. 过路费
某国共有 $n$ 座城市, 有 $m$ 条高速公路连接这些城市, 每条高速公路只能单向通行.
第 $i$ 条高速公路的起点城市是 $u$, 终点城市是 $v$, 经过一次需要 $w_g$ 的费用.
节假日到了, 国家决定对高速公路通行费进行减免, 政策如下:
- 如果一条路线经过的高速公路不超过 $k$ 条, 将按照原价收取费用.
- 如果一条路线经过的高速公路超过 $k$ 条, 将只收取其中费用最高的 $k$ 条高速公路的费用.
求从城市 $s$ 到城市 $t$ 的最小花费.
$n, m\le 1000$
这题以前见过啊
就是考虑枚举最短路上第 $k$ 大的边权值 $x$, 那么把所有边权 $w\coloneqq \max (w-x, 0)$, 最后答案加上 $kx$, 则如果 $x$ 枚举大了减的就少了, 枚举小了最后就加多了, 所以只有当 $x$ 是正确的值的时候是对的.
[think] 有一种wqs二分的感觉.
B. 数列重排
定义一个数列区间的mex为区间中最小的没有出现过的自然数, 定义一个数列的价值为其中 $mex \geq k$ 的区间数量.
给定 $n$ 个小于 $m$ 的自然数和一个区间 $[l, r]$, 令 $f(k)$ 表示 $n$ 个数构成的数列所有重排列中数列价值的最大值, 对于每一个 $k \in {l, l+1, . .. , r}$, 求出 $f(k)$. 令 $a$ 表示数字 $i$ 出现的次数, 保证存在正整数 $X$, 使得 $V<m$, $a_i \in {X, X+1}$.
先假设 $a_i=0$, 考虑对于某个固定的 $k$, 打一个大表发现则最优状态一定是 $0\ldots k$ 的循环的基础上插入其余的数, 于是就成了一个插入数的最优化问题而非构造题. 把 $\le k$ 的数称为 $A$ 类数, 有 $n$ 个, 剩余的数为 $B$ 类数.
发现一个重要的性质是把 $A$ 按 $k$ 为大小分块成 $l$ 块后所有的 $B$ 都可以插入到块间的空隙而不插入到块之内, 因为考虑若在 $i$ 插入了一个 $B$, 则右边第一个 $B$ 插入到 $i+k+1$ 一定不优于 $i+k$, 则选定一个位置的 $B$ 之后其他的都可以和它在模 $k$ 的意义下相等, 又发现开头对齐更优, 因为反正 $1\ldots c(c<k)$ 这一段不能和第一个 $B$ 构成合法区间.
于是分块后设第 $i$ 个缝隙插入有 $c_i$ 个 $B$, $A\to A$ 的贡献和没有 $B$ 的时候一样, 也就是选择长度 $\ge k$ 的区间的方案数, $B\to B$ 的贡献是 $\dfrac{1}{2}((\sum c_i)^2-\sum c_i^2)$, $A\to B$ 的部分则是
$$
(c_1+c_{l+1})(n-k+1)+\sum_{i=2}^{l} c_i(n-2k+2)
$$
数据范围太大不像dp, 考虑贪心, 先加上 $A\to A$ 的贡献和 $(\sum c_i)^2$, 考虑在当前基础上新加入一个元素, 插入到第 $1$ 和 $l+1$ 个缝隙的贡献是 $n-k+\dfrac{1}{2}-c_i$, 插入到其他位置是 $n-2k+\dfrac{3}{2}-c_i$, 显然差分递减原函数凸性, 每次取最大的差分就是对的, 所以一定是先在 $1, l+1$ 轮流插入, 直到贡献相等, 也就是两边插入了 $k-1$ 个之后每个缝隙轮着插入, 贡献都是等差数列求和, 求单个 $f(k)$ 就是 $O(1)$ 了.
总复杂度 $O(m)$
C. 构造矩阵
给定 $n, k$, 构造一个只含有 $0, 1$ 的大小为 $T \times r$ 的矩阵 $A$, 满足:
- $A_{i, i} = 1$
- $A_{i, i+1} = 1$
- 若 $i>j$, 则 $A_{i, j} = 0$
- 若 $A_{i, j} = 1$ 且 $j-i >1$, 则存在 $i<t<j$ 满足 $A_{i, t} = A_{t, i} = 1$.
- 若 $i\le j$, 则 $(A^k)_{i, j} > 0$
输出满足 $A_{i, j}=1$ 且 $j-i>1$ 的每个 $(i, j)$, 设这样的 $(i, j)$ 有 $m$ 个.
若输出不满足要求则不得分, 否则根据 $m$ 进行评分. (如图, 要求 $m\le f(k)n$)
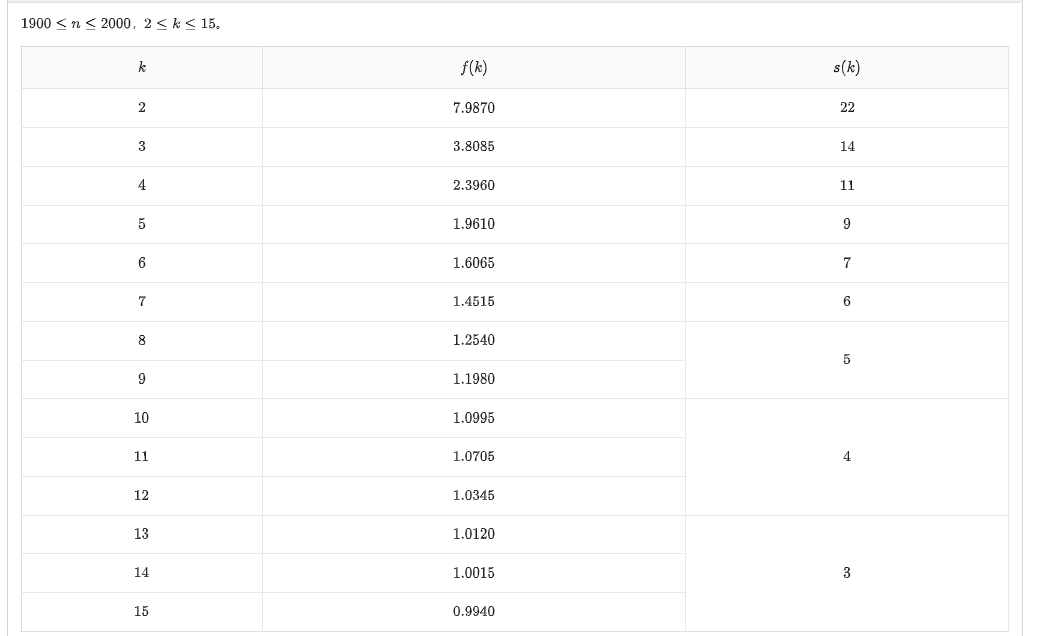
先转换成, 给定一个序列, 你有 $[i, i+1)$ 的区间, 要求进行 $m$ 次合并的预处理使得任意区间可通过至多 $k$ 次合并得到.
对于 $k=2$ 考虑猫树分治, $m=n\log n$, 对 $k=3$ 考虑sqrt tree, 将序列分治成 $\sqrt n$ 大小的块, 合并出每个块的区间和前后缀, 块内递归. $m(n)=\sqrt nm(\sqrt n)+O(n)=n\log \log n$, 对 $k=4$ 考虑递归分治, 块内递归, 块间用 $k=2$ 并处理前后缀.
于是对更大的 $k$ 就可以类比刚才的, 对序列分块块内递归, 块间递归到 $k-2$ 的子问题并预处理前后缀, 可以dp求块大小. 同时这个策略在 $k$ 大 $m$ 小的时候比较劣, 此时底层直接用线段树上层用上面的方法.
但还是不够优秀, 把块分类, 问题 $f(k, n), f_1(k, n), f_2(k, n)$ 表示查询时序列长 $n$ 可以合并 $k$ 次时的代价, 在此基础上要求查前或后缀只能用一个区间的代价, 在此基础上要求查前和后缀只用一个区间的代价, 则 $f(k, n)$ 可以分成两个边界块和中间的若干块, 两个边界块都是递归到 $f_1(k)$, 中间块要递归到 $f_2(k)$, 而若中间分了 $B$ 块又要把这 $B$ 块合并, 所以 $f(k, n)=\min_i \min_j 2f_1(i)+\dfrac{n-2i}{j}f_2(j)+f(\dfrac{n-2i}{j})$, $f_1(k, n)=n-1+f(k, n-1), f_2(k, n)=2n-3+f(k, n-2)$, 要多开一个 $g$ 优化一下 $f$ 的转移. dp的时候记录状态根据状态构造即可.
边界要处理 $i=1$ 时的 $f, f_1, f_2$, $j=1$ 时用猫树分治, $j=0$ 时处理出所有子区间, $i\le j$ 时的 $f$. 感觉很厉害的一点是它真的卡掉了dp中的小错, 那种答案只差 $1$ 的小错.
NOI2024省选模拟赛14
A. 998244o5o
原题 CF788D 3000*蓝题
二维平面上有共 $n+m$ 条未知的平行于坐标轴的直线.
你每次可以询问一个平面上点, 交互库将返回该点与离它最近的直线之间的距离.
你要在 $3 \times 10^5$ 次询问内确定这 $n$ 条直线.
题目保证直线 $x=a$ 或者 $y=a$ 中 $\vert a\vert \le 10^{8}$, 你询问的点坐标也要在 $[-10^8, 10^8]$ 中, 其中 $n, m \leq 10^4$.
曼哈顿距离在两维是对称的, 发现当问 $(x_0, y_0)$ 时, 一条 $x=x_0+k$ 和 $y=y_0+k$ 的直线是等价的, 所以这其实是个一维问题/xia, 可以都转化到与 $y=x$ 的交点.
于是考虑一维怎么做, 要保证 $O(1)$ 次问出一条线, 感觉这里分治是应该枚举的策略, 或者是考虑若已经知道 $x=l, x=r$ 两条线存在, 则这个区间要想有线 $x=mid$ 一定能问出来, 然后递归下去, 就可以线性得到一堆 $k$ 满足存在线使得 $x=k$ 或 $y=k$, 最后找一个集合之外的 $t$ 对每条线判断线的方向即可.
B. 告别
给定 $n$ 点树, 有一个路径集合 $S$, 定义一条边的权值为 $S$ 中不经过它的路径的权值集合的 $mex$. $q$ 次加入一条路径或查询经过一条边的权值的最小值.
$n, q\le 10^5$, 3s, 256Mb
套路题吧, 看见mex考虑判定或者转化成不存在的最小值, 考虑判定就会发现最小值就是最小的 $z$ 满足权值为 $z$ 的路径的交和查询路径有交, 于是考虑如何判定交, 容易想到转化成链加链求和.
然后想了一个树套树空间 $n\log^2 n$ 时间 $n\log^3 n$ 不敢写, 想了一个分块空间 $n\sqrt n时间$ n\sqrt n\log n $.
然而这就是正解.
然后可以线段树套可删堆直接维护覆盖一个点的最小颜色.
C. 被猫猫入侵的题面
原题是 Qoj4896 Alice、Bob 与 DFS
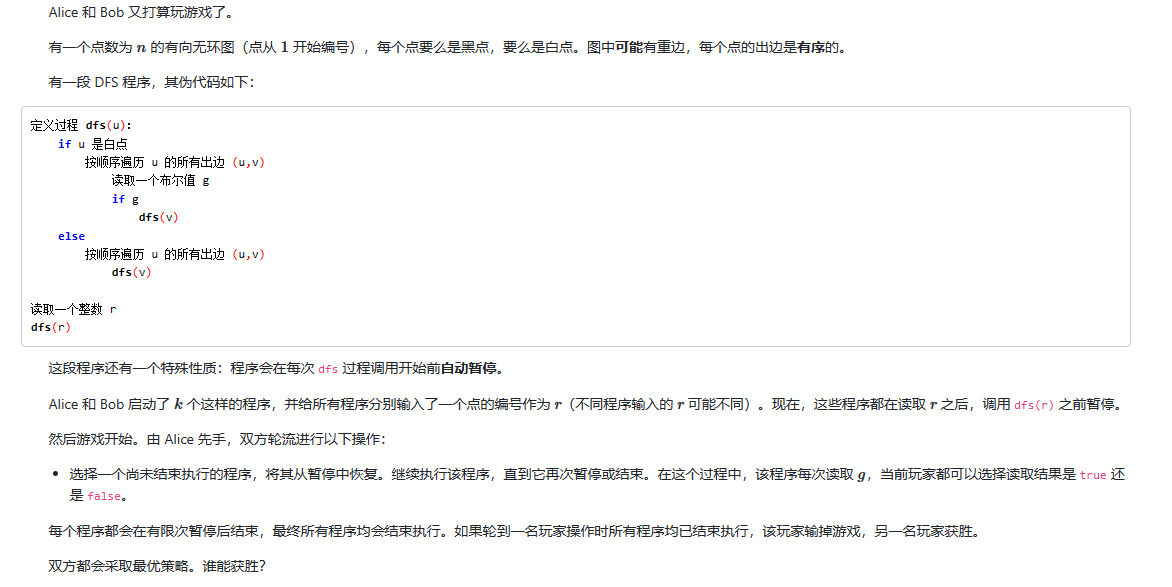
$ n\le 2\times 10^5 $
多个公平游戏, 考虑算SG, 因为是DAG所以一个状态要用$(u, {s_n}, i)$表示, 其中$ u $为当前点,$ s $为起点到当前点的路径,$ i $为走完了前$ i $条边. 设$ u $的第$ i $条边连到$ e_{u, i} $
考虑全都是白点的状态$ s $的转移,$(u, {s_n}, i)\to (e_{u, i}, {s_n}+e_{u, i}, 0), (u, {s_n}, i)\to (u, {s_n}, i+1), (u, {s_n}, i)\to (s_{n-1}, {s_{n-1}}, i’)$, 设可以转移到子树外的集合是$ S_s $, 此时SG值为$ f_{u, S_s} $.
那么就要向$ S $中加入孩子然后求$ mex $, 则倒序枚举孩子$ v $, 加入$ f_{v, S} $, 然后$ S\coloneqq S\cup {f_{v, s}} $. 然后, 发现不了考虑$ f $的过程是对$ S $不断取mex猜测$ f_{u, S}=\mathrm{mex}^{f_{u, {0}}} S $, 其中$ \mathrm{mex}^k $表示第$ k $小的不在集合中的数, 证明可以归纳.
有了黑点之后, 经过倒序枚举的第一个儿子后黑点的$ S $大小一定是$ 1 $, 信息量只有一个$ 01 $, 可以直接不断带入算出一个黑点的$ f_{u, {0/1}} $, 但是对黑点的依赖会让刚才的白点计算方式不行, 同样发现不了$ f_{u, S}=\mathrm{mex}^{f_{u, S\cap {0, 1}}}(S-{0, 1})$
最后有了以上发现不了的结论后, 就只用记录$ f_{u, S}, S\subset {0, 1} $, 然后用什么随便数据结构支持求$ \mathrm{mex}^k $就行了.
凸性在最优化问题中的应用
P6893 [ICPC2014 WF] Buffed Buffet
自助餐厅里有$ n $种食物, 分为两大类, 为 “离散食物”和”连续食物”. 你可以通过吃食物来获得收益.
离散食物用$(w, t_0, \Delta t)$描述. 对于这种食物, 你只能吃整数个, 每个重为$ w $. 吃的第一个收益为$ t_0 $, 后面每吃一个收益减少$ \Delta t $. 具体的, 吃的第$ i $个这种食物 (从$ 1 $开始标号), 收益为$ t_0-(i-1)\Delta t $.
连续食物用$(t_0, \Delta t)$描述. 对于这种食物, 你可以吃任意食物的重量. 如果你吃的重量为$ w $, 获得的收益是$ t_0w-\dfrac{1}{2}\Delta t w^2 $.
你现在要吃重量和恰好为$ W $的食物. 最大化你的收益.
$ n\le 250, W\le 10000 $.
对于离散食物, 满足$ 1\le w\le 10000 $.
对于所有食物, 满足$ 0\le t_0, t\le 10000 $.
考虑先对连续和离散分别求答案然后合并, 那么连续部分可以直接贪心, 每次选择一段直到两种食物收益(导数)相等, 相等之后两种食物选择的比例一定可以直接合并成一个.
对于离散部分对每个$ w $会拆到剩下$ \dfrac{W}{w} $个物品, 一共$ W\ln n $, 复杂度$ W^2\ln n $的3s也冲过去了.
我们知道多重背包可以$ nW $, 类似的进行优化,$ f_{i, j}=f_{i-1, j-kw_i}+kt_i-\dfrac{1}{2}\Delta t_ik(k-1)$, 类似多重背包按余数分类,$ j’=\dfrac{j}{w_i} $, 有
$ f_{i, j}=f_{i-1, k}+(j-k)t_i-\dfrac{1}{2}\Delta t_i(j-k)(j-k-1)$, 于是斜率优化, 复杂度$ nW $
P3347 [ZJOI2015] 醉熏熏的幻想乡
考虑有源汇二分图上的流. 源到左侧第$ i $个点的流量上限为$ c_i $, 且流量为$ x $(实数)时会产生$ a_ix^2+b_ix $的费用; 右侧点$ i $到汇的流量上限为$ d_i $. 求最小费用最大流.
单侧点数$ 100 $, 值域$ 3 $, 需求精确解
先求最大流.
然后考虑如果不考虑右侧点对左侧点的容量限制, 一定是贪心的选导数, 也就是存在一个$ k $使得每个左侧点的流量$ x $为$ 2a_ix+b_i\le k $的$ x $最大值. 可以想象维护了一个当前导数最小元素的集合, 随着$ k $增加增加在集合不变的情况下$ x $是$ k $的一次函数, 可能会若干次加入元素$(k\ge b)$, 删除元素(流量达到$ c_i $或受右边点限制), 形成一个分$ O(n)$段一次函数.
那么考虑怎么求流量对$ k $的函数, 发现一个性质是以$ k=1, 2, 3 $为断点的情况下每一段集合元素只会减少也就是有凸性. 因为对于一个确定的$ k $可以真的跑一遍网络流求出流量, 那么可以分治, 当前要确定函数在$ k\in [l, r]$的部分, 先计算$ l, r, mid $处的函数值, 如果三个点共线那么这就是一整段, 否则就递归下去.
UOJ455雪灾与外卖, 2018ICPC-Final正式赛 征服世界
之前已经见过了模拟费用流的做法
然而这两个题都可以直接dp, 雪灾就设$ f_{i, j} $表示前$ i $个点最后一条边的容量为$ j $(正负表示方向), 征服世界的就是改成子树, 然后转移就是做闵和, 平移, 整体加绝对值, 就是维护差分题的模板了.
Gym 102331 J J. Jiry Matchings
给定一棵$ n $个点的树, 边上带权. 对每个$ k $, 求恰有$ k $条边的最大权匹配.
$ n \le 2 \times 10^5 $
直接dp,$ f_{u, 0/1, i} $表示$ u $的子树根不能匹配/可以匹配的情况下选了$ i $条边, 则它关于$ i $是凸的, 因为我们知道二分图最大权匹配是网络流的. 于是合并是闵和.
但刚才那种维护差分的方式不好用了, 不止一个数组导致会有两个数组卷起来再取min之类的东西很那做到log以内合并, 考虑如果是链上的问题可以分治, 维护$ f_{0/1, 0/1}(i)$表示左右端点的情况, 对于$[l, r]$的答案, 求出$[l, mid], [mid+1, r]$的答案, 然后$ O(len)$的合并, 总合并复杂度就是$ n\log n $了.
于是对于树上也希望找到一种分治, 而且要求每个块和外界的点只有$ O(1)$个, 于是树剖, 先把轻儿子都合并到重链上再对重链用序列的方法, 对一个点的轻儿子合并时分治, 对重链序列分治, 复杂度就是$ n\log^2 n $了, 如果把树剖改成静态lct的方式就可以单log了.
P6731 [WC2020] 选课
经简化相当于求
$ n $个物品, 有重量$ w_i \le 3 $和代价$ c_i $. 对每个$ k $, 求恰好选重量为$ k $的物品最少花费的代价.
$ n \le 5 \times 10^5 $
[trick] 结论, 对于重量最大为$ w $的背包模$ w! $同余的位置是凸的.
于是相当于维护$ 3! $个凸包, 每次给它$ \min+ $卷上一个线段.
AGC045F
todo
P5470 [NOI2019] 序列
模拟费用流, 显然可以建图
$ s\stackrel{1, a_i}{\longrightarrow} i $,
$ i’ \stackrel{1, b_i}{\longrightarrow} t $,
$ i\stackrel{1, 0}{\longrightarrow} i’$,
$ i \stackrel{1, 0}{\longrightarrow} x $,
$ x \stackrel{K-L, 0}{\longrightarrow} y $,
$ y \stackrel{1, 0}{\longrightarrow} i’$.
然后找增广路, 显然会先走情况1$ s\to i\to x\to y\to j’\to t $, 情况2$ s\to i\to i’\to t $就是直接匹配, 此外走反悔边的可以是情况3$ s\to i\to x\to j\to j’\to t $, 相当于选择一个$ a_j $去匹配$ b_j $并把腾出来的空给$ i $, 与此对应的增广路是$ s\to i\to i’\to y\to j’\to t $. 此外还可以情况4$ s\to i\to i’\to y\to x\to j\to j’$, 腾出一个$ xy $流量并让$ a_i, a_j $直接匹配$ b_i, b_j $.
最后可能的是$ s\to i\to i’\to y\to j’\to j\to x\to k\to k’\to t $, 但这个其实是走2+4, 所以没有用.
于是开5个堆维护即可.
CF1229F Mateusz and Escape Room
contest records ZSTEST230831 C的原题
Gym 102331 H. Honorable Mention
给定长度为$ n $的序列$ a $.$ q $次查询$ l, r, k $, 求$ a_{l\ldots r} $中$ k $个不交非空子段和的最大值.
$ n, q, a_i \le 3. 5 \times 10^4 $
很厉害的题啊
考虑这个子段和关于$ k $是凸的.
如果询问全局, 可以考虑分治, 维护$ f_{u, 0/1/2/3} $区间$ u $和左右是否接通的情况下选出的子段和, 直接分治合并就是单log.
然后现在区间询问, 考虑拆成$ \log n $个区间要求它们闵和的单点, 注意到两个凸包上闵和的斜率为$ k $的位置的值就等于两个凸包各自斜率为$ k $位置的值的和, 所以只拿这些值去合并, 同时维护段数, 复杂度是二分之后在$ \log n $个区间上要lowerbound查斜率为$ k $的位置,$ n\log^3 n $了.
可以离线后整体二分砍掉一个在段上二分的log.
How to Create a Good Game Aizu - 2230
给一个DAG, 要求修改边权使得最大化边权且$ 1\to n $的最长路不变.
$ n\le 100, m\le 1000 $
先求出最长路设为$ L $, 然后开始写线性规划, 则
$$
\max \sum_{i}f_i, \
s. t. \
d_{v_i}-d_{u_i}-f_i\ge e_i\
d_1-d_n\ge -L
$$
直接对偶原问题, 可以得到
$$
\min \sum_{i}x_ie_i-Ly\
s. t. \
x_i\ge 1\
\forall u\ne 1, \sum_{i\in in(u)}x_i-\sum_{i\in out(u)}x_i= 0\
\sum_{i\in out(1)}x_i=y\
\sum_{i\in in(n)}x_i=y
$$
这就直接有源汇上下界最小费用可行流的形式了,$ u\to v $连流量$[1, inf]$费用$ e_i $的边,$ s\to 1 $连费用为$ -L $的即可.
P6631 [ZJOI2020] 序列
有一个长度为$ n $的非负整数序列$ a_1, a_2, \cdots, a_n $. 每一步你可以从以下三种操作中选择一种执行:
选择一个区间$[l, r]$, 将下标在这个区间里的所有数都减$ 1 $.
选择一个区间$[l, r]$, 将下标在这个区间里且下标为奇数的所有数都减$ 1 $.
选择一个区间$[l, r]$, 将下标在这个区间里且下标为偶数的所有数都减$ 1 $.
求最少需要多少步才能将序列中的所有数都变成$ 0 $.
对于 100% 的数据,$ 1 \leq n \leq 100000, 0 \leq ai \leq 10^9, 1 \leq T \leq 10 $.
写成线性规划, 给原来每个可能的操作一个系数$ x_i $, 要求$ \min x_i \ s. t. \ \sum_{i\in S_k}x_i\ge a_i, -\sum_{i\in S_k}\ge -a_i $. 其中$ S_k $表示操作$ k $影响的点.
对偶, 就是$ \max x_i a_i - y_i a_i $满足$ \sum_{i\in S_k} (x_i-y_i)\le 1 $, 另$ z_i=x_i-y_i $, 就成了给每个位置一个系数$ z_i $(可以为负), 最大化$ z_ia_i $, 要求每个操作对应的系数和不大于$ 1 $.
那么直接dp, 设$ f_{i, j, k, l} $表示前$ i $个点, 以$ i $为结尾的区间的和最大值分别为多少,$ j, k, l\le 1 $是显然的, 并且考虑后面影响的时候如果$ j, k, l<0 $则就相当于$ =0 $, 于是$ j, k, l\in [0, 1]$, 于是$ z_i\in [-1, 1]$, dp即可.
XX Open Cup, Grand Prix of Tokyo Evacuation
$[0, n+1]$的线段, 给定$ a_0\ldots a_{n+1} $表示这个位置洞的大小, 有$ S $个老鼠一开始在某个未知的位置$ x $有$ S $个人,$ q $次询问对于给定的$ l, r $, 另所有老鼠进洞或走出区间的最小代价的最大值. 走一步代价为$ 1 $.
$ n\le 2\times 10^5 $
考虑若对于区间$[l, r]$,$ i $离$ l $更进那么其实右边界就没用了, 所以可以设$ f_{l, r}, g_{l, r} $表示当前在$ l/r $, 走出区间的另一边或进洞的最小代价. 下面只考虑$ f $表示当前在区间最左边.
发现$ f $可以预处理$ a $的前缀和之后$ O(1)$算
同时发现有$ f_{l, r-1}+f_{l+1, r}\le f_{l+1, r-1}+f_{l, r} $, 要求$ \min_{i=l}^r f_{i, r} $, 于是建线段树把区间拆成$ \log n $个, 区间内右端点排序后就可以上分治做了.
NOI2024省选模拟赛15
A. 吴冬拔铲雪
给定$ n $个点的树, 求有多少个区间$[l, r]$满足编号在区间内的点的导出子图连通块数不大于$ m $.
$ n\le 5\times 10^5, m\le 7 $
简单题, 连通块数是点数减边数, 扫描线线段树维护前$ m $小即可.
B. 吴冬拔寻宝
给定$ n $点树, 宝藏以均匀概率位于某个点上, 每次随机一个没问过的点问出它到宝藏距离, 求确定宝藏位置的期望次数.
$ n\le 400 $
以宝藏为根, 注意到询问点集$ S $相当于询问虚树根到宝藏的距离, 则枚举虚树根$ u $算方案数即可, 要求是$ u $子树中到$ u $的距离和根相同的点所在子树必须有被选点, 且$ u $为点集虚树, 直接背包合并即可. 加上枚举根总复杂度$ n^3 $
C. 吴冬拔跳广场舞
给定长$ m $的01串$ x $, 求有多少个长$ n $的01串$ S $满足不存在连续的长$ k $的子串的$ 01 $数量相等.
$ n\le 114 $
NOI2024省选模拟赛16
A. 数排列
见 2021省队集训-模拟 Day1T1
B. 梦魇
数$ n\times m\times k $的三维空间中从起点$(a, b, c)$出发走$ d $步的方案数.
$ n, m, k\le 10^5 $
注意到三维独立, 求一维的然后卷起来.
对于一维是众所周知的反射容斥, 类似之前Day11的D, 但是那个是对所有限制求和而这次是要对步数求和. 则对于$ n< \sqrt d $可以直接dp, 对于$ n>\sqrt d $用反射容斥可以表示成$ \dfrac{d}{n}<\sqrt d $个组合数之和, 随着$ d $增加用组合数的递推式维护, 最后复杂度$ d\sqrt d $.
C. Homura V. S. Sayaka
$ n $点的树,$ m $条非树边, A追B, 开始时分别位于$(a, b)$, B先手, 每次可以走一条树边或一条非树边, A只能走树边, 问有多少不同的$ a, b $对使得A不可能追上B.
$ n, m\le 10^5 $
考虑B赢一定是B走到一条跨过$ \ge 2 $个点的非树边的一端, 则把跨过$ \ge 2 $个点的非树边标记为B的必胜点, 对于只跨过一个点的边则对树的结构影响很小, 特判即可, 而B能走到某个点的前提是到B的距离小于A的距离, 统计这样性质的点对考虑点分治, 则对于当前分治中心, 设$ a, b $之间离$ a $最近的点$ c $使得删去$ c $后$ a $的连通块里有标记点, 分为$ c, a $在分治中心一侧和$ b, c $在一侧的情况讨论.
NOI2024省选模拟赛17
原题见sdsj 2021
C. Enigma
hard
NOI2024省选模拟赛18
A. 掉落

$ n\le 10^5, w\le 10^5, h\le 10^9 $
不用动脑子的方法是kdt, 相当于从上到下扫描板子, 要支持单点加, 矩形和, 矩形赋值为$ 0 $.
更好的方法是线段树套堆, 注意到总点数(带权)只有$ O(n+w)$个, 所以线段树维护横坐标, 开小根堆维护纵坐标, 每次找到第一个根内元素最小值小于$ u_i+s_i $的暴力删点复杂度即是单log.
KDT要卡常, 方法是如果当前矩形和为$ 0 $就跳过求和/赋值为0.
B. 原神
$ n $点树, 初始$ 1 $号点为根, AB博弈, 每个点上有棋子, 每次可以把棋子移动到所在节点的子树内任意一点, 不能操作为负.
$ q $次操作每次给一条链加一个棋子, 给子树内的所有点都加一个棋子, 换根.
每次操作输出SG值.
$ n, q\le 2\times 10^5 $
先注意到一个点的SG值是最长链长度. 此外因为SG值是异或所以相当于区间翻转点的状态.
此时一种做法是先以$ 1 $为根, 考虑以点$ x $为根的时候, 除了点$ 1 $到$ x $上的点以外都和以$ 1 $为根时相同, 而这条链上的点每个点的值都是以自己(子树包含$ x $的儿子)为根时的答案, 树剖, 则大多数点这个儿子都是重儿子.
另一种的做法是考虑直径的中点, 发现只有直径中点到当前根的路径答案是到除了最远点的子树的次远点, 其他点直接是到自己最远点的距离, 所以换根切换就是修改一条链上的权值.
C. 区间mex快速算法

$ n, q\le 3\times 10^5 $
显然$(\prod a_i)\times \mathrm{mex} a_i=0 $.
在线做, 先用颜色段均摊解决掉若$ x\notin S, x\in S $, 然后线段树套可删堆维护集合中没出现的元素, 即某个$ S_i $的$ \mathrm{mex} $就是叶子到根上的最小值, 于是维护子树最小值即可求区间mex的min, 标记维护最小值加, 因此要维护最小值个数.
写的时候要保证所有删节点的区间都是被添加的, 更确切的说, 要保证若要删除某个区间$[l, r]$必然曾经添加过$[l, r]$, 而不能是$[l, p], [p+1, r]$并起来.
计数与数学
CF1392I Kevin and Grid
给定两个序列$ a_n, b_n $, 构造一张网格图, 每个点上$(i, j)$写着$ a_i+bj $.
对于一个给定阈值$ x $, 将图分为$ a_i+b_j\leq x $和$ a_i+b_j\geq x $两组连通块. 定义一个能够连通到网格图边界的连通块的价值为$ 1 $, 否则为$ 2 $. 有$ q $次查询, 每次给定$ x $, 求两组连通块各自价值之和的差.
$ n, q, a_i, b_ii, x \leq 10^5 $.
考虑对于平面图的一个连通块有$ V-E+F=1 $(不考虑外面的无限区域), 则连通块数$ C=V-E+F $.
要求$ Ans=A_1+B_1-A_2-B_2 $, 其中$ A $为总连通块数,$ B $为不和边界连通的块数, 又可以转化为$ Ans=V_1-V_2-E_1+E_2+F_1-F_2+B_1-B_2 $, 而观察不到对于每个$ F_1 $的区域, 要么是四个相邻点围成的一个格子, 要么里面正好包含一个$ B_2 $的格子.
于是就可以表示成$ Ans=V_1-V_2-E_1+E_2+D_1-D_2 $, 其中$ D $表示四个相邻点围成的格子的个数. 此时$ V, E, D $都很局部, 可以直接FFT优化计数, 如$ a_i+b_j\ge x $的横着的边可以由$ \min{a_i+a_{i+1}}+b_j\ge x $的数量算,$ D $可以由$ \min(a_i, a_i+1)+\min(b_j, b_{j+1})\ge x $算. 复杂度$ n\log n+q $
飞翔的胖鸟
给定$ a, b, h $, 求
$$
\min_{\theta\in [0, \frac{\pi}{2}]}b\theta+\dfrac{ah}{\sin \theta}
$$
直接求导得$ \dfrac{b}{ah}=\dfrac{\cos \theta}{\sin^2 \theta} $, 把$ \sin^2 $换成$ 1-\cos^2 $即可.
坑:$ b=0 $
HAMILTON
给定$ L \times n $个节点的图, 分成$ L $层, 每层是$ n $个点的完全图, 相邻两层之间的$ n $对点对应连边. 求这张图的哈密顿回路数量.
$ L, n \le 500 $.
直接dp,$ f_{i, j} $表示前$ i $层最后一层向上留出$ i $段($ 2i $个端点), 每次转移要合并这些端点和新的一层的其他$ n-2i $个孤立点, 直接算把$ a $个段合并成$ b $个段只要算$ \dfrac{a! }{b! }\binom{a-1}{b-1} $(先给$ a $个版乱序再插板再除掉顺序), 但是这$ a $个段中有$ n-2i $个不能自己一段, 枚举钦点$ k $个孤立点不成段的方案即可, 总复杂度是$ n^2L $
loj6696 复读机 加强版
群里有$ k $个不同的复读机. 为了庆祝平安夜的到来, 在接下来的$ n $秒内, 它们每秒钟都会选出一位优秀的复读机进行复读. 非常滑稽的是, 一个复读机只有总共复读了$ d $的倍数次才会感到快乐. 问有多少种不同的安排方式使得所有的复读机都感到快乐.
$ n\le 10^9, k\le 5\times 10^5, d\in {1, 2, 3, 4, 6} $, 保证模数$ P $满足$ d\vert P-1 $
相当于求
$$
x^n! })^k
$$
对这种$ id $,$ d $又很小, 考虑单位根反演
$$
\sum_i [d\vert i]\dfrac{x^i}{i! }=\sum_i \dfrac{x^i}{i! } \dfrac{1}{d}\sum_{j=0}^{d-1}w_d^{ij}
=\dfrac{1}{d}\sum_{j=0}^{d-1} w_d^je^{w_dx}
$$
分类讨论, 当$ d=1 $时显然,$ d=2 $时$ w=-1 $则求$x^n^k $, 则$ e^ix $的系数显然是$ \binom{k}{\frac{k+i}{2}} $.
对于$ d=3, 4, 6 $, 其共同点是$ \varphi(x)=2 $, 这里又有结论说
[trick] 对于单位根$ w_k^0\ldots w_k^{k-1} $, 可以被其中的$ \varphi(x)$个以整系数线性表示, 于是最终会变成$ \sum_{i=0}^{d-1}e^{(c_i+d_iw)x} $的$ k $次方, 然后见到这种项数小的直接微分有限递推即可.
[trick] 求$[x^n]F^k $,$ n $很大$ k $不大$ F $项数很小的情况, 微分有限直接递推.
这个递推很好写, 因为没有的项都是$ 0 $没有奇怪的边界.
loj3626 愚蠢的在线法官
给系统一棵$ n $个点的有根树和每个点的点权$ v_i $, 且令根为节点$ 1 $, 同时传给系统一个长度为$ k $的数组$ A $, 构造阶为$ k $的方阵$ B $, 其中$ b_{i, j}=v_{LCA(A_i, A_j)} $, 即:
$$
B=\begin{bmatrix}
v_{LCA(A_1, A_1)} & v_{LCA(A_2, A_1)} & \cdots & v_{LCA(A_k, A_1)} \
v_{LCA(A_1, A_2)} & v_{LCA(A_2, A_2)} & \cdots & v_{LCA(A_k, A_2)} \
\vdots & \vdots & \ddots & \vdots \
v_{LCA(A_1, A_k)} & v_{LCA(A_2, A_k)} & \cdots & v_{LCA(A_k, A_k)}
\end{bmatrix}$$
其中$ LCA(x, y)$为节点$ x $和$ y $的最近公共祖先, 当你传入数组$ A $后, 将计算构造出来的这个方阵的行列式.$ n, k\le 5\times 10^5 $
显然$ A $是排列否则行列式为$ 0 $. 同时$ A $的顺序没有影响(交换一次行一次列答案不变), 假设它是dfs序, 因为是树的结构考虑能不能递归做.
那么因为一个子树是一个区间, 不同子树的lca全是根, 所以会把矩阵画出若干个沿对角线, 对角相接的小方阵, 每个代表一个子树, 剩下的地方全是$ v_1 $.
[trick] 若$ M’{i, j}=M{i, j}+x $, 则$ \det M’=\det M+(\sum_{i, j} A_{i, j})x $, 其中$ A_{i, j} $为$ i, j $处的代数余子式.
于是可以dp了, 设$ f_u $表示$ u $所在子树部分所有数都减去$ u $的行列式,$ g_u $表示$ u $所在子树部分的矩阵的代数余子式的和:
- 那么如果$ u $没有出现在矩阵中, 矩阵的形态是沿着对角线若干个对角相连的小方阵即每个儿子子树对应区域, 其他位置全是$ w_u $, 给所有位置都减去$ w_u $求出$ f_v $, 则$ f_u=\prod f_v+g_uw_u $,$ g_u=\sum_i g_i\prod_{j\ne i} f_j $,$ f $的转移显然,$ g $的转移是注意到子树外位置的代数余子式都是$ 0 $.
- 如果$ u $出现在矩阵中, 则第一行第一列和其他儿子子树部分之外的地方全是$ v_1 $, 用下面每一行减去第一行, 则递归成了第一行是$ w_u $, 下面除了儿子子树对应区域全是$ 0 $的问题, 有$ f_u=w_u\prod f_v, g_u=\prod f_v $, 其中$ g_u $的转移是注意到, 对于一行的代数余子式之和, 其等于把这一行都换成$ 1 $之后的矩阵求行列式, 此时和第一行全为$ w_u $的线性相关行列式为$ 0 $, 所以最后只有第一行第一列的代数余子式剩下, 即$ \prod f_v $
复杂度线性.
loj3653 抽奖机
有$ n $个$ \bmod 3 $的加法单元, 一开始这些单元为$ 0 $.
有$ m $种操作, 第$ i $种操作选择$ a $个单元$ +1 $,$ b $个单元$ +2 $(选出的两部分不交). 你要进行$ k $轮操作, 每轮选择一种操作(每轮共有$ \binom{n}{a, b} $种可能).问$ k $轮以后, 有$ i $个单元为 1,$ j $个单元为 2 的方案数.
$ n \leq 100, k \leq 10^{18}, \text{mod} = 10^9+9 $
考虑相当于对一个集合多项式做3-FWT, 每个操作可以表示为三进制下的多项式$ F_i $, 若$ S $中包含$ a_i $个$ 1 $和$ b_i $个$ 2 $则$ x^S $的系数为$ 1 $, 而最后就是要求$ G=\sum F_i $的$ \sum_{S, cnt_1=i, cnt_2=j} [x^S]G^k $
发现对于$ 1, 2 $个数相等的元素系数都是一样的, 考虑把它们压起来, 就要解决压起来的情况如何做FWT.
先回顾本来FWT-k是怎么做的:
[trick] FWT的变换都可以认为是找$ c’(S, T)$使得$[x^S]F’=\sum_T [x^T]F $, 而$ c’(S, T)$又是关于位独立的即$ c’(S, T)=\prod_i c(S_i, T_i)$. 对于FWT-k, 就有$ c_{i, j}=w_k^{ij} $, 逆运算则是$ c_{i, j}=\dfrac{1}{k}w_k^{-ij} $.
那么现在, 用$(a, b)$表示$ a $个$ 1 $,$ b $个$ 2 $,$ n-a-b $个$ 0 $的状态, 则$ c((a, b), (c, d))=\sum_T \prod_i c(S_i, T_i)$其中$ S $为任意一个满足$(a, b)$的状态而$ T $是遍历所有$(c, d)$的状态.
那么$ A=(a, b), B=(c, d), c(A, B)$重要的就是$ a $个$ 1 $对应的$ B $中元素$ 1, 2 $的个数和$ b $个$ 2 $对应的个数, 这两部部分合并是二维背包, 可以写出BGF:
$$
\begin{gathered}
c((a, b), (c, d))=[x^c y^d] (1+wx+w^2y)^a(1+w^2x+w^4)^y(1+x+y)^{n-a-b}\
let\ c(c(a, b), (c, d))=[x^c y^d]F_{a, b}(x, y)\
\therefore
F_{a, b}=F_{a-1, b}\dfrac{1+wx+w^2y}{1+x+y}
\end{gathered}
$$
于是能递推了, 推一下复杂度$ n^2 $, 总复杂度$ n^4 $
NOI2024省选模拟赛19
A. 最小四贪那树
给定$ n $点完全图,$ q $次询问一个给定子集的最小斯坦纳树.
$ n\le 21, q\le 10^5 $
先预处理$ g_{S, i} $为集合$ S $中点到点$ i $的最小距离, 再dp出$ f_S $为点集$ S $的最小生成树, 再跑FMT即可.
复杂度$ n2^n $, 然而不处理$ g $的$ n^22^n $也过了.
B. 数位
给定序列$ b_n $, 定义$ f(x)$为$ x $的十进制表示下所有位的值的权值和, 如$ f(2024)=c_2+c_0+c_2+c_4 $.
给定字符串$ a_n $包含
0-9和?, 要求把?替换成数字, 设得到的数为$ a $, 最大化$ \sum_{i=1}^n f(b_i+a)$.$ a $不能有前导$ 0 $.
很经典的trick, 在lyh dp那篇里出现过, 就是加上相同的数$ x $, 第$ i $位会进位的数一定是最低$ i-1 $位从大到小排序后的前缀.
于是设$ f_{i, j} $表示最低$ i $位, 进位的数有$ j $个即可转移, 复杂度$ 10n^2 $, 排序可以用stable_sort
C. 树与
$ q $次询问树链上选$ m $个点, 点权按位与的最大值.
$ n\le 10^6, q\le 10^5, a_i\le 2^{64} $($ a_i $是点权)
contest records KFC NOIP 2022(20221125wjw模拟赛) C. sequence CF1665E有这个题选$ 2 $个数的情况的结论.
加强结论, 考虑选$ m $个数仍然可以用相同方式归纳, 若现在试图证明对于值域为$ 2^k $下最多有$(m-1)k $个, 那么若这一位有至少$ m $个$ 1 $, 这一位一定选$ 1 $, 选到的一定是前$ k-1 $位的最大值拼上一个$ 1 $, 否则这一位最后的值是$ 0 $, 选的数可能这一位是$ 1 $则一定来自前$ k-1 $位的最大值, 再加上新增的最多$ m-1 $个这一位是$ 1 $的数.
于是有结论
[trick]: 在值域$ V $的集合$ S $中选$ m $个数最大化按位与或最小化按位或,$ m $个数一定都是最大/最小$(m-1)\lg V $个数中的数.
于是先求链上前$ m\lg V $大, 直接线段树维护多log, 考虑用ST表支持求最大, 树剖成$ \log n $个区间把区间压到堆里, 每次弹出一个区间拿出它的最大值再分裂成两个放回去. 复杂度$ qm\log V\log(m\log V)$.
然后贪心部分就是从高到低删判断数量.
在贪心过程中求前若干大而不是先求后贪可以有效卡常.
NOI2024省选模拟赛20
A. 网络单纯形
给定连通无向图$ Graph(n, m)$, 边有边权$ w_i $, 点有颜色$ c_i $,$ q $次修改一个点的颜色询问所有连通不同颜色点的边的边权最小值.
$ n, q\le 2\times 10^5 $
考虑两个颜色的答案就是给定的两个集合间的最近的一条边, 那么这条边一定在最小生成树上.
用堆维护每个点的所有儿子的信息, 修改时更新父亲节点的数据结构即可.
B. 原神账号
给定$ a_n $,$ m $次询问第$ i $次给定$ k_i $个区间和$ k_i $个区间$[l_j, r_j]$问区间并的颜色数. 强制在线. 空间8Mb.
$ n, \sum k, m\le 10^5 $
早上刚看了跳进兔子洞就开到这个题, 容易想到bitset, 问题变成如何在8Mb下提取区间bitset.
容易想到st表, 空间爆炸, 容易想到分块, 时间爆炸.
但是分块是可以调块长的! 设块长为$ B $, 每$ B $个分一块, 块间st表, 空间时间都是$ \dfrac{n^2}{Bw}\log \dfrac{n}{B} $, 取$ B=\dfrac{n}{w} $得到$ n\log w $, 过了.
C. 肖芬途
给定$ n $点树,$ 1 $为根, 有点权$ a_i $, 设$ i $的父亲为$ fa_i $, 保证$ fa_i<i, fa_i\le fa_{i+1} $.
$ q $次询问给定区间求$ \sum_{x=l}^r \sum_{y=l}^r [l\le lca(x, y)\le r]a_xa_y $
强制在线$ n, q\le 2. 5\times 10^5 $
首先容易想到$ fa $的这两个性质比较重要, 发现它是描述了像zkw线段树一样从上到下按层标号的”bfs序”.
显然考虑扫描线, 扫$ r $的话, 对当前询问区间$[l, r]$, 区间内的点的连通块的所有根也形成编号上一个区间, 而答案就是$ \sum_{rt} (\sum_{u\in subtree(rt), u\in [l, r]} a_u)^2 $, 那么只要根号重构, 维护出子树点权和在编号维上的前缀和就可以查询整块答案, 此外散块的修改可以直接求$ k $级祖先看它是哪个子树里的计算贡献.
然后强制在线就把扫描线可持久化也就是记录每个$ r=kB $时每个点的子树大小了.
NOI2024省选模拟赛21
A. 盗梦空间
给定一棵树,$ q $次给定点集$ S $, 询问树上每个点到$ S $中的点的最小距离的最大值.
$ n, \sum \vert S\vert, q\le 10^5 $
一眼虚树, 代码量略大, 对于虚树每条边, 每个子树, 虚树根外的答案都是显然的, 用了树剖加st表查虚树的边的答案.
B. 偷藏女装
小W摆放物品时有个习惯, 不喜欢打乱原先物品的位置, 因此小家的衣柜只能从两财开, 可以从左边放衣服进去也可以从右边放衣服进去, 并且会把之前已经在衣柜里的衣服往中间挤. 比如衣柜里面已经有$ 1, 2, 3 $三件衣服了, 现在从左边放一件$ 4 $号衣服进去就变成了$ 4, 1, 2, 3 $, 在右边放一件$ 5 $号衣服就变成了$ 4, 1, 2, 3, 5 $. 现在AlseoR带着机房人民集资为小A买的$ n $件衣服潜入了小A的家, 将衣服按编号从小到大放进衣柜, 每次可以任意选择左侧或者右侧放入.
但是小W作为一个强迫症, 他希望可以存在一种方式从衣柜两侧不断取出衣服((取完为止), 每次可以任意选择将左似的衣服或者右侧的取出, 第$ K $件可以取出女装. 所以他想问问你方案的总数. 由于小A不知道衣柜里面的衣股是怎么摆放的, 所以他只关心取出的顺序字. 即对于两个方案不同, 当且仅当存在一个$ x $两个方案取出的第$ x $件衣服编号是不同的. 当然这个数可能很大, 所以小A决定从他最喜欢的三个数中选一个给你当模数.
$ n, m\le 10^9 $
考虑最后取出序列满足的条件, 衣柜里是一个单谷的中间是$ 1 $, 则取出序列一定满足:
- 前$ k-1 $个元素可以被划分成两个递减序列.
-$ a_k=1 $ - 后$ n-k $个序列是一个递增序列每次取头/尾得到.
- 前$ k-1 $个元素划分出的序列中某个序列的最小值大于后$ n-k $个元素
todo
C. 楼梯调度
对于一个序列$ a_1\ldots a_m $, 其权值为$ \sum_{i=1}^m \max_{j=1}^i a_i $, 现在给定$ a_n $求把它划分成两个序列$ b, c $后两个序列最小权值和.
$ n\le 5\times 10^5 $
先上来dp, 容易想到设$ f_{i, j} $表示前$ i $个人, 让序列$ b $的前缀$ \max $是序列$ a $的前$ i $个数的最大值, 此时$ c $的前缀$ \max $是$ j $的情况下的最小代价. 转移考虑新加的数$ a_i $, 可以放到$ b $序列(设$ s_i=\max_{j=1}^i a_i $)$ f_{i, j}=f_{i-1, j}+s_i $, 可以放到$ c $序列$ f_{i, j}=f_{i-1, j}+j, \ if\ j>a_i $,$ f_{i, j}=\min_{k<j} f_{i-1, k}+a_i\ if\ j=a_i $.
发现转移只需要维护一个序列支持区间加, 区间加下标, 区间最小值, 单点修改, ktt秒了.
然后这个题里因为每次后缀加下标不影响势能, 前缀加单点修改只影响边界的log个节点, 所以可以分析到$ \log^2 $而不是$ \log^3n $
NOI2024省选模拟赛22
A. 染色问题
给定一个$ n $个点$ m $条边的联通无向图, 给图上每个点染上$ k $种颜色中的一种, 且要求每一条边的两个端点不同色(不需要使用全部$ k $种颜色). 求方案数.
$ n\le 10^5, m\le n+5 $
广义串并联图说我们直接缩一度点和二度点, 即若一个点度数为$ 1 $可以删掉然后给答案乘$ k-1 $, 如果度数为$ 2 $则设一条边$(a, b)$表示这条边两边点颜色相同时方案数为$ a $, 不同时为$ b $, 则若原来该点连的两条边分别是$(a, b), (c, d)$, 新的边应为$(ac+(k-1)bd), (ac+bd+(k-2)bd)$, 缩到最后直接枚举颜色的集合划分$ B(10)$即可.
B. IOer
小Z是一个IOer, 很快就要参加IO省选了, 他可以用来刷题的时间还剩下$ n $天. 由于IO题非常简单, 你可以认为小Z能在一天内刷完任意数量的IO题, 且每题只会考察一个知识点.
IO题的数量非常多, 你可以认为考察每个知识点的IO题都是足够多的. 在开始刷题前, 小Z只会$ v $个知识点.
在这$ m $天中, 小Z会每天学习新的知识点. 在第$ i $天开始刷题前, 小Z会学习$ u $个新知识点. 即在第$ i $天刷题时, 小Z已经掌握了$ v+ui $个不同的知识点. 只有一道题所考察的知识点已被掌握时, 小Z才能刷这道题.
虽然IO题非常简单, 但是小Z还是不能做到同时刷多道IO题, 因此小Z在同一天刷的题, 时间上存在先后顺序.
小Z想在省选前刷恰好$ o $道题. 小Z不关心题目的具体内容, 只关心题目所考察的知识点. 他想知道, 共有多少种不同的刷题方案. 两种刷题方案是不同的, 当且仅当存在$ 1<i<n $, 按时间顺序, 小Z刷第$ i $道题的时间在两个方案中不在同一天, 或小Z刷的第$ i $道题所考察的知识点不同. 但是小Z不会OI, 所以他无法求出不同的刷题方案数. 于是他找到了你, 一个能随手AK模拟赛的OIer, 希望你帮他解决这个问题.
由于答案可能很大, 你只需要回答答案模$ 998244353 $的值.
$ n\le 10^{18}, m\le 2\times 10^5, u, v\le 10^9 $
显然可以列答案的生成函数:$ ans=[z^n]\prod \dfrac{1}{1-(ui+v)x} $.
发现$ n $,$ m $都很大, 直接线性递推只能做到$ m\log m\log n $肯定不行, 此时考虑分式分解, 也就是像我们一开始求Fib数列时, 把它的生成函数拆成$ \dfrac{1}{1-cx} $的形式以得到通项的方法, 显然对于多项式$ \dfrac{p}{\prod_i q_i} $, 拆成$ \sum_i \dfrac{d_i}{q_i} $后$ d_i $的系数小于$ q_i $, 得到方程$ \sum_i\dfrac{Md_i}{q_i}=p $, 其中$ M=\prod_i q_i $,
考虑因为$ d_i $的次数小于$ q_i $, 所以$ d_i=d_i\bmod q_i $, 两边都模掉$ q_i $后, 左边只有第$ i $项不为$ 0 $, 于是得到$ \dfrac{M}{q_i}d_i\equiv p\pmod {q_i} $, 于是只要求$ p\bmod q_i $和$(\dfrac{q_i}{M})\bmod q_i $, 对于本问题$ p\bmod q_i=1\bmod q_i=1, \dfrac{q_i}{M}\bmod q_i=\dfrac{q_i}{M}[\dfrac{1}{ui+v}]=\dfrac{1}{\prod_{j\ne i}(1-\dfrac{uj+v}{ui+v})}=\dfrac{u^{1-m}(ui+v)^{m-1}}{\prod_{j\ne i}(i-j)} $(这里用方括号表示函数求值), 化成阶乘做完了.
最后复杂度$ n\log n $(快速幂).
组合意义:

C. 力脑
有一长度为$ n $的仅由
0和1构成的字符串$ s $, 某些位置的字符已经给定, 其他位置的字符等概率取0或1, 求$ s $的后缀自动机的结点数量的期望, 答案对$ 998244353 $取模.$ n\le 36 $
考虑SAM的节点数和parent tree的节点数是一样的而后者结构显然更好考虑, 那么对于字符集为$ 2 $的$ s $后缀树每个点最多有两个儿子, 设$ 0/1/2 $个儿子的数量分别为$ a, b, c $, 则分别求$ a, b, c $的期望即可. 发现叶子个数$ a=c+1 $, 于是只要求$ a, b $了.
考虑SAM的parent tree什么时候只有$ 0/1 $个儿子,$ 0 $个儿子一定是一个前缀且全串只出现一次,$ 1 $个儿子一定是一个前缀最前面加一个0/1恰好有一种在字符串中出现过.
先考虑$ a $怎么算, 一个暴力是对每个前缀单独计算$ p_i $表示$ i $前缀只出现一次的概率, 则它不能是另一个前缀的后缀, 考虑容斥它是集合$ S $中的后缀的前缀其他任意, 则可以得到若干相等关系, 把它建图计算方案数, 复杂度是$ n^22^{n-i} $($ S $中只有更长的前缀).
那如果找到一个$ 2^i $的东西就赢了, 于是可以直接枚举这个前缀到底是什么, 然后dp每个位置的容斥系数之和, 设$ f_j $表示$ j $是$ S $中最大的元素的情况下所有位置的容斥系数乘只考虑前$ j $个位置的方案数的和, 则对于$ f_j $, 首先如果$ f_j $的最后$ i $个位置无法和当前枚举的匹配显然是$ 0 $, 否则枚举当前前缀上一次出现的位置$ k $, 若$ j-k< i $则有重叠, 要求$ j-k $是一个border, 如果$ j-k\ge i $则中间没有覆盖的没确定的位置可以任选. 这个的复杂度就是$ n^22^i $
于是求$ a $的总复杂度是$ n^22^{\frac{n}{2}} $, 再考虑求$ b $, 直接算前缀加一个0出现至少一次不好算, 考虑一个点有一个儿子等价于不是叶子且它没有另一个儿子. 而没有加1得到的儿子就是在这个前缀前面加一个1不出现在字符串中, 发现正好是字符串前面添一个1然后跑刚才的做法得到的(实际上刚才求得不是恰好出现一次而是没在其他位置出现), 于是恰好只加0的儿子的概率实际上是$ p_{1, i}-p_i $, 其中$ p_{0/1, i} $表示在字符串前面添加一个字符0/1之后跑出的答案.
最终答案是$ a+b+c=2a+b-1=(\sum_i 2p_i+p_{0, i}-p_i+p_{1, i}-p_i)-1=(\sum_0 p_{1, i}+p_{1, i})-1 $.
字符串专题
失配树
给定字符串$ s_n $,$ m $次询问$ s_{1\ldots p}, s_{1\ldots q} $的最长公共border长度.
$ p, q, s\le 10^6, m\le 10^5 $
失配树说的是每个点向自己的最长border连边, 则这个题是求lca.
P4156 [WC2016] 论战捆竹竿
给定长$ n $的字符串$ S $, 有一个空串, 求每次可以将$ S $去掉一个border的部分拼上去求最后长度在$[n, w]$内有多少长度可以拼出来.
$ n\le 5\times 10^5, w\le 10^18 $
考虑就是用$ S $所有周期长度线性组合, 先求出所有周期$ a_1\ldots a_k $. 然后接下来问题是同余最短路的形式.
直接做同余最短路的转圈是$ n^2 $, 考虑优化, 有结论一个串的border构成$ \log n $个值域不交的等差数列, 那么转圈的时候一次转移一个公差为$ d $长$ n $的等差数列, 单调队列转移即可.
P4548 [CTSC2006] 歌唱王国
求字符集为$ m $的情况下,$ T $初始为空, 每次随机一个字符串追加到$ T $, 期望多少次使得$ S $为$ T $的子串.
$ \vert S\vert \le 10^7, m\le 10^9 $
列PGF, 设$ F $是还不包含$ S $的PGF,$ G $是包含$ S $的PGF.
给$ G $的情况添加整个串$ S $一定得到包含$ S $的串, 但可能加了一半就得到了, 发现此时加了一个$ S $的border, 于是就是
$$
m^{-\vert S\vert}x^{\vert S\vert}F=\sum_{i\in border(S)}Gx^{\vert S\vert -i}m^{-\vert S\vert +i}
$$
最后要求的期望步数是$ \sum f_i=F(1)$, 于是$ F(1)=\sum_{i\in border(S)} m^iG(1)$, 而$ G(1)$是最终能得到的概率之和也就是$ 1 $, 于是$ F(1)=\sum_{i\in border(S)} m^i $了.
hdu6791 Tokitsukaze, CSL and Palindrome Game
在歌唱王国的基础上, 给定字符串$ S $, 每次给定两个区间询问用上一题的方法哪个区间的答案大. 保证两个区间都是回文子串.
$ n, q\le 10^5 $
用PAM处理可以得到每个回文子串的border的若干个等差数列, 而因为等差数列值域无交,$ \sum_{i\in border(T)} m^i $的式子中没有进位, 于是只要比较border序列字典序即可.
ROI 2016 DAY2二指禅
原题! 本篇训练赛8 C. 数据结构
CF1483F EXAM
给定互不相同的字符串 $ s_1, s_2, \cdots, s_n $, 求有多少对 $(i, j)$满足:
- $ i \neq j $
- $ s_j $是 $ s_i $的子串.
- 不存在 $ k $$(k \neq i, k \neq j)$满足 $ s_j $是 $ s_k $的子串且 $ s_k $是 $ s_i $的子串.
保证 $ n, \sum \lvert s_i \rvert \leq 10^6 $.
考虑对于长的串考虑其对短串的贡献, 则对$ s_i $枚举$ s_j $的右端点位置, 显然每个右端点只有最长的是有用的, 对每个右端点$ r $处理出$ l_r $表示最小的$ l $满足$[l, r]$是某个$ s_j $, 那显然被包含的区间不能贡献, 而对于不被包含的仍然可能会错, 发现一个子串不能贡献当且仅当它在这个字符串中的每一次出现中有任意一次没有被统计成$ l_x $或者被其他区间包含, 也就是一个子串$ s_j $被贡献当且仅当其在$ s_i $的实际出现次数等于只统计不交区间$[l_r, r]$的情况下它的出现次数.
统计不交区间那个次数显然扫一遍就有了, 于是要支持查$ s_j $在$ s_i $的出现次数, 可以上一个SAM把所有串拼在一起统计子树endpos用AC自动机. 也是子树endpos个数.
CF1393E2 TWILIGHT AND ANCIENT SCROLL (HARDER VERSION)
给定$ n $个串$ {s_n} $, 在每个串中删除之多$ 1 $个字符使得$ s_n $构成字典序递增的序列, 求方案数.
$ \sum \vert s_i\vert \le 3\times 10^6 $
显然要知道上一个串选了什么, 设$ f_{i, j} $表示第$ i $个串删了第$ j $个字符情况下的方案数.
那么考虑如果当前字符串$ s_i $要删第$ j $个, 设$ s_{i-1} $删第$ k $个, 可以先求删了之后得到的$ s_i’$和$ s_{i-1} $的lcp设为$ p $.
- 对于$ k>p $的部分, 显然对$ s_{i-1}’$的前面位置没有影响, 只要$ s_{i, p+1}>s_{i-1, p+1} $即可转移.
- 对于$ k\le p $的部分, 比较$ s_{i-1}’$和$ s’_{i} $.
- 若$ s’{i-1, 1: p}=s’{i, 1: p} $则$ s’{i-1, 1: p}=s{i-1, 1: p} $, 说明$ s_{i-1} $在位置$[k, p]$全部相等, 此时在其中的删除会得到同一个字符串$ t $, 比较它和$ s’_i $即可转移这个区间.
- 否则$ s_{i-1}’$和$ s_i’$的lcp就是$ s_{i-1}’$和$ s_{i-1} $的lcp, 也是$ s_{i-1} $在位置$ k $后面第一个不等于$ s_{i-1, k} $的字符的位置减$ 1 $, 设该位置为$ p’$则要求$ s_{i-1, p’}>s_{i-1, k} $即可转移, 那么这些位置与$ j $无关, 可以直接前缀和处理出来.
最后就只有求lcp的复杂度加线性dp.
CF1276F Asterisk Substrings
给定一个字符集为小写字母的长度为$ n $的字符串$ s $, 设$ t_i $表示将$ s $中的第$ i $个字符替换为特殊字符$ \text{} $时得到的字符串, 比如当$ s=\text{abc} $时,$ t_1=\text{bc} $,$ t_2 = \text{ac} $,$ t_3 = \text{ab} $.
求字符串集合$ {s, t_1, t_2, t_3, . .. , t_n} $中本质不同的子串个数(需要计算空串).
注意$ \text{*} $仅表示一个字符, 不表示其他含义(如通配符).
$ n\le 10^5 $
不包含$ \text{} $的数量显然, 只考虑包含$ \text{} $的子串, 则这样的子串是一个子串的所有后缀拼上$ \text{} $拼上一个子串的所有前缀, 用$(a, b)$表示, 其中$ a, b $分别表示$ \text{} $前后的部分. 而字符串$ t_i $包含这个子串就是把字符串$ t_i $表示成$(x, y)$, 要求$ a $是$ x $的后缀,$ b $是$ y $的前缀.
于是对$ s $建立正反两个SAM及后缀树, 则$ a $是$ x $的后缀可以表示成$ a $是$ x $在树上的祖先, 另一边同理. 问题转化为给定两棵树, 有$ n $对$(x_i, y_i)$, 求有多少个$ a, b $满足$ a $是存在$ i $使得$ x_i $的祖先,$ b $是$ y_i $的祖先.
最后这个数数, 考虑枚举$ a $, 求它的子树中的$ x $对应的$ y $在另一棵树上的祖先的并集, 可以枚举一个$ a $给所有子树里的$ x $对应的$ y $到根路径加$ 1 $, 然后用重剖换根+全局平衡二叉树可以2log吧.
然而因为点集到根的路径的并长度是可以直接用线段树在合并过程中维护的:
[trick] 点集到根的路径的并的长度是所有点的深度减去相邻点lca的深度.
ICPC 2021 沈阳 M STRING PROBLEM
给定串$ S $求每个前缀字典序最大的子串.
$ \vert S\vert \le 10^6 $
建SAM, 插入过程中维护转移每次走最大的那条链.
另一种方法是, 注意到答案一定当前前缀的一个后缀, 于是新增一个字符新的答案是当前答案的border加新字符.
P5420 [CTSC2016] 香山的树
定义一个串是好的当且仅当它是自己唯一最小的循环同构.
对所有长度$ \le n $由小写字母构成的串$ S $查询一个串在好的串中的rank或者kth.
$ n\le 50, k\le 10^{18} $
求kth也是求rank. 考虑如果是让计数所有lyndon word就是没有整周期的串除以$ n $, 因为其所有循环互不相同恰有一个是最小的.
那考虑现在要计数大于字符串$ t $的$ s $的个数, 仍然假装$ s $无循环节, 考虑枚举两个字符串的LCP是$ p $, 那么就要求$ s $的循环同构都比$ t $大, 也就是$ s $任意长度为$ \vert p\vert $的子串都不比$ p $的字典序小, 且不能出现$ t $比$ \vert p\vert $更长的前缀. 注意若串中出现了$ k $次子串$ p $, 则它会被算$ k $次, 于是贡献$ \dfrac{1}{k} $
于是可以dp了, 设$ f_{i, j, k} $表示以$ p $为前缀, 长度为$ i $, 当前kmp自动机上节点为$ j $, 且到当前位置$ s $中有$ k $个子串$ p $的方案数, 直接dp转移$ O(1)$复杂度$ n^3\vert \sigma\vert $再加上一开始枚举每一位二分就是$ n^4\vert \sigma\vert\log {\vert \sigma\vert} $
NOI2024省选模拟赛23
A. 星际逃亡
有$ n $个三维空间中的星球, 第$ i $个一开始位于$(x_i, y_i, z_i)$, 以每秒$(vx_i, vy_i, vz_i)$的速度移动(连续而非离散), 你从$ 0 $号点出发前往$ 1 $号点, 每次可以从一颗星球跳到另一颗或等待, 过程中不能在一颗星球连续停留$ s $秒, 求最大跳跃距离最小值.
$ n\le 1000 $
显然二分答案, 问题变成给你一张图每个边有一个出现时间, 不能连续停留$ s $, 问是否连通. 而对于某时刻有边的连通块, 你总可以不断在一条边左右横条刷时间相当于没有$ s $的限制.
那么直接扫当前时间, 维护当前所有点的度数, 维护$ v_i $表示点$ i $是否可达, 每次可能会加入一条边时bfs更新$ v $, 删除一条边时如果一边变成孤立点就记录时间, 如果某个点变成孤立点超过$ s $更新$ v_i $.
发现$ v_i $的总变化次数是$ O(n)$的(一开始全false,$ n $次删边可能把true变成false). 于是总复杂度是$(n+m)\log n $的.
B. 博弈问题
给定有根树, 点有权值$ w_i $, 定义一颗子树的权值是A先选一个点$ x $, B再选一个与$ x $不同的点$ y $, 得到的值$ v=w_x\mathrm{xor}w_y $, 且A希望最大化B希望最小化, 最终得到的$ v $, 求所有子树的$ v $.
$ n\le 10^5 $
看到两个数异或直接上字典树, 设$ f_u $表示字典树上以$ u $为根的子树作为整棵树并从中选两个数最终的权值, 则若当前点有一边没儿子就直接$ f_u=f_v $($ v $是$ u $的某个儿子), 否则如果有一边子树内只有一个数$ x $, 则一定选择那一个数, 再从另一边子树中选和他异或起来最小的数记为$ y=calc(x, v)$,$ calc $是单log的, 所以一次更新当前点的操作是单log的, 用线段树的形式支持插入一个数/合并总复杂度就是2log的.
C. 兔子猜拳
有$ n $个$ n $维向量$ x_1\ldots x_n $, 初始$ x_i $只有第$ i $位为$ 1 $其他位置为$ 0 $, 每次任选两个向量$ u, v $(有序), 另$ u=2u-v $并删除$ v $, 进行$ n-1 $次, 求最后得到的向量可能有多少种.
$ n\le 500 $
是AGC022F Checkers加个$ 0 $.
就是进行$ n $次合并每次保留一个, 考虑把合并模型建成树, 若$ u, v $合并保留$ u $则$ v $向$ u $连边最终形成根向树, 把子树按照合并的先后顺序从左到右排序, 意义是先子树内合并, 再把得到的每个儿子从左到右依次和父亲合并每次都是删除儿子对应的向量. 而考虑第$ i $位最终的值, 则每次第$ i $维有值的点$ u $与另一个点$ v $合并时, 若保留$ u $则这一维乘$ -1 $, 保留$ v $则乘$ 2 $, 而发现在这棵树上, 保留$ v $的次数就是点的深度. 而保留$ u $的次数则是每一层左边的儿子的个数之和加上自己的儿子个数之和, 若设点$ y $的$ -1 $的次数为$ c_y $, 则$ c_y=(c_{fa_y}-s_{fa_y})+(l_y+s_y)$, 其中$ s_u $表示$ u $的儿子个数,$ l_u $表示自己左边点的个数(以后都只在模$ 2 $意义下讨论$ c, s, l $).
考虑怎么进行dp, 两种情况最后相同要求所有点对应深度相同且符号相同. 层数到底是多少无关紧要, 设$ f_i $表示$ i $点最后一层有$ j $个点, 每次枚举$ x, y $表示新的一层中最后$ c_y $为$ 0/1 $的点的个数, 那么方案数就是选出这一层的点并分配奇偶.
但是这不对: 加入下一层的时候会导致这一层的一些点$ u $的$ s_u $变成$ 1 $使得$ c_u $变化, 并且本层儿子个数为奇数的点(简称奇点/偶点)的个数和下一层的$ x, y $相关. 若本层只有偶点必然要求$ x=y $(下一层点$ fa $相同的点的$ s_u $都是$ 0 $,$ s_{fa_u}-l_u $为$ 01 $交替,$ c_{fa_u} $相同, 所以最后$ 01 $个数相同的), 而若奇点中有两个点$ a, b $满足$ c_a\ne c_b $, 则交换$ a, b $会获得等价的, 奇点数减$ 2 $的状态所以可以要求奇数点的$ c $全都相同(等于$ x, y $中个数大的那一个对应颜色).
于是设有$ k $个点下一层子树大小为奇数, 状态为$ f_{i, j, k, 0/1} $, 其中最后一个$ 01 $是这$ k $个点的$ c $值. 于是下一层的$ x+y=j, \vert x-y\vert=k, [x>y]=0/1 $, (下面以$ x>y $为例), 枚举$ k’$, 转移系数就是组合数选出最后实际上为$ 0/1 $的$ x-k, y+k $个点:$ \binom{n-i}{x\mp k’, y\pm k’} $.
这样做复杂度是单$ n^4 $($ n^3 $状态加枚举$ k’$), 发现$ j $是没必要的状态(就是$ x+y $, 且不需做区分), 另外让$ k $带符号表示$ x-y $去掉01一维.
喵的不会, 这是官方的$ n^3 $

不是很懂两种做法本质区别导致一种可以优化一种不会.
NOI2024省选模拟赛24
A. 划分串
给定整数$ M, K $, 对于一个01串$ S $, 如果存在一个切分, 使得$ S(1, i)$与$ S(i+1, n)$的最大公共前缀长度大于等于$ K $, 那么称是$ S $的精准切分. 如果$ S $至少有$ M $个精准切分, 那么称$ S $是一个切分串. 给定$ N $, 问有多少长度为$ N $的切分串.
$ n\le 1000 $
简单题, 显然就是前$ k $位出现超过$ m $次, 枚举前$ k $位设为$ t $, 设$ f_{i, j, l} $表示前$ i $位,$ t $出现了$ j $次, 匹配了$ t $的前$ l $位, 暴力转移复杂度为$ nmk2^k $. 运算量有$ 10^9 $
看起来不太能过, 我的改进是让$ j $只枚举到$ \dfrac{i}{x} $, 其中$ x $为$ t $的最短循环节长度, 运算量大概$ 10^7 $
然而还有更厉害的, 打表发现输出范围内, 对同一个$ k $, 可以把$ 2^k $分成不超过$ 10 $种等价类, 每种的答案相同.
B. 降落伞环
有一张图初始全是散点,$ q $次询问, 每次加一条边, 获得问对当前的图, 有多少点满足删除这个点后剩下的所有连通块都是链(不包括环).
$ n\le 10^6, q\le 10^6 $
考虑链有两个条件: 不是环, 度数小于$ 3 $. 而如果有节点度数大于等于$ 3 $, 那么可能的答案不超过$ 4 $(它自己和它相连的最多$ 3 $个点, 如果它相连的点更多则那些点都不能成为答案).
于是把问题分成所有点度数小于$ 2 $和有点度数大于$ 2 $两部分, 第一部分再分成没环和有环两部分, 没环时输出$ n $, 有一个环时输出$ 1 $, 有两个环时因为度数小于$ 2 $所以环不交答案为$ 0 $. 第二部分只要对$ O(1)$个固定点check, 于是一开始直接不加有关他们的所有边, 判断剩下的点有没有环和三度的即可.
用vector建图被卡爆了, 这种每个点度数很小但总边数挺大的用vector会很慢.
C. 螺旋
给定$ a_n $,$ q $次询问对于给定的区间$[l, r]$, 最长的满足$ a_{l’}=a_{r’}, \forall i\in [l’, r’] a_i\le a_{l’} $的子区间$[l’, r’]$长度.
$ n, q\le 5\times 10^5 $
赛时先想了一个$ n\sqrt n $, 考虑根号分治, 对于次数大于根号的可以$ O(n)$直接扫一遍出答案, 对次数小于根号的颜色$ c $考虑枚举有序对$(x, y)$满足$ a_x=a_y=c $, 这样的有序对有$ n\sqrt n $个, 每个可以看成一个2side矩形赋值为max, 而查询单点查, 只要支持$ O(1)$前缀取max和$ O(\sqrt n)$单点查, 发现是简单的(对前缀$ p $取max改为把值插入到位置$ p $)
然后赛时又想了一个poly log, 考虑因为有$ l’, r’$区间不会相交, 所以可以类似建树的处理, 对于区间$[l, r]$要求$ a_l=a_r=x $为该区间的最大值(非严格, 该区间可能有其他最大值, 一个包含$ cnt $个$ x $的区间对应的点相当于上面做法$ cnt^2 $个可能的答案),$ x $把它分成若干子区间, 点$(l, r, x)$向每个子区间连边, 容易发现一共有$ O(n)$个$(l, r, x)$的对, 那么我们查找一个询问$ L, R $的时候, 一定是找到最浅的点$(l, r, x)$, 使得$ L, R $包含至少两个在$[l, r]$中的$ x $(不一定是$ a_l $和$ a_r $), 则该询问的答案可能有这个点贡献, 设$[l, r]$中被$[L, R]$包含的最左最右的$ x $分别为$ p_1, p_2 $, 则答案还有可能出现在$[L, p_1], [p_2, R]$, 发现对于$[L, p_1]$中的区间$(l’, r’, x’)$, 其一定贡献一个后缀($[k, r’]$), 同理对于$[p_2, R]$的一定贡献一个前缀, 于是这样的只有$ O(n)$个可能贡献的位置了. 于是解法就有了: 对每个$[L, R]$找到对应最浅$(l, r, x)$是简单的, 后面计算$ O(n)$个可能区间的贡献也是简单的, 总复杂度$(n+q)\log n $.
更厉害的出现了:  , 很巧妙的把全局和部分的联系在了一起.
, 很巧妙的把全局和部分的联系在了一起.
更厉害的出现了: std$ n\sqrt {n\log n} $跑$ 5\times 10^5 $
NOI2024省选模拟赛25
A. Lost Kingdom
给定$ n $点$ m $条边连通无向图, 可以选任意多个连通块, 对连通块的点集和边集分别求交最大化连通块个数.
$ n\le 10^5 $
在他给了样例解释之后变得毫无难度: “选$ 4 $个边集:$ U- $环上一条边”
于是注意到用$ U-{e} $这个边集$ E $可以在最后交的图中删去$ e $这条边, 条件是$ E $连通也就是$ e $不是割边. 而对于割边如果连通块不包含它必然要把它的一边扔了, 一定不优, 所以答案就是保留所有割边的连通块数.
B. Lighthouse
原题Gym103446C
有$ n\times m $的矩阵, 每个位置可能为$ 0 $,$ 1 $, 一次于$(i, j)$的操作可以覆盖同行同列且与$(i, j)$之间没有$ 1 $的所有$ 0 $, 现在又有一些位置是$ 2 $可以任意变成$ 1 $或$ 0 $, 求所有情况下要让所有$ 0 $覆盖至少一次的最小操作次数.
$ n\times m\le 190 $
这个题一开始数据范围给$ n, m\le 190 $让人很不会.
容易想到$ n\times m\le 190\Rightarrow \max(n, m)\le 13 $, 设$ n>m $.
于是直接轮廓线dp逐行做, 设状态要记录轮廓线上每个点 已经被覆盖且能提供向下面的覆盖, 被覆盖, 未被覆盖即需要向上的覆盖$ 3 $种情况, 同时一个点还可能被同行横向覆盖, 也要记录进去, 设$ f_{i, j, S, 0/1/2} $表示dp到第$ i, j $这个格子,$ S $为轮廓线上格子覆盖的$ 3^m $种情况,$ 0/1/2 $表示这一行前面的格子 已经有提供横向覆盖的/已经有要求横向覆盖的/没有要求没有提供 的情况.
状态数和复杂度是$ 3nm3^m $, 写出来开O2跑12s.
考虑优化, 极端情况当然是$ n=14, m=13 $, 所有位置全是$ 2 $之类的($ 2 $的格子要做两种转移), 考虑直接写个不优的东西乱跑一个解当最优性剪枝.
C. Dark Blue
原题Gym102803E
给定一个字符串的后缀数组sa和height数组$ h $的一部分(用$ -1 $代表未知), 求字典序最小的满足条件的小写字母构成的字符串$ s $.
$ n\le 10^6 $
设$ suf_i=s_{i\ldots n} $
感觉绕到后缀树上反而远了, 直接在字符串上, 对于$ i $, 有$ suf_{sa_i}<suf_{sa_{i+1}} $, 对于$ h $给定的情况, 就是$ \forall i, \forall j\in[0, h_i), s_{sa_{i-1}+j}=s_{sa_i+j}, s_{sa_{i-1}+h_i}<s_{sa_i+h_i} $, 那么可以用并查集把相等的元素合并起来, 小于关系只有$ O(n)$可以随便做了.
对于有$ h_i=-1 $的情况, 考虑要满足$ suf_{sa_{i-1}}<suf_{sa_i} $,$ suf_{sa_{i-1}+1} $和$ suf_{sa_i+1} $, 如果前者小则$ s_{sa_{i-1}}\le s_{sa_i} $, 否则$ s_{sa_{i-1}}<s_{sa_i} $.
并查集合并可以用 ds里P3295 [SCOI2016]萌萌哒的做法做到$ n\log n\alpha(n)$, 然后小于和小于等于统一成小于变成差分, 得到一张图, 字典序最小对应最长路, 然后scc必须是$ 0 $权边全相等, 求完scc然后乱做了.
NOI2024省选模拟赛26
计数专题-程思元
Gym102538H. Horrible Cycles
二分图, 每个左侧点和右边一个前缀$ 1\ldots a_i $连边, 求简单环数量.
$ n\le 5000 $
把$ a $从小到大排序, 每次加入一个左侧点和若干个右侧点, 显然只考虑一部分点一个环表现为若干条链, 设考虑左边前$ i $个点, 组成$ j $条链的环数为$ f_{i, j} $, 则每次可以新增一个链/合并两个链/什么也不做, 最后合并到只剩一个链的方案数为$ f_{n, 1} $, 要去除单点/单边/交换一条链的两个端点的贡献.
AT_hitachi2020_f Preserve Diameter
给定$ n $点树$ G $, 要求再添加若干条边形成简单图$ H $, 满足$ H, G $直径相同且再添加任意一条边$ H $直径变小. 求$ H $方案数
$ n\le 2\times 10^5 $
$ H $最后只有一个直径, 不然可以把其他直径两端连起来.
只有一个直径后, 以一个端点$ s $当做根建bfs树, 显然要求同层点和相邻层点边全连, 其他不连, 也就是每个点的深度唯一确定这张图. 而可行的深度序列$ dep $要求$ dep_s=0, \exist t, dep_t=d, \forall u\ne t, dep_u<d, \forall (u, v)\in G, \vert dep_u-dep_v\vert\le 1 $, 没了.
那么按照树上子树结构dp, 因为$ G $的直径可能很多考虑按照$ G $直径中点$ x $为根, 要求,$ dep_y-dep_x=\pm\dfrac{d}{2} $的恰好各一个, 设$ f_{u, 0/1/2, 0/1/2} $表示$ u $的子树,$ dep_y-dep_x $的值分别为$ 0/1/\ge 2 $个的方案数即可. 复杂度线性.
CF1450H2 Multithreading
考虑相邻同色点直接连不劣, 连完之后是$ \text{wb} $重复$ k $次的序列交替形式, 此时异色边相交数为$ \dfrac{k}{2} $, 问题变为求$ k $,发现$ k $是偶数下标与奇数下标上$ \text{w} $的个数之差(一次匹配删一奇一偶).
设奇数, 偶数上分别有$ a $,$ b $个$ \text{w} $,$ x $,$ y $个$ \text{? } $, 设$ x<y $, 枚举$ k $得到答案为
$$
\begin{gathered}
ans =\sum_i \sum_j \vert a-b+i-j\vert\binom{x}{i}\binom{y}{j}\
let a-b=c, i-j=d\
=\sum_d \vert c+d\vert\sum_i \binom{x}{i}\binom{y}{i+d}\
\because \sum_{i=0}^{\infty}\binom{x}{i}\binom{y}{i+d}=\sum_{i=0}^{\infty}\binom{x}{x-i}\binom{y}{i+d}=\binom{x+y}{x+d}\
\therefore
ans =\sum_d \vert c+d\vert\binom{x+y}{x+d}
\end{gathered}
$$
显然拆开绝对值, 现在要计算
$$
\begin{gathered}
\sum_{d=l, d\bmod 2=t}^r(c+d)\binom{x+y}{x+d}\
=(c-x)\sum_d\binom{x+y}{x+d}+\sum_d (x+d)\binom{x+y}{x+d}\
=(c-x)\sum_d \binom{x+y}{x+d}+(x+y)\sum_d \binom{x+y-1}{x+d-1}\
\because \sum_{d=t\bmod 2, d\bmod 2=t}^r\binom{n}{d}=\sum_{d=t\bmod 2, d\bmod 2=t}^r \binom{n-1}{d-1}+\binom{n-1}{d}=\sum_d^r \binom{n-1}{d}
\end{gathered}
$$
于是都变成了求组合数行前缀和, 可以快速维护.
在此之前让我们学习析合树
对一个排列, 定义一个连续段为区间满足重排后值也是连续区间, 非平凡连续段是除了单个元素和整个序列, 而一个本原段定义为一个连续段, 且不存在另一个连续段和它相交(可以包含), 发现任意连续段都可以分解成本原段的并.
本原段有包含关系可以建树, 建的时候区分子树且保留原序列顺序, 此时定义合点为儿子本原段的值域是升序/降序, 析点为其他点
上结论:
- 合点的区间中任意选一段都是连续段, 析点区间任意选非平凡的一段一定不是连续段.
- 析点儿子数量至少为$ 4 $.
- 合点儿子中合点必须和父亲反向(若父亲儿子序列递增则该儿子的儿子序列递减), 合点儿子数量至少为$ 2 $.
- 符合以上内容的都是合法的析合树.
试看看
CF1089I Interval-Free Permutations 或 LOJ3397「2020-2021 集训队作业」春天, 在积雪下结一成形, 抽枝发芽
求长$ n $没有非平凡连续段的排列数.
CF题$ n\le 400 $, loj3397$ n\le 100000 $
上析合树, 答案为析点为根且高度为$ 2 $的数量, 设其OGF为$ F $, 设根为合点且儿子递增的排列数的OGF为$ G $, 排列的OGF为$ H+1 $($ H $无常数), 则根为析点的析合树GF为$ H-(2G-x)$(对于长$ 1 $的序列正反相同减去). 同时根为析点的排列数量为$ F(H)-x $了.
于是有方程
$$
\begin{gathered}
G=\dfrac{(H-G)^2}{1-(H-G)}\
F(H)=H-(2G-x)
\end{gathered}
$$
于是有设$ H(R)=x $, 第一个式子变形成$ G(x)=\dfrac{H^2}{1+H} $则代入得$ G(R)=\dfrac{x^2}{1+x} $, 第二个式子得到$ F=x-2G(R)-R=x-2\dfrac{x^2}{1+x}-R $, 现在只要求$ R $. 这个和 count 中P4566 [CTSC2018] 青蕈领主完全一样.
P7278 纯洁憧憬
求长$ n $且至少存在一个长度大于$ k $的非平凡连续段的排列.
$ k\le n\le 400 $
先容斥成求没有大于$ k $的.
析合树, 对析点要求所有儿子大不超过$ k $, 对合点要求第一个, 最后一个儿子分别大于等于$ n-k $且小于等于$ k $
设满足限制的析点, 合点个数为$ F $,$ G $, 满足不存在非平凡连续段的方案数为$ H $, 全排列为$ P $,$ A=\dfrac{1}{1-F-G} $, 则$ F=H(P^{\le k}), g_n=\sum_{i\ge n-k}\sum_{j\ge n-k} (f_i+g_i)(f_j+g_j)(a_{n-i-j})$, 是不是这么跑暴力就$ n^3 $了啊.
然后std是再dp一步, 对于合点有限制的儿子都是边上, 所以可以设$ p_n $为长$ n $任何前缀不是非平凡连续段的排列个数, 则$ p_n=n! -\sum_{i=1}^{n-1} p_i (n-i)! $(容斥类的转移), 则$ g_n=\sum_i \sum_j p_ip_j(n-i-j)! $对于析点也是求出$ H $暴力复合.
NOI2024省选模拟赛27
A. 不休陀螺
有$ n $张牌组成一个序列, 每张牌用一个二元组$(a_i, b_i)$表示, 意味着打出这张牌需要消耗$ a_i $点费用, 打出后可以获得$ b_i $点费用. 接下来你可以选择一个区间$ l, r $将这个区间中的卡取出来作为你的卡组.
开始时你的卡组会按照随机顺序排列并且你有$ E $点费用, 然后你会依次从前往后打出这个排列中的卡. 当你打完这个排列中的卡后你的卡组又会重新随机排列然后你再依次打出, 直到你无法再打出下一张牌(当前费用小于下一张牌需要消耗的费用)时停止. 如果一个卡组无论在什么情况下都能够无限打下去, 我们则称这卡组可以”陀螺无限”. 现在求有多少个区间组成的卡组能够”陀螺无限”.
$ n\le 10^6 $
简单题, 对于区间$[l, r]$, 合法的条件是区间和大于$ 0 $且$ E+sum_{<0}\ge \max_{a_i> b_i} a_i \sum_{a_i>b_i} $,$ E+sum_{<0}> a_i-(b_i-a_i)$, 其中$ sum_{<0} $为所有$ b_i-a_i<0 $的和, 于是对每个右端点找到满足后两个条件的最小左端点, 然后前缀和二维数点.
B. 染色
在$ 2^n\times 2^n $的$ 01 $矩阵上, 每次可以选定位置让上下左右相邻位置及其本身共$ 5 $个位置取反, 认为第一列和最后一列相邻, 第一行和最后一行相邻.
构造从全$ 0 $矩阵弄出指定状态方案.
$ n\le 11 $
只会暴力高消, 设前两行的推别的, 可以发现方程数和位置数相等, 所以应该都有解. 又考虑到弄出$ 1 $就行了, 然而不会弄$ 1 $于是寄了.
考虑要弄一个$ 1 $, 一个可行的构造是对于一个当前全$ 0 $局面, 假设要构造$(0, 0)$位置是$ 1 $, 操作$(0, 0)$会出现上下左右多余的$ 4 $个$ 1 $, 分别操作这$ 4 $个位置会变成多余$(0, 2), (2, 0), (0, -2), (-2, 0)$四个$ 1 $, 记集合$ S_i={(0, 2^i), (2^i, 0), (0, -2^i), (-2^i, 0)} $, 发现用得到$ S_i $的操作去操作$ S $中的每个点会得到$ S_{i+1} $, 而当$ i=n $的时候$ S $重合没了, 于是就弄出一个$ 1 $.
逐层模拟以上过程即可.
更厉害的做法, 题目等价于给定$ F(x, y)$, 计算$ F(x, y)(1+x+x^{-1}+y+y^{-1})^{-1}\bmod (x^{2^n}-1) \bmod (y^{2^n}-1) \bmod 2 $(设操作为$ A(x, y)$, 其中$[x^iy^j]A\in [0, 1]$表示是否操作$ i, j $, 则卷上$ 1+x+x^{-1}+y+y^{-1} $再模一下是结果, 所以要求逆. )
然后有对质数$ p $有$ f^p(x)\equiv f(x^p)\pmod p $, 这个是考虑对于多项式系数$ \binom{p}{a_1\ldots a_k}=\dfrac{p! }{a_1! \ldots a_k! }, (p=\sum a_i)$要想没有$ p $因子只能是$ a_i=p $.
有$(1+x+x^{-1}+y+y^{-1})^{2^n}=1 $, 于是要求$ F(x, y)(1+x+x^{-1}+y+y^{-1})^{2n-1} $.
C. 计算
设$ F(x, a, b)=\gcd(x^a-1, x^b-1)+1, x>0 $, 特殊规定$ F(x, 0, b)=F(x, a, 0)=0 $, 给定$ m, a, b, c, d $, 设$ L=F(m, a, b)+1, R=F(m, c, d)$求$[L, R]$有多少子集是$ m $的倍数.
$ m\le 10^7, a, b, c, d\le 3000, L, R\le 10^{18} $
首先把$ L, R $求了, 设$ a<b $, 考虑要算$ \gcd(x^a-1, x^b-1)=(x-1)\gcd(\sum_{i=0}^a x^i, \sum_{i=0}^b x^i)$,$ \gcd(\sum_{i=0}^a x^i, \sum_{i=0}^b x^i)=\gcd(\sum_{i=0}^a x^i, \sum_{i=a+1}^b x^i)=\gcd(\sum_{i=0}^a x^i, x^{a+1}\sum_{i=0}^{b-a-1} x^i)=\gcd(\sum_{i=0}^a x^i, \sum_{i=0}^{b-a-1} x^i)$, 于是可以用类似$ gcd $的递归简单算这个. 特殊的记住有$ F(x, a, b)=x^k $的性质.
那么接下来算子集和, 设$ F=\prod_{i=L}^R (1+x^i)=\prod_{i=0}^{m-1}(1+x)^{iC} $(所有东西出现次数相同, 由刚才$ R-L+1=x^{k_1}-x^{k_2} $得到), 容易想到单位根反演, 于是答案写成
$$
\begin{gathered}
ans=\sum_{i}[m\vert i][x^i]F(x)=\dfrac{1}{m}\sum_i\sum_{j=0}^{m-1}w_m^{ij}[x^i]F(x)=\dfrac{1}{m}\sum_{j=0}^{m-1}F(w_m^j)\
F(w_m^j)=\prod_i (1+w_m^{ij})^{C}\
\because w_m^{ij\bmod m}=w_m^{ij}
\therefore\ let\ d=\gcd(m, j)\
F(w_m^j)=\prod_{i=0}^{m/d}(1+w_{m/d}^j)^{dC}\
\because \prod_{i=0}^m (x-w_m^i)=x^m-1\
\therefore
F(w_m^j)=((-1)^{m/d}\prod_{i=0}^{m/d}(-1-w_{m/d}^j))^{dC}=2^{dC}[2\vert \dfrac{m}{d}]\
\let\ f_d=2^{dC}[2\vert \dfrac{m}{d}]
\therefore ans=\dfrac{1}{m}\sum_{i=1}^{m}f_{\gcd(i, m)}=\dfrac{1}{m}\sum_{d \vert m}f_d\sum_{i}^{m/d}[i\perp \dfrac{m}{d}]=\dfrac{1}{m}\sum_{d\vert m}f_d\varphi(\dfrac{m}{d})
\end{gathered}
$$
赛时被这个$ \prod_{i=0}^m (1+w_{m}^{ij})^C $整不会了/kk
D. 鸡
对于一个非负整数序列$ a $, 定义它对应的独立集序列$ f(a)$: 假设将$ a_i $改为$ 0 $, 此时选出若干个两两不相邻的数使得它们的和最大, 则$ f(a)_i $. 表示和的最大值. 现在给定$ n, m $, 求有多少个长度为$ n $的非负整数序列$ b $满足存在至少一个长度为$ n $, 值域为$[0, m]$的非负整数序列$ a $使得$ f(a)=b $. 答案对给定的质数$ MOD $取模.
$ n, m\le 300 $
设$ B $为$ b $的全局最大值, 也就是$ a $的全局最大独立集, 设$ c_i=B-b_i $, 则容易发现相邻两个$ c_i $至少有一个为$ 0 $, 把$ c_i $分为$ 0 $和$>0 $两类,$ c_i>0 $是全局独立集的元素而$ c_i=0 $的可能是. 当$ c $确定了$ b $的相对大小就确定了, 于是考虑对于每个$ c $, 另其权值为$ B $的取值范围大小, 则累加所有$ c $的权值即为答案.
容易发现对于一个$ c $,$ B $的最小值就是$ \sum c_i $, 而最大值分开考虑.
对于$ c_i=0 $的极长连续段, 这一段在$ b $中的值相等, 发现如果左端点左边存在$ c_i\ne 0 $, 那么左端点一定不会进入独立集, 否则会对外面造成影响同时中间不变, 右端点同理, 于是可以删掉左右端点, 设中间剩下长度为$ x $, 可填入$ \lfloor\dfrac{x}{2}\rfloor $个数奇数则留空一个, 数大小任取贡献即$ \lfloor\dfrac{x}{2}\rfloor m $
对于$ c_i>0 $的每个数单独考虑, 一定是独立集中元素, 且不小于$ c_i $, 上界看起来是$ m $, 但存在情况不是: 对于序列$ c=p0x0x0x0x0q $其中$ p, q>x $或$ p0, 0q $不存在顶到序列边界, 设从第一个$ x $到最后一个$ x $的区间长$ l $, 因为删去第一个$ x $的最优解一定包含$ p $(根据$ p>x $)同理有删去最后一个$ x $一定包含$ q $, 于是删去它后区间外方案不变,$ p, q $之间显然最大是$(l-1)m+x $($ l-1 $个位置填$ m $剩下一个填$ x $), 就行了.
于是可以拆贡献, 一个$ c $序列的贡献是所有极长$ 0 $段加上所有$ c_i\ne 0 $减去$ p0x0x0q $的贡献, 分别计算, 设$ f_i $表示一个长$ i $的段, 每个位置属于$[0, m]$没有选到两个连续的$ 0 $(即$ c $序列方案数),$ g $表示$ f\times f $, 就能算了.
NOI2024省选模拟赛28
A. 树的重心
给定一棵树求有多少个连通块的重心与这棵树相同.
$ n\le 5000 $
显然容易$ n^2 $求出以$ u $子树与$ u $连通的部分大小为$ x $的方案数, 设为$ f_{u, x} $, 则如果有两个重心吸纳然要求两个一条边的两个子树大小相同, 直接做复杂度就是对的. 对于只有一个重心的要求没有一棵子树大于一半, 先不管限制卷起来再容斥掉大于一半的即可, 复杂度也是$ n^2 $.
B. 匹配
给定一个$ 2n $个点$ m $条边的二分图, 左部点编号为$ 1\sim n $右部点编号为$ n+1\sim 2n $. 给定每条边为黑色或白色, 你需要找到一个完美匹配, 使得匹配里的黑色边数恰好为偶数.
$ \sum n\le 500 $
容易想到先随便找一个匹配调整, 则接下来要找一个有奇数条黑边的环, 容易想到把每个点拆两个最短路, 或者随机一个点为根找所有返祖边形成的环也能过.
C. deadline
给定二分图, 左边有$ n $个点, 右边有$ m $个点, 有$ k $条边, 右边点有黑/白色, 左边点颜色任选, 求只保留同色边的情况下最大匹配的最小值.
$ n, m\le 2000, k\le 5000 $
考虑网络流, 考虑最小割, 容易想到左边每个点拆两个$ u, u’$, 连边$ s \stackrel{inf}{\rightarrow} u, u’\stackrel{inf}{\rightarrow} t, u\stackrel{inf^2}{\rightarrow} u’$来使得每个点恰好选一边, 对每个右边的点, 若为白色连$ s\stackrel{inf^2}{\rightarrow} v $, 若为黑色连$ v\stackrel{inf^2}{t} $, 对一条边$ x\to y $, 若$ y $为白色连$ x\to y $否则连$ y\to x’$边权为$ 1 $, 跑最大流即可.
最小割的好处是, 先割了一部分后剩下的仍然是一个最小割问题使得我们可以把二分图匹配问题嵌入进去.
D. 新本格魔法少女
todo
NOI2024省选模拟赛29
A. Easy
给定一个$ n $个点,$ m $条边的无向联通图第$ 0 $天未尾你在结点$ 1 $, 并且战斗力为$ l_1 $除了结点$ 1 $之外的$ n-1 $个节点都有BOSS, 第$ I $节点BOSS的战斗力可以表示为$ l_i $. 每天你可以挑战最多一个BOSS, 到其所在结点打败他, 前提是当前结点到BOSS结点的一条路径上没有其他BOSS存活.
当你的战斗力大于该BOSS时, BOSS会被消灭, 否则不能挑战该BOSS. 当击败一名BOSS, 奖励的经验值会使你的战斗力提高$ A $. 而每天的一开始, BOSS的战斗力会提高$ B $.
你必须打败结点n的BOSS来获得游戏的胜利. 问是否存在这样的方案, 如果存在, 最少需要多少天?
$ n, m, A, B, l_i\le 21\times 10^5 $
容易想到当$ A-B<0 $时就是直接写dij(第一次到达一定最优), 当$ A-B>0 $时任何一个曾经能到的节点将来都能到所以维护当前能到的所有节点, 不断拓展, 当能到节点数不大于当前天数就说明无解, 当当前能到的节点包含$ n $时胜利.
B. 幂
对所有$ x\in [1, A], y\in [1, B]$求有多少种不同的$ x^y $
容易想到把$[1, A]$中$ a $相同的$ a^b $拿出来一起处理, 则$ b>1 $的就只有根号了, 考虑计算答案比$ AB $少多少(算重了多少).
则钦定每个数$ a^c $被最小的$ b\vert c $的$ a^b $表示, 于是$ a^x $会表示的数就是$ c(x)=\sum_{S\subset {1\ldots x-1}} c(S)(-1)^{\vert S\vert} $, 其中$ c(S)$表示能同时被$ S $中所有数表示的数的个数, 容易发现其为$ \dfrac{m\cdot g_S}{\mathrm{lca(S)}} $, 其中$ g_S $表示$ S $中最小元素, 直接做复杂度是$ 2^29 $过不了, 但是注意到如果新加入元素已经被$ lca(S)$表示则加/不加的所有方案构成双射贡献为$ 0 $, 就过了.
C. 哈夫曼回路
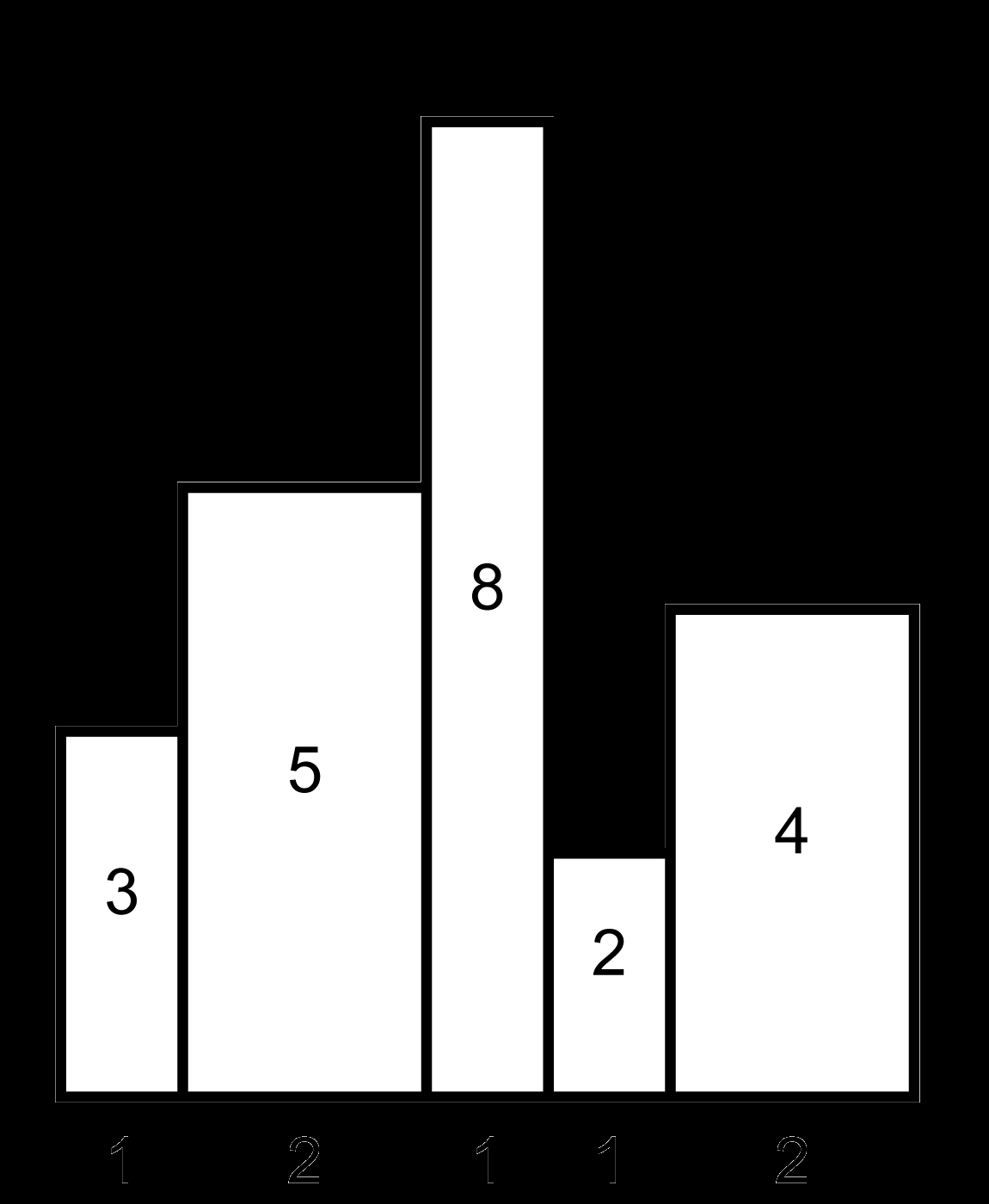

$ n, q\le 10^5, w_i, h_i\le 10^6 $
考虑任意两个匹配都不在边上相交否则直接交换即可, 于是容易发现匹配只会在同一个矩形中, 于是直接线段树结构分治做即可.
D. 模拟赛
$ A\times B $网格上有$ n $个点, 求矩形对数使得每个点至少被一个矩形覆盖
$ n, A, B\le 10^5 $
这种题和上一次碰到的历史研究类似, 都先考虑所有点横竖方向最大的点带来的性质. 现在设所有点的上, 下, 左, 右界分别为$ U, D, L, R $构成矩形$ R_0 $. 考虑现在确定第一个矩形$ R_1 $为$ u, d, l, r $, 分类考虑第二个矩形的范围. 下面包含均指严格包含(非边界覆盖)
分类之后扫描线即可. 附上官方题解, 但其实不用线段树, 直接二分就能做的.
NOI2024省选模拟赛30
A. Y
你有一个随机生成器, 每次会均匀随机地生成一个$[0, m]$之间的整数. 你用这个随机生成器生成了$ 2n $个整数, 你想知道你生成的前$ n $个整数的和比后$ n $个整数的和大的概率是多少. 你只需求出这个概率对质数$ P $取模后的结果即可.
$ T, n, m\le 1000 $
前两天是不是刚做了一个谁比谁大相当于赢得和输的双射, 只要求平局数量的题.
[trick] 输赢双射后求平局数量
于是直接GF, 把后$ n $个数每个数求相反数相当于提取$ 0 $项
$$
\begin{gathered}
[x^0]\left(\dfrac{1-x^{m+1}}{1-x}\right)^n\left(\dfrac{1-x^{-m-1}}{1-x^{-1}}\right)^n\
=[x^m]\left(\dfrac{(x^{m+1}-1)^2}{(x-1)^2}\right)^n
=[x^m]\left(\dfrac{x^{m+1}-1}{x-1}\right)^{2n}
\end{gathered}
$$
而分子和分母逆的展开式都是简单的, 于是直接线性卷就做完了.
B. hashit
初始为空的字符串$ S $,$ q $次操作, 每次末尾增删字符, 每次操作后询问本质不同子串数.
$ q\le 10^5 $
容易想到离线后操作树, 想到字典树, 建广义SAM, 一个操作的答案对应操作树上到根的链构成的字符串的本质不同子串, 对应字典树上到根链的本质不同子串, 对应sam上若干个节点到根的链的答案之和, 也就是要求到根的链并的权值和, 于是直接做就行了.
C. 点点的圈圈
给定$ n $个圆的圆心$(x_i, y_i)$和半径$ r_i $, 保证没有相交和相切, 第$ i $个圆价值为$ w_i $要求选出最多的互不相交的圆.
$ n\le 10^5 $
首先容易发现如果建出树就是简单题, 乱dp即可.
于是只要给每个点找父亲, 这种题没有相交就是在说上下关系不变让你扫描线, 但是圆不好扫, 分成上半圆和下半圆去做即可, 注意扫描线可能不能容易的找到父亲, 此时找到一个兄弟也能知道父亲.
D. 图上的游戏
交互题,$ n $点$ m $边图, 每次可以给定点集问是否连通, 要求问出图.$ n, m\le 600 $, 次数$ 3\times 10^4 $
考虑对于一条链已知点集和边集怎么做, 维护加入前若干点后这些点的顺序和两点之间的边集, 每次先二分出新点应该插入在哪两个点之间再逐个判断边应该加在哪边, 后面这不期望1log所以要先打乱.
考虑先求图的一棵生成树, 从$ 1 $到$ n $加点, 维护若干条链加点的时候可以而分出这个点在哪条链或者不在任何已有的链上, 不在任何已有的链上时可以对边集二分出这条链的边. 经过这一步之后可以得到每个链的边集和点集, 在dfs序上二分可以得到每个链的父亲节点, 然后用链的方法处理.
对于图剩下的边考虑从叶子到根处理, 在dfs序上二分出每个边的另一端是谁, 然后剥掉叶子重复, 就做完了.
NOI2024省选模拟赛31
A. X
JOI准高速列车的背景

$ k\le 2500, x\le 2500, S_{i+1}-S_i=10000 $
显然每段是独立的, 对于单独一段, 考虑dp怎么划分子问题, 发现一个两端点都修建站台的区间是子问题, 此外要知道两个端点各还能走多远, 于是设$ f_{i, a, b} $表示长$ i $的区间左边还能走$ a $步右边还能走$ b $步的方案数就做完了.
B. 装饰
有$ 2\times m $的矩阵, 要求用$ 3 $种颜色涂色, 满足第$ i $种颜色的数量恰好为$ c_i $, 相邻格子颜色不同, 任意$ 2\times 2 $区域包含所有种类的颜色. 求方案数.
$ m\le 10^6 $
考虑把上下两个作为一个整体考虑, 若当前位置填$(1, 2)$下一个只能填$(2, 3)$或$(3, 1)$, 而$(2, 3)$下一个只能填$(3, 1)$或$(1, 2)$,$(3, 1)$下面只能填$(1, 2)$和$(2, 3)$, 即上下两个看起来有$ 6 $种可能, 但一种填色方案只出现$ 3 $种, 问题变成了给定$ c_1, c_2, c_3 $, 要求没有两个颜色相邻的方案数.
后面这个问题直接插板组合数即可, 枚举第二个颜色插到第一个颜色中时还有相邻两个都是第一个颜色的位置.
C. 和谐宇宙

$ n\le 6\times 10^5, tp\le 2 $
对树的这种连通块计数.$ E $的权值可以变成逆元做, 相当于问所有方案的连通块的边权积之和.$ tp=1 $是直接dp, 对于$ tp=2 $考虑两个连通块要么有祖孙关系要么没有, 有的部分在每个节点$ u $, 统计$ u $子树内连通块和包含$ fa_u $的连通块之间的贡献. 没有祖先关系的在每个$ u $统计不同子树之间的贡献. 换根要维护孩子前后缀背包(背包以满足选至少三个分支)
为什么不能直接待删背包? 因为这里只会维护$ g_{u, 1/2/3} $表示选$ 1, 2, \ge 3 $个分支的情况, 而删除权值为$ w $的物品时$ g_{u, 3} $要除掉$ \dfrac{1}{w+1} $, 题目只保证$ w $有逆元而不保证$ w+1 $有就寄了. 只能前后缀背包合并.
D. 黑鸭的序列
对$ \forall i\in [1, V]$建树$ G $使得$ fa_i=\lfloor \sqrt i\rfloor $, 设树高为$ H $, 设数$ i $高为$ dep_i $. 则显然我们要求区间内的数的$ lca $的深度$ d $, 答案即为$(r-l+1)d-\sum_i dep_{a_i} $. 而要求lca可以考虑求dfs序最小/最大的lca, 但是dfs序不会求, 考虑这棵树的bfs序就是数的大小顺序, 而同一层的点dfs序的大小关系和bfs序相同, 于是把每层最小最大的数拿出来暴力lca即可.
于是显然要维护区间内深度和, 区间内每个深度中点的最大/最小值. 区间赋值直接打标记, 区间加考虑如果没有数的深度变化就打标记, 否则递归到左右儿子再合并信息.
定义势能$ \Phi=H-\sum_{u\in T} c_u $, 其中$ u $为线段树节点,$ c_u $为每个$ u $节点中存在的值$ v $的$ H-h_v $之和, 显然考虑区间赋值和初始情况总势能是$(n+q)\log n $的. 每次区间加的时候如果当前节点存在某个位置深度增加则暴力递归到两边后合并, 于是单次复杂度是$ \Delta \Phi\log n\log \log V $. 可以把$ \log \log V $去掉, 改为只上传发生变化的层的信息, 由于势能变化一只能变两层所以就是$ \Delta \Phi \log n $了.
然后一种常数优化是把递归改为标记下传时做而不是修改时做
NOI2024省选模拟赛32
A. Giao 徽的烤鸭
给定一棵树, 选点$ i $要付出代价$ w_i $, 若一个点距离$ p $以内的点都被选了收益$ v_p $, 最大化收益减代价.
$ n\le 2000 $
距离的限制是简单满足的, 只要直接dp,$ f_{i, j} $表示点$ i $距离$ j $以内的点都被选了, 转移的时候到父亲到儿子限制至少为$ i-1 $即可. 复杂度$ n^2 $
B. apers
给定有向图$ G $, 可以化$ c_u $代价选中点$ u $, 要求每条$ s\to t $路径上必须经过至少$ k $个选中的点.
$ n\le 200, m\le 500, k\le 5 $
$ k=1 $显然是最小割, 而且数据范围也很网络流, 考虑最小割拓展, 想到拆分层图.
于是建$ k $层$ G $,$ G $中每个点拆成$ u\stackrel{c_i}{\longrightarrow} u’$,
C. 字符串
给定字符串$ a_n, b_m $, 求有多少有序对$(i, j)$满足$ a_{1\ldots i}+a_{j\ldots n} $是$ b $的子串
$ n, m\le 5\times 10^5 $
相当于对$ b $每个本质不同子串数划分方式. 则设$ p_i $表示$ a_{i\ldots n} $与$ a $的lcp,$ q_i $表示$ a_{1\ldots i} $与$ a $的最长公共后缀, 显然区间$[l, r]$的划分数是$ \max(\min(l+p_l, r)-\max(r-q_r, l), 0)$.
sam的等价类要求每次对$ r $固定,$ l $位于一个区间的子串统计答案, 可以差分成对$ r $固定$ l $位于一个前缀, 扫描线, 然后看起来三个maxmin很难做但一拆发现三种情况都很好做, 只剩下$(l+p_l)-(r-q_r)$的情况, 要求$ l+p_l\in [r-q_r, r], r-q_r\ge l, l\le L $, 发现最也只有两维数点. 复杂度单log.
NOI2024省选模拟赛33
A. 塔
有长$ l $的数轴, 要求选编号为$ 1\ldots n $的$ n $个点, 对第$ i $个点要求距离其$<i $的位置没有选点. 模$ m $
$ n\le 100, m, l\le 10^9 $
$ l $很大, 考虑如果确定了点的排列$ p $, 则$ i, i+1 $两个点的距离要不小于$ b_i=\max p_i, p_{i+1} $, 设$ s=\sum b_i $, 那么对于确定的排列$ p $安排点的位置的方案数就是$ \binom{l-s+n-1}{n} $.
于是考虑计数$ s $为某固定值的排列数量, 排列计数且贡献只和相邻元素有关容易想到扫值域dp, 设$ f_{i, s, j, k} $表示当前插入最大的$ i $个数, 这些数的贡献为$ s $(每个数插入时贡献), 有$ j $个连续段, 且有$ k $个端点被占用, 转移即可, 复杂度$ n^4 $.
然后要求若干组合数, 因为$ n $很小可以矩阵快速幂, 复杂度$ n^3\log n $
B. 运输
$ n $点树,$ q $询问子树和, 链和, 或给定$ x, y, a $, 对每个$ u\in subtree(x)$加上$ dis(u, y)\cdot a $
$ n, q\le 2\times 10^5 $
容易想到按照$ y $是否在$ x $子树分类, 而$ y $在子树外的情况很简单, 相当于子树加$ dep\cdot v $和子树加.
对$ y $在子树内的情况, 子树询问ban掉了点分树, 考虑硬拆$ dep_u+dep_y-2dep_{lca(u, y)} $, 要给$ y $到$ x $这条链第一个点加$ -2dep\cdot a $, 后面链上每个点的子树加$ 2a $, 加的标记都记录在这条链上, 则一个点的值是自己记录的值加上祖先链的和, 剩下都很简单了.
C. 麻将
考虑dp of dp, 对于判定问题, 显然对麻将扫值域, 设$ f_{i, 0/1/2, 0/1/2, 0/1/2} $, 表示考虑前$ i $大的数, 当前有没有将,$ i-1 $的值的个数和$ i-2, i-1 $都有的值的个数.
对于数数问题, 看起来是设$ f_{i, j, S} $表示扫了前$ i $大的值选了$ j $个数当前内层dp状态为$ S $的方案数,$ S $很大过不了, 但是发现有用的$ S $个数很少($ 100 $个), 于是复杂度变成$ MKS $.
NOI2024省选模拟赛34
A. duyi 的切题树
交互题,有一棵高为$n$的完全二叉树,节点编号未知,求根的编号,每次可以问每个点的所有邻居的编号.你可以问$q$次.
$n\le 12,q\le 50$
容易想到对于一个点直接可以问出一条到叶子的链,可以先随便一个点问出三条链得到其深度.
然后假设现在在点$u$,深度为$h$,假设已知另外两条链长度为$h,l$(一定有一条是深度),那么可以直接跳到第二条链的第$(l-h)/2$个点,不断重复.然后其实这两条只要随便问出一条,如果长$h$就跳$u$不是这条链的那个邻居,否则跳$(l-h)/2$.这样询问次数是$\sum_{i=1}^12 i=78$.
容易发现最后$k$步直接爆搜要用$2^k-1$次,于是平衡出最优是$1+2\ldots +8+2^4-1=51$
最后爆搜$2^k-2$个点还没搜出来,直接排除,于是就$50$次.
是CF750F New Year and Finding Roots加强版
B. 红蓝大作战
给定$(2n)\times m$的01矩阵,其中$0,1$各$nm$个,给$0,1$各自两两连边构成向量($(a,b)$连向$(c,d)$得到向量$(c-a,d-b)$),要求把边定向后所有向量和为$0$.构造方案.
$nm\le 3000$
$nm$为奇数很简单,直接就是欧拉回路定向,因为向量绕一圈和为$0$.
对$nm$为偶数,要发现一个结论,保证颜色不同的两个对角点$a,b$各自连向同色点可以让这些边向量和为$0$.证明考虑对称的两个点,如果颜色不同显然是$0$,如果颜色相同则是由$a\to b$或$b\to a$的向量.因为$0,1$个数相等,两个方向的一样多所以最后是$0$.最后还是欧拉回路.
欧拉回路直接跑好像会爆,但完全无向图构造若干个环实在是很简单.(模几)
C. 发讲义
给定一棵$n$点树,两个人从根开始走,不能走向父亲,一个人可以在任意节点处传送到另一个人的位置,要求所有点都必须走到,求最短时间
$n\le 5\times 10^6$
上来第一个想法是一定是两个人一起往下走,走到第一个有分叉的地方之后先清理其它分叉,再留下最深的一个分叉,然后两人再同时往下走,把一个人传过来,这是错的,一个hack:根引出两条链,链靠近根处挂几个叶子,此时应该让一个人先去叶子,再传送回根,然后两个人同时走两条链.错误原因是可能先修剪掉浅处一些分叉使得最后剩下的两个分叉延伸更长.
因为两个人是不区分的,考虑一定可以看成两个人中的一个人没有传送过而另一个人不断传送到它,于是这个人走了一条到叶子的主链,会在若干关键点处停留,此时另一个人去清理到下一个关键点之间链外的叶子,当只剩一个最深的叶子时两人一起向下走.
于是可以dp,$f_u$表示$u$作为主链上的关键点时从根到$u$的部分耗费的时间,转移枚举祖先$v$作为上一个关键点,设$u$深度,子树叶子个数,子树叶子深度和,子树内且主链外最深的叶子深度分别为$d_u,c_u,s_u,m_u$,则转移为$f_u=f_v+(s_v-s_u)-d_v(c_v-c_u)+\max(0,(d_u-d_v)-\max_k m_k)$,可以上复杂数据结构斜率优化.
一个分叉不作为关键点一定是祖先上有一个延伸很长的叶子,至少要比自己长,于是点$u$一定会从$m_v\ge d_u$的地方转移过来.同时发现$m_v$更长且当前点更靠下的一定更优(单调),而且长过$u$的对$u$来说都一样,最后每个点只会从最近的$m_v\ge d_u$转移过来即可.
于是直接可撤销化单调栈$n\log n$即可.考虑普通单调栈,push一个点$m_u$时会 pop 掉$O(Height)$个点,于是先进短儿子再进长儿子,复杂度是线性的.
原是【UR #7】水题走四方