比赛记录
比赛记录
已经不光是比赛了, 还有看的成套的题.
已经又都是比赛了, 成套的题移走了.
ZSContest
很久以前写下zscontest的编号. . . zs是什么啊?
是不是振声啊
A [博弈论] [打表]
$n\times m$ 的网格上有若干硬币, 初始时全部为反, $q$ 次翻转一个矩形并询问, 若两人轮流操作, 每次先选择一枚正面硬币 $(x, y)$ , 再选择一个 $(a, y), a<x$ 或 $(x, b), b<y$ , 同时翻转这两个格子的硬币, 不能操作的人输, 是先手必胜还是后手必胜.
$n, m\le 10^9, q\le 10^5$
首先结论: 每一枚硬币是独立的. 这个操作实际上相当于硬币可以向左或向下移动若干步, 两枚硬币碰到一起就一起消失, 那么考虑假设硬币不会消失的情况和这个是等价的, 因为若选择移动多枚硬币位置相同, 后手仍然以相同方式移动这个位置到先手移动到的位置是不会让局面更优也不会更劣等, 所以是等价的.
于是每一枚硬币分别的SG值求出来异或, 打表SG值和其矩形前缀和找规律吧.
B
有 $n$ 个数对 $(a, b)$ 构成的集合, 给定 $m$ , $k$ 和集合, 求最小的 $t$ 满足有至少 $k$ 个不同子集的 $\sum a+bt\ge m$ .
$n, k\le 10^5, a, b, m\le 10^9$
二分答案是容易想到的, 于是变成了求有多少个子集和大于 $m$ 或子集和的第 $k$ 大.
一般rank总是比kth容易, 发现k并不到 $2^n-1$ , 我们的复杂度一定是相关 $k$ 的, 然后就不会了.
一个我没见过的经典题求所有子集合的第 $k$ 大, 解法是爆搜子集, 当前结果大于等于 $m$ 就返回, 否则把个数加一继续搜.
这个复杂度的分析是重点, qyc一开始说因为每次递归让方案数变大1, 最多到 $k$ (不然直接停), 于是就解决了, 但实际上, 若初始状态为全部不选, 连续若干个不选并不会增加方案数, 正确的做法是先递增排序, 这样如果前面的不选后面的更选不了可以直接跳, 就仍然有每次递归方案数变大1了.
然而这个题还有负数, 考虑我们搜大于等于 $m$ 的子集, 就要满足:
一旦和低于 $m$ 就能退出
若这个不选以后的也不能选
所以初始状态为选所有正数不选所有负数, 并按绝对值排序, 这样做保证如果当前这一位相比初始状态不能改变以后的也不行可以直接跳.
C [直径]
单点修改边权, 查子树直径. $n\le 10^5$ .
合并直径是简单的, 四个端点两两比一比就好了, 因为要查距离并支持修改所以用BIT维护点到根距离, 并用建在欧拉序上的线段树维护直径解决问题.
另一种做法是静态toptree说能1log, 但我还不会静态toptree, 需要学习一下.
D [FFT] [多项式]
给一个 $V\le 2$ 个点, 识别括号和空格的自动机, 字符集为 $(, ), space$ , 求有多少种从点 $s$ 到点 $t$ 走 $n$ 的方案行成合法括号串.
$n\le 10^5$
万恶多项式, 打完 $n\le 1000$ 走人.
等学了分治FFT再来.
22. 10. 10 VP CF1198 Codeforces Round #576 (Div. 1)
和wjw, 难度感觉不大到Div1.
过程大概是先切A, 然后看一眼B直接SegmentTreeBeats没冲出来发现自己不会STB. 然后去开C, D, E, F, 发现E好像可做. 仔细一想是个套路网络流把它冲出来了, 然后去做B写了个更简单的O(n)做法. 比赛结束.
wjw切了 $B\to A\to D$
A MP3
智障题.
B. Welfare State
单点改, 区间取max. $n, q\le 2\times 10^5$
写吉老师线段树的都降智.
直接离线, 对每个点考虑, 一个点的值是它最后一次修改的值和从这一次修改开始往后这一段时间取max的最大值. 复杂度线性.
所以CF这种短时间比赛反而更不能急着码, 多想想是不是可以写的简单点.
C. Matching vs Independent Set
给一个 $3n$ 个点, $m$ 条边的图, 你给出一个 $n$ 个点的独立集或一个 $n$ 个边的匹配.
$n\le 10^5, m\le 5\times 10^5$ . 多组询问.
qyc的做法, 任意求一棵dfs树, 如果叶子多于 $n$ 个就选叶子, 否则现在叶子少于 $n$ 个, 除了叶子每个点都可以和自己的父亲/儿子匹配, 于是至少有 $n$ 个边. 就结束了.
wjw看了看slime的做法, 说的是直接贪心求匹配(任意加边), 如果够 $n$ 条直接结束, 否则因为只使用了少于 $2n$ 个点, 且剩下的点已经选不出相邻的两个点形成匹配, 所以剩下的一起当独立集即可.
D. Rectangle Painting 1
给一个 $n\times n$ 的网格图, 一开始格子有黑有白, 每次你可以花费 $\max w, h$ 的代价将一个 $w\times h$ 的矩形染白, 求全白的最小代价.
$n\le 50$
降智题
做法是, 要么一个操作染了全局, 否则必然有一个未染色的分界点(分界成左上和右下), 然后可以递归下去做. 这样复杂度 $n^5$ .
还是不太敢想这种 $n^5$ 复杂度的东西啊, 明明是可以很简单的.
E. Rectangle Painting2
给一个 $n\times n$ 的网格图, 一开始格子有黑有白, 每次可以花费 $\min w, h$ 的代价将一个 $w\times h$ 的矩形染白, 求全白的最小代价.
黑色格子的给出方式是输入 $m$ 个矩形, 黑色格子为这 $m$ 个矩形的并.
$n\le 10^9, m\le 50$ .
套路题. 首先我们显然会每次将染一行或一列全染白, 于是就成了选若干行和列覆盖所有位置. 这个模型有点像网络流, 然后发现一个最小割结束战斗(行点列点, 行向列连 $inf$ , 起点, 终点向行列连1). 然后突然发现黑色格子是由矩形给出的. 不过没关系, 直接离散化, $m$ 个矩形在平面上切割的连通块数是 $m^2$ 的, 所以就是 $4m$ 个点, $m^2+2m$ 个边冲就好了.
F. GCD Groups 2
给出 $n$ 个整数, 要将它们划分成两个集合使得这两个集合各自 $\gcd$ 为1, 求方案或判断无解.
$n\le 10^5$
有点意思.
智慧法: 从前往后扫, 考虑第一个集合, 如果当前这个数不是 $\gcd$ 的倍数就加入这个一集合, 这样 $gcd$ 一定变小. 然后一遍肯定不对就randomshuffle. 正确的原因是, $10^9$ 的不同质因数个数只有9, $10^9$ 到质数大约有 $5\times 10^7$ 个很多, 所以很难出现一种状况让一整个集合有一个共同质因子.
官方正解(搬运翻译):
首先, 你只要用 $9$ 个数干掉每一个因子. 所以有解情况下必然由一种情况使得在其中一个集合大小不超过9.
然后随机取两个数钦定它们在不同的集合中, 这样同一个集合的概率很小(因为其中一个集合只有9个数). 然后对一个集合做状压dp(压掉当前还活着哪些质因子). 这样做复杂度是 $n\times 2^{2k}$ .
最后实际不需要全部 $n$ 个数做这个dp, 可以对每个素数取 $2k$ 个, 这个数量可以杀掉其他所有素数, 无论如何会有一个空余的可用. 复杂度 $k^2\times 2^{2k}$ .
官方正解真阴, 随机化万岁! .
22. 10. 12 VP CF1736 Codeforces Round #825 (Div. 2)
又是降智的一天呢!
A. Make A Equal to B
智障题
B. Playing with GCD
没切Div2B, 输麻从此刻开始
给定序列 $a_n$ , 判断是否有可能构造序列 $b_{n+1}$ 满足 $a_i=\gcd(b_i, b_{i+1})$ .
$\sum n\le 10^5$
把每一个数看作向量, $\gcd$ 是对向量每个元素取 $\min$ , 考虑如果你的向量 $b_i$ 的一个元素同时比 $a_i$ 和 $a_{i-1}$ 的对应元素大, 那么一定是不优的(你不能用它做取 $\min$ 了). 所以结论是 $b_i=\mathrm{lcm}{a_i, a_{i-1}}$ , 然后有可能不行, 所以再 check 一遍.
C1. Good Subarrays (Easy Version)
写麻烦做法, 继续寄
给定序列 $a_n$ , 求有多少子区间 $[l, r]$ 满足 $\forall i\in [l, r], \ a_i\ge {i-l+1}$
$\sum n\le 2\times 10^5$ , 多组询问
赛时写了个, 从后面往前扫, 每次给当前后缀区间减1, 二分第一个小于 $0$ 的位置. 总结应该是, 还是太着急写代码, 明明想到某些单调性但觉得这个不难写就直接冲了.
考虑每个位置减去下标, 问题变成 $\forall i\in [l, r]\ , a_i\ge -l+1$ .
然后考虑每个左端点, 合法的右端点是一个前缀, 并且每个左端点对应的合法右端点是单增的, 那么可以直接从上一个左端点的右端点开始往后扫就能处理出每个位置为左端点对应的右端点, 把这个数组记为 $r$ .
不过看起来不给前后缀区间减一没有关系, 重点是要发现右端点单增可以直接扫
C2. Good Subarrays (Hard Version)
接着刚才的做法, 区别是加了独立的单点询问.
发现改小是直接二维数点(平面上线段, 求矩形内线的总长), 改大比较问号, 我们根本不会追溯修改.
然后我在错误的道路上越走越远了.
然后汪娟突然跳出来: 改大不是比改小简单吗?
是的! 我们是智障! , 因为改大的时候, 你只会改一个数, 所以对一个 $i$ , 可以处理若 $r_i+1$ 被改对了那么新的 $r_i$ 是几, 就做完了.
CF官方题解上改大和改小是同一个处理厉害了
Public NOIP Round #3 (Div. 1, 提高)
A. 移除石子
给定平面上 $n$ 个点, 构造选择 $\dfrac{n}{2}$ 个正方形的方案使得每个正方形内恰好有两个点, 且正方形覆盖了所有点.
$T\le 60, n\le 3000, x_i, y_i\le 10^9$
每个点对建一个点, 然后从构成点对的两个点指向代表点对的点, 遍历每个点对, 如果这个点对 $u$ 组成的矩形上或内有另一个点 $v$ 则连边 $u\to v$ , 然后在图上跑拓扑排序.
不对, 边数 $n^3$ , 一个矩形内可能有一摞点.
考虑从左往右扫, 如果当前左边的点没法消, 就把它插入到操作序列的最后, 否则放在操作序列的最前面, 就可以了.
提高不会A是怎么回事啊
然后qyc说, 汪娟看了这场说只会D, 于是看D
D. 数圈圈
给定一个 $n\times m$ 网格, 每个位置是一个小写字母, 求有多少个矩形满足边框上字母相同.
$n, m\le 2000$
直接对每个位置预处理向右向下向左向上最远到哪里, 那么枚举一个左上角, 就要求一个矩形内所有向左向上超过左上角坐标位置的, 就直接数点了. 要对每个颜色分开做即可.
诶不对, 这是2log的, 死了.
考虑竖着分治, 画一条横线, 考虑穿过它的矩形, 那么现在我们可以用 $n^2$ 的时间去干一层.
我们预处理每个位置向上向下延伸多远, 然后确定左边的一条竖线, 向右扫描, 维护当前有多少个向右的横线, 在每个竖线统计答案.
对于维护横线这一步, 我们先预处理出所有向右的横线, 然后在一个位置加入贡献, 在另一个位置删除贡献即可.
A, C todo
CSP-S 2022
遗憾疫情把csp杀了
T1 假期计划(holiday)
给定 $Graph(n, m)$ , 点有点权 $w_i$ , 求 $a, b, c, d$ 满足 $1\to a\to b\to c\to d\to 1$ 这条路径中两两点距离不超过 $k$ , 且最大化 $w_a+w_b+w_c+w_d$ .
$n\le 2500, m\le 10000, k\le 100$
先 $nm$ 求一遍距离应该没什么异议.
考虑 $n^2$ , 而且只出 $a, b, c, d$ 肯定是让你枚举的, 一般这种都是中间的比较重要, 考虑枚举 $b, c$ , 于是现在要确定 $a, c$ , 直接对每个点 $u$ 处理 $1\to u$ 路途中点权的最大的, 次大的, 发现还是可能重复, 那就再处理次次大的, 发现肯定行了.
问号 $k\le 100$ 是干什么的?
T2 策略游戏(game)
给定 $a_n, b_m$ , $q$ 次询问, 每次给定参数 $l_1, r_1, l_2, r_2$ , 求A先从 $a_{ [l_1, r_1] }$ 中选一个数, B再从 $b_{ [l_2, r_2] }$ 中选一个数, A想最大化两数乘积, B想最小化, 求最后乘积是多少.
$n, m, q\le 10^5$
那就是最小值的最大值, 分正负数讨论, 然后用随便什么RMQ做就了.
T3 星战(galaxy)
给定有向图 $Graph(n, m)$ , $q$ 次操作, 每次删去一个边, 或恢复一条之前被删掉的边, 或删掉连向一个点的所有入边, 或恢复一个点的所有入边, 或者问当前的图是不是所有点出度为 $1$ .
$n, m, q\le 5\times 10^5$
光想着对度数搞根号分治了
考虑hash边集, 维护全局hash值, 那么处理每个点周围的hash, 操作点直接做, 操作边要改全局hash和连向的点的hash即可.
为什么脑子里总是没有随机化这根弦啊?
T4 数据传输 (transmit)
给定 $Tree(n)$ , 点有点权 $w_i$ , $q$ 次询问对于点 $u, v$ , 选定序列 $c$ , 使得序列相邻两项距离不超过 $k$ , 序列首/末项到 $u$ / $v$ 的距离不超过 $k$ , 序列中点的权值和的最小值.
$n, q\le 2\times 10^5, k\le 3$
$k\le 3$ ! ! !
直接DDP $f_{u, 0/1/2}$ 表示上一个点距离自己 $0/1/2$ 的情况的最小权值, 这里正反是一样的, 所以从 $u, v$ 分别矩阵乘到lca, 然后在lca处合并.
但是当 $k=3$ 的时候, 有可能选择一个不在 $u, v$ 路径上的点, 但发现那样的话必然是路径上的点的儿子, 所以动态dp的时候搞一下权值就行了.
UPD: 写了代码, 这个题不难写, 注意一下那个不在路径上的点要算上父亲.
ZSContest 20221105
C0A 分开了哦算
给定括号序列 $s_n$ 和括号的颜色 $c_n\in {0, 1, 2}$ , 每次可一1代价翻转一个括号, 颜色不能改变, 求最小代价使得 $c_i\in {0, 2}$ 和 $c_i\in {1, 2}$ 的括号分别组成合法括号串.
$n\le 5000$
考虑一个经典结论, 在插入/修改一个括号序列使其合法的时候, 只把一个前缀的右括号改成左括号, 一个后缀的右括号改成左括号是不劣的. 证明可以考虑括号序列把(看作 $+1$ , )看作 $-1$ 的一个折现, 每次修改一个括号是给一个后缀加/减2, 最后要所有位置都不低于0且最后位置等于0, 那就显然了.
于是一个 $n^3$ 做法是枚举 $c_i=2$ 的括号被修改的前后缀, 在确定了它之后确定另外两个就是简单的了(就是给定一个括号串, 其中若干位置不能改, 要求改成一个合法的, 只要从前往后扫, 每次如果前缀和小于0就把一个最靠前的左括号改成右括号, 最后不断把最靠右的右括号改成左括号, 可以开俩堆).
考虑不枚举前后缀, 转而枚举 $c_i=0$ 的括号的和, 这样一来另外两种括号的和同样是确定的, 那么先通过操作最左, 最右的括号把它的和调整对, 在这个基础上, 求出不断把最左边右括号变成左, 最右左括号变成右, 直到不能变了的情况下每个位置被弄到的次数, 设为 $x, y, z$ , 模拟一遍就出每个位置当前的值, 设当前位置堆三个颜色的操作次数为 $x’, y’, z’$ , 于是对每个位置就有了一个限制, 就是 $\min(x, x’)+\min(z, z’)>C$ , $C$ 是确定的常数, 于是把min拆开, 就成了关于 $x’, y’, z’$ 的线性规划, 合并限制后限制数量很少所以可以直接手枚顶点.
最后发现当枚举的 $c_i=0$ 的括号的和从大到小的时候, 可以维护 $x, y, z$ 每次最多变化1, 线段树合并限制, 复杂度1log.
C0B 自身的成功
给定 $n\times m$ 的01矩阵, 每次可以把一个0变成1, 同一行同一列的1变成0, 给定两个局面问是否可以把第一个变成第二个.
$n, m\le 1000$
如果有一个0变成1, 并且这个1的同行同列有1, 那一定死了, 于是现在没有这种情况.
如果所有的都是1变成0, 最后全是0, 也死了.
考虑先把所有0变成1的点了, 一定不劣, 然后现在要清除所有1变成0, 那就找到一个可以操作的行/列(最后没有1), 然后用这行/列干掉这个1即可. 如果找不到就死了.
C0C 阿克最最易
ZR题
C0D 最成功捧杯
给定 $n\times m$ 矩阵, 你在奇数步可以横着任意走, 偶数步可以竖着任意走, 每个位置有颜色 $a_{i, j}$ , 求走 $k$ 步形成的颜色序列个数.
$n, m\le 10, k\le 600, a_{i, j}\in [1, 9]$
考虑dpofdp, 那么考虑给定一个颜色序列如何dp判断可行, 可以 $f_{i}=S$ 表示前 $i$ 位走完可能走到的点是集合 $S$ . 但这个内层状态过大: 可能有一种颜色出现次数很大, 所以考虑做到 $n, m$ 相关: 每一次对于一行/一列, 有多个颜色和有一个是一样的, 只要记录 $f_{i}=S$ 表示前 $i$ 个走完之后可以走的行/列的集合是 $S$ 即可, 此时内层状态数是 $k(2^n+2^m)$ .
然后考虑dpofdp, 扫掉一维 $i$ 后外层dp的状态是内层的值 $S$ , 于是 $f_{i, S, j}$ 表示颜色序列前 $i$ 个, 走到的集合是 $S$ , 最后一个位置颜色是 $j$ 即可, 预处理转移, dp复杂度是 $(2^n+2^m)k\Sigma$ .
ZSContest 20221116 on Vjudge
赛时会3个, T4没longlong半天没查出来
abc259h
给定 $n\times n$ 矩形, 每个位置有值 $a_i$ , 只能往下或往右走, 问有多少起点终点值相同的格路径.
$n\le 400$
这里用 $n$ 表示题目中的 $n^2$
考虑两个很显然的暴力:
- 枚举颜色 $c$ , $f_{i, j}$ 表示以颜色 $c$ 开头走到 $i, j$ 的方案数dp.
- 枚举颜色 $c$ , 枚举 $c$ 中的两个位置, 以这两个位置为起点, 终点的路径是一个简单组合数.
于是根号分治, 出现次数大于 $\sqrt n$ 的用第一种, 出现次数小于 $\sqrt n$ 的用第二种. 第一部分复杂度显然 $n\sqrt n$ , 第二部分是
$$
\begin{gathered}
\max \sum {a_i}^2\
s. t.
\sum a_i=n
\ a_i\le \sqrt n
\end{gathered}
$$
这个式子量级是经典的 $n \sqrt n$
[think] 经典复杂度分析! 在做完SDOI2022D1T1后你又差点忘了.
abc264h
给定 $T=Tree(n)$ , 对每个 $k$ 求只保留编号不超过 $k$ 的点的情况下 $T$ 有多少个导出子图是满二叉树(每个点有两个儿子, 所有叶子深度相同). 保证父亲编号小于儿子.
$n\le 3\times 10^5$
重点是, 因为是满二叉树, 所以二叉树深度只有 $\log n$ 量级.
于是直接dp, $f_{i, j}$ 表示点 $i$ 的子树内选深度 $j$ 的二叉树, 那么转移是简单的. 然后因为保证父亲编号小于儿子所以就算不断挂叶子, 因为只有深度在 $\log n$ 以内的节点可能对根的dp值有贡献所以每次暴力往上跳更新就是对的.
abc255g
$n$ 堆石子的nim游戏, 有 $m$ 个限制, 第 $i$ 个限制 $x_i, y_i$ 表示若一个石子堆剩余石子为 $x_i$ , 你就不能从其中拿走 $y_i$ 个. 问先手必胜/必负.
$n, m\le 2\times 10^5, a_i\le 10^{18}$
公平组合游戏, 只需要考虑求一个石子堆的 SG 值, 最后异或起来判断即可.
没有限制的时候显然是 $SG(x)=x$ , 那么加上限制之后会有若干个特殊点和若干段 $y=x+k$ 的一次函数. 没有限制的点的值显然是前面的最大值加1, 而有限制的点可以考虑维护每个 $SG(x)$ 的出现次数, 不断删掉被禁止的 $x$ , 找到最小的删没了的 $SG(x)$ 就是当前的SG值.
但是直接维护 $SG(x)$ 会爆炸, 但发现只维护特殊点的就行, 其他的位置的次数就是一个默认的 $1$ .
abc264g
有 $n$ 个字符串, 每个字符串 $t_i$ 长度不超过 $3$ 且有权值 $p_i$ , 一个字符串 $s$ 的总权值为 $\sum_{i=1}^n cnt(s, t_i)\times p_i$ , 其中 $cnt(a, b)$ 表示 $b$ 在 $a$ 中出现的次数. 问长度任意的 $s$ 的权值是多少, 若可以无穷大输出 $\texttt{Infinity}$ .
$n\le 18278, \vert w_i\vert \le 10^9$
第一感觉是很离谱, 尤其是长度不限, 并且不会处理各个 $t$ 之间拼接之后包含的新的 $t$ .
这个长度3很特点, 发现如果长度2可以直接每个字母建一个点, 然后弄一下边权, 那么现在考虑直接建点 $(a, b)$ 表示当前字母是 $b$ , 上一个字母是 $a$ , 权值就又可以用点之间的边表示了.
注意起点终点和长度为1, 2的字符串的细节.
NOIP模拟赛Day1
A. string
给定 $S_n, T_m$, $q$ 次询问对于 $k$, 最小的 $p$ 满足 $p\cdot S$ 不是 $k\cdot T$ 的子序列. 乘法是重复若干次.
$n, m\le 5000, k\le 10^14, q\le 3\times 10^5$
处理从 $S$ 每个位置开始跑一个 $T$ 会匹配几个, 到哪.
然后再拼接这个, 显然最多 $n$ 次出循环, 找到循环次数并处理这 $n$ 次的答案即可 $O(1)$ 回答询问.
B. path
给定 $Tree(n)$, $q$ 次询问对于 $x, y$ 有多少个路径恰好以 $x\to y$ 的链为交集. 膜 $998244353$.
$n, q\le 3\times 10^5$
等等, 这不是那个离谱lyh多项式题吗? K Path, 哦, 这是那个题 $k=2$ 的弱化.
那就考虑 $x, y$ 分成祖孙链和其他, 设 $f_u, g_u$ 表示从 $u$ 向子树内/外引两条链不交的方案数. 这个随便平方啥的搞一搞就行了.
最后统计答案就是, 如果 $x$ 是 $y$ 的祖先答案是 $g_xf_y$, 否则是 $f_xf_y$.
C. triangle
给定 $Tree(n)$, 有边权, 对每个 $x$ 求所有有序对 $(x, y, z)$ 的 $dis(x, y)+dis(y, z)+dis(x, z)\pmod L$ 最小值.
$n\le 3000$
考虑三个点的虚树形成一个三叉, 那么显然一定要枚举一个三叉的中点.
注意到, 对于一个三叉, 至少有两个点在中点的子树里, 那么枚举这两个点, 就成了从两个集合各选一个数最大化它们的和膜 $L$. 这个只要直接二分即可. 如果外面有 $x$ 个点, 里面有 $y$ 个点, 复杂度就是 $(x+y)\log(x+y)$, 注意到 $\sum x$ 和 $\sum y$ 都是 $n^2$ 级别的.
另一个想法是直接枚举 $x$, 然后边分治.
D. draw

$n, q\le 3\times 10^5, a_i\le 4$
一个暴力显然是每次从能打的里面拿最大的. 另外断坏成链也是经典套路.
这种打牌抽牌的一个经典套路是做前缀和描述当前手牌数变化.
考虑先确定打出的 $1$ 的数量, 显然只有更大的打完了才会用 $1$, 所以此时可以看成 $2, 3, 4$ 的牌都是拿到立刻打, 打够 $p$ 次说明没有 $1$, 中间没有 $2, 3, 4$ 打了的时候才会用 $1$. 这个可以用一个前缀和实现: 把 $1$ 当成 $0$(拿了也不打), 对当前手牌数做前缀和就是对于 $2, 3, 4$, $a_i=a_{i-1}+1, 2, 3$, 否则 $a_i=a_{i-1}-1$. 那么因为这个数组是可差分的, 找到第一个 $a_i<a_s+k$ 的就说明要打 $1$ 了, 也可以类比着找到所有打 $1$ 的位置. 这么往上弄就好了. 对这个倍增优化一下复杂度就1log.
另一个问题是要确定当前是否有比自己小的能打, 这个只要直接对着所有数前缀和即可求出一个边界满足在这个边界内总有非0牌可以打.
KFC NOIP 2022(20221125wjw模拟赛)
A. move
给定 $2n\times 2n$ 的棋盘, 有 $n^2$ 个棋子在左上角 $n\times n$ 的地方, 要都移动到右下角 $n\times n$ 的地方, 每次可以把一行棋子左右移动/一列棋子上下移动, 棋盘上有若干不能放棋子的障碍, 障碍有权值, 求移除最少障碍使得可以移动过去.
$n\le 1000$
诈骗题(但被诈骗了), 只要考虑 $(1, 1), (1, n), (n, n), (n, 1)$ 四个位置的棋子要移过去要满足的条件是八个位置(固定的)中的一个没有障碍, 而其他棋子都可以通过这种方式移动走.
B. path
给定 $Graph(n, m)$, 边有边权, $q$ 次询问 $u\to v$ 路径上边权序列的前缀与形成的集合的 $\mathrm{mex}$.
$n, q\le 10^5, m\le 5\times 10^5$
首先因为前缀与, 答案不超过 $2$(包含 $1$ 一定不会包含 $2$), 于是思考判定.
答案是 $0$ 说明至少有一位全程都是 $1$, 那么对每位单独判保留这位是 $1$ 的边能不能连通, 并查集即可, 条件是至少一位的连通块连通.
再考虑判定 $1$, 那么如果没有 $1$, 考虑是路径上在到 $0$ 之前一定都要在非末位上有 $1$, 那就是 $u$ 和 $v$ 的连通块之间用一条末位是 $0$ 的边连接即可, 仍然并查集维护连通块标记一下即可. 又因为可以走到0只要出去随便绕一绕总是能到 $0$ 的.
C. sequence
给定 $a_n$, $q$ 次单点修改或者询问区间最小的 $a_i\mathrm{or} a_j, i\ne j$.
$n, q\le 10^5$
Source: CF1665E
结论题.
[trick] 值域小于 $2^k$ 的数中选两个数 $\mathrm{or}$ 起来最小值出现在前 $k+1$ 个里.
考虑归纳, 如果第 $k$ 位有 $2$ 个 $0$, 那么一定选 $0$, 剩下的是前 $k-1$ 情况下的最小值. 否则第 $k$ 位最后是 $1$, 只要最小化前 $k-1$ 位, 对应了前 $k-1$ 位的最小值和这一位是 $1$ 的数中的最小值.
于是直接线段树就是 $\log^2 n$
D. color
给定 $Tree(n)$, 点有颜色 $c_i$, 求 $\sum_i ((\sum_j s(i, j)) \mathrm{xor} i)$, 其中 $s(i, j)$ 表示从 $i$ 到 $j$ 的颜色数.
$n\le 10^6$
赛时做法
考虑一个换根(思路来自 P6556), 那么发现就是加上那些到这个点路径上没有当前颜色的点这样的贡献, 只要对每个颜色求虚树, 然后虚树dp即可, 另外就是可能会有求 $u$ 的一个是 $v$ 的祖先的儿子这样的会有 $\log n$.
常数写大了, 赛后在loj上看了下是能进1s的.
std
实际上不需要虚树, 考虑到当前这个点的路径上没有当前颜色的点形成的连通块只有 $O(n)$ 个, 所以直接求每个连通块大小即可. 可以线性.
点分治
被wjw对着卡了. 复杂度1log.
NOIP2022
输麻, 省队无缘
A. plant
给定 $n\times m$ 01矩阵, 求有多少个1组成的C形和F形.
$n, m\le 1000$
每个位置处理向下向右到哪, 然后简单前缀和/二阶前缀和统计.
多测清空
B. meow
给定 $n$ 个栈和序列 $a_m\in [1, k]$, 初始一个变量 $p=1$, 有两种操作: 1. 选择一个栈压入 $a_p$, 然后 $p\leftarrow p+1$, 如果栈顶两元素相等则同时消去. 2. 选择两个栈底元素相同的栈消去栈底.
k\le 2n-1, n\le 300, m\le 2\times 10^6
考虑 $k=2n-2$ 的情况是容易的, 容易想到 $n-1$ 个栈里每个栈存两种元素, 下一个元素如果是栈顶直接消, 栈底放到空栈消, 不存在则找一个元素个数小于 $2$ 的放进去.
$k=2n-1$ 时, 存在情况 $n-1$ 个栈大小为 $2$, 又出现一个新的元素 $a_x$ 不存在于任意一个栈里, 考虑现在有两种方案, 要么放到一个栈顶, 要么放入空栈.
我们希望局面始终保持在: 任意一个元素至多出现一次, 那么考虑如果 $a_{x+1}$ 存在于栈底, 只需要放到 $a_{x+1}$ 所在的栈顶然后把栈底消了. 而如果 $a_{x+1}$ 在栈顶则有可能被 $a_x$ 遮住, 并且可能接下来出现 $n-1$ 个元素使得不存在一个栈不会被遮住.
于是考虑下一个栈底元素 $a_y$, 而 $a_{x+1}\ldots a_{y-1}$ 全位于栈顶. 考虑处理 $a_x, a_y$ 之间元素后的局面: 如果 $a_y$ 所在栈的栈顶元素 $c$ 出现了奇数次, 那么恰好露出 $a_y$, 于是一开始 $a_x$ 进空栈即可. 如果 $c$ 出现偶数次, 那么把 $a_x$ 放到 $c$ 上面, 上面的 $c$ 正好全消了, 再让 $a_y$ 消去栈底即可.
问题解决.
C. barrack
给定 $Graph(n, m)$, 保证连通, 求有多少种方案选定一个点集, 再设立若干条关键边, 使得删去任意一条非关键边不会使点集不连通, 膜 $10^9+7$.
$n\le 5\times 10^5, m\le 10^6$
考虑直接边双, 接下来的问题是给定一棵树, 对每个虚树求有多少种边集可以连通它.
一个想法是设 $f_u$ 子树内选了点的边连通块与 $u$ 连通, 剩下的边任意的方案数, 问题是边连通块内点随便选时, 有一部分点都没选的情况会在边连通块更小, 但外面随便选的时候重复计算, 为了避免才钦定边连通块是选的点集的虚树.
那么统计虚树, 设 $f_u$ 表示 $u$ 子树内选, 且点的虚树根为 $u$ 的方案数, 则答案是每个 $u$ 处统计上 $f_u$ 乘 $u$ 子树外的边的随便选的和, 设 $g_{u, 0/1}$ 表示去掉虚树根的限制, 根选/不选, 转移显然, 最后容斥一下可得到 $f$. 复杂度线性.
D. match
给定 $a_n$, $b_n$, $q$ 次询问对于给定的 $[l, r]$, $\sum_{l’<r’\in [l, r]} \max_{i\in [l’, r’]} \max_{j\in [l’, r’]} a_ib_j$
$n, q\le 2. 5\times 10^5$
考虑扫描线, 对于给定的右端点 $r$, 设 $f_i$ 表示以 $i$ 开始的答案区间的答案, 那么询问就是求和, 每次右端点挪动的时候会给每个区间新加一个, 那么再维护两个区间对应最大值位置(从 $r$ 开始向前的前缀 $\max$), 就成了两个数组区间赋值, 以及区间加上他俩对应相乘, 可以线段树, 复杂度 $n\log n$.
需要维护的矩阵: 
230218qyc contest
A 秋天就要做偷橙子的梦
给定一个数列 $a_n$, 其中除了一个数之外每个都出现了 $k$ 次, 这个数小于 $k$ 次, 求这个数
空间限制1mb, $n\le 2\times 10^7, a_i\le 10^9$
有个广为人知题是所有数出现两次, 一个出现一次, 直接异或就做完了.
那么开始考虑k进制下不进位加, 发现只能扫两遍.
但实际上搞k进制不进位加是闲的, 直接二进制不进位加起来, 最后mod k就算完了.
现在复杂度瓶颈是对每一位分别求和, 实际上还可以优化到 $O(n)$ 而不是 $O(n\log v)$
考虑假设序列是静态的做法, 可以序列分治, 每次合并左右两边的 $\log v$ 个和, 此时合并可以做到 $\log n$, 方法是用 $\log n$ 个数, 其中第 $i$ 个数的第 $j$ 位表示第 $j$ 个和的第 $i$ 位是几, 合并的时候用加法器那一套就行了. 然后每次合并代价是 $\log len$, 所以总复杂度就线性.
此时变成动态的, 上一个二进制分组即可.
B 你喜欢OI南桐轻小说吗?
计算两个序列 $a, b$ 的LPCS Longest Pairing Common Subequence, 也即一个最长的长偶数的序列 $c$, 设它的长度是 $k$, 它要满足对于正整数 $i\leq \frac{k}{2}$ 有 $c_{2i-1}=c_{2i}$, 且它同时是 $a, b$ 的子序列. 输出长度.
$n, m\leq 5000, a_i, b_i\leq 10^4$.
空间限制 $8mb$
考虑一个朴素dp, $f_{i, j}$ 表示已经选了长 $i$ 的, 其中在 $a$ 中最后一个选的是 $a_j$ 的情况下, $b$ 数组中最后一个最早是谁.
前缀和优化转移显然, 问题在于转移需要 $O(1)$ 算 $nxt(j, a_i)$ 表示在 $i$ 之后第一个 $a_i$ 的位置, 直接存显然爆了.
于是常数比较小时间换空间冲了.
好吧实际上, 你用 $f_{i, j}$ 表示 $a$ 里选了 $i$ 个, $b$ 里选了 $j$ 个的方案数, 此时假设先扫第一维, 就只会从 $(last_a(i), j’)$ 转移来, 其中 $b_{j’}=a_i$, 所以复杂度是奇妙的线性.
C 关于摆烂地交通部长摆烂这档事
给定一张 $DAG(n, m)$, 求有多少个点满足它能到达和能到它的恰好是全部的点.
$n\le 5\times 10^5, m\le 10^6$
考虑把DAG从左往右摊开, 可以删掉跨过这个点的边(从这个点左边到右边), 那么发现在剩下的图中满足条件等价于左边的点出度不为0, 右边的点入度不为0.
于是要维护一个删边情况下每个点的出入度, 注意到按照拓扑序遍历点的时候每个边影响一个区间, 于是差分贡献就能做到线性.
230318qyc contest
F - Figglypuff Gym - 102341J
直接猜结论
但把一个简单代码写复杂了, 太久不写代码
E - Enteractive Vertex
首先这种东西肯定让你二分, 你一想可以用 $\log n$ 的代价得到特殊点在某个点的哪个子树里, 那么肯定上一个点分治, 目前可以卡到 $2\log n$
注意到, 如果卡成 $2\log n$ 一定是这个点有一堆特别小的子树, 那么按子树大小排序, 找到前 $k$ 小使得它们大小之和恰好大于一半, 先确定答案是不是在这一半里, 简单分析发现变成了单log
B - Brammarly Gym - 102331G
第一眼想建SAM, 多看几眼发现如果走重一定是一个相等的段, 变成了简单组合题.
D - Dypno Gym - 102341H
考虑可以用 $\dfrac{3}{2}$ 的代价硬通过一条边, 或者去试探.
那么对于一个点, 最优策略一定是从能到的点中, 最小的到更大的去试探一个前缀, 当试探后的收益小雨直接冲就不试了.
那么这个已经可以dp了, 用dij优化, 注意到对于两个点可以根据它们答案最小的后继的答案去比较(放到dij的堆里).
A - Aevee Gym - 102341E
考虑容斥, 计算有 $k$ 个不合法长 $l$ 段的方案数, 那么组合数就是每个栈第一个不合法的往上随便拿, 然后连着拿这 $l$ 个, 然后再随便拿. . . , 注意到若有两个都不合法, 则一定要满足这两个颜色在每个栈里都是一个在另一个上面, 于是你设 $f_i$ 表示以 $i$ 颜色结尾的LCIS的贡献(带容斥系数)去dp.
那么你枚举一个左端点, 开始往右扫右端点, 注意到每次往右延伸一个右端点时, 一个 $i$ 所能转移到的 $j$ 就会减半, 在一次向右扫的过程中, 每个 $i$ 只会转移线性次, 所以复杂度是 $nk\max(n, k)$ 这样的.
230513qyc contest
CF1696D
给出一个 $1$ 到 $n$ 的排列 $[a_1, a_2, \dots, a_n]$ . 对于 $1\le i < j\le n$ , 记 $\mathrm{mn}(i, j)$ 为 $\min\limits_{k=i}^j a_k$ , 记 $\mathrm{mx}(i, j)$ 为 $\max\limits_{k=i}^j a_k$ .
有一张 $n$ 个点的无向图, 点的编号为 $1$ 到 $n$ . 对于每一对整数 $1\le i<j\le n$ , 如果同时满足 $\mathrm{mn}(i, j)=a_i$ 且 $\mathrm{mx}(i, j)=a_j$ , 或同时满足 $\mathrm{mn}(i, j)=a_j$ 和 $\mathrm{mx}(i, j)=a_i$ , 那么就在 $i$ 和 $j$ 之间连一条长度为 $1$ 的边.
询问这张图中从 $1$ 到 $n$ 的最短路的长度. 可以证明 $1$ 和 $n$ 总是连通, 所以最短路总是存在.
$n\le 5\times 10^5$
考虑你不会往回走.
考虑对于最大值, 你至少需要一步跨过它, 最小值也是, 于是一种写法是你每次找到最大值最小值, 然后中间一定是从最小值走到最大值, 两边递归.
贪心的方式是, 直接找到能走到最长段.
Baekjoon - 23416
有两个刀片, 分别可以把蛋糕切成相等的 $a, b$ 份, 现在让你切两刀, 最小化最大块最小块极差. $a, b\le 100$
考虑如果两个刀片数量相等答案显然是 $0$.
那么设 $a<b$, 显然最大值是 $1/b$.
于是你在考虑, 让 $a, b$ 的第一支放在 $0$ 处, 然后找到最大的区间 $[l, r]$, 其中 $l$ 处有 $b$ 刀片, $r$ 处有 $a$ 刀片.
UOJ310. [UNR #2]黎明前的巧克力
给定 $n$ 个数, 求有多少种方案选择两个不交的集合, 使它们元素的异或和相等.
$n\le 10^6$
等价于求 $\sum_{T\in S} 2^{\vert T\vert}[\mathrm{xor}_i T_i = 0]$, 也就是 $\prod_i (1+2x^{a_i})$.
考虑 $(1+2x^{a_i})$ 的FWT, $1$ 对每个位置贡献 $1$, $a_i$ 对每个位置贡献 $\pm 2$, 位置 $T$ 的符号取决于 $S\cap T$ 的奇偶性. 于是要对所有 $S$ 统计 $\vert T\cap S\vert$ 是偶数. 因为有奇偶性仍然只能用FWT, 考虑做 $\sum_i x^a_i$ 的FWT, 得到的是偶数减奇数, 又因为知道总数就能解出来了.
然后就知道了结果的FWT, 把它IFWT回去即可.
Gym - 102586E
考虑因为是对 $2$ 取模, 那么考虑双射, 把序列翻转, 不相等的已经配对, 只有前半段和后半段相等的没有配对, 递归下去, 则 $2^k$ 的情况只有全部相等的情况映不上. 那么把 $n$ 按二进制拆成若干段, 每一段内部相等, 长度为 $2^k$.
然后数位dp即可: $f_{i, j}$ 表示 $S$ 后 $i$ 位, 对上面进位是 $j$, 因为你长度是 $2^k$ 所以就是正好对应加到一位上, 复杂度是 $ak\log s$. TLE了.
然后对着代码, 猜 $f_{i, j}=0$ 的情况很多, 特判掉卡进去了. 正确的做法是改写成bitset优化.
另一种转化到数位dp的方式是, 设第 $a_i$ 种选了 $c_i$ 个, 方案数就是 $\binom{n}{c_1, c_2, \ldots, c_n} \pmod 2$, 根据卢卡斯定理发现相当于求有多少种方案使得 $c$ 互不相交且或起来上 $n$.
TopCoder 12832 HugeGraph
有一张 $n$ 个点的巨大图, 由一个集合 $d$ 描述, 如果两个点 $i, j$ 满足 $\vert i-j \vert \in d$, 则在 $i, j$ 间连一条无向边. 求连通块个数.
考虑把 $d$ 排序, 然后你可以把 $d_i, i\ge 2$ 替换成 $d_i-d_1$, 也就是 $i\to i+d_1\to i+d_k$. 前 $d_1$ 个点因为不会被作为 $i+d_1$, 所以不需要连新的 $d_i-d_1$.
这样进行一次后, 前 $d_1$ 个点只有一条出边, 所以不会影响连通块数, 直接删了, 问题规模变为 $n-d_i$.
可以把减法换成取模, 就是每次给后面的都膜 $d_1$. 直到仅有一个 $d_i$ 不为 $0$ 或 $n<d_1$
20230520 GDKOI2023TG Day1
Matrix
给定 $n\times n$ 矩阵 $A, B, C$, 判断是否 $A\times B=C \pmod {998244353}$
$n\le 3000$
考虑一个经典题NOI2013向量内积, 随机一个向量乘 $A, B, C$ 判断是否相等. 这里错误率是 $\dfrac{1}{P}$ 所以一个就够了.
Qwq
对于 $n, m, q$, 求排列 $p_n$, 使得 $\forall i\le m, p_i>m; \forall i, p_i\ne i$
$n, m, q\le 2\times 10^5$
利用两个方向递推式+莫队回答二维询问.
考虑固定 $n$ 对于 $m$ 求递推式, 此时变化的是 $m$, 二项式反演得到答案为
$$
\begin{gathered}
\sum_i^{n-2m} (-1)^i \binom{n-2m}{i} (n-m-i)! \
=(n-2m)! [z^m] \sum_i^{n-2m} \dfrac{(-1)^i}{i! } \dfrac{(n-m-i)! }{(n-2m-i)! }\
=(n-2m)! [z^{n-2m}] e^z*(\sum_i \dfrac{(-1)^i(n-m-i)! }{i! }z^i)
\end{gathered}
$$
然后多项式部分是微分有限的, 这表明通过它们的若干阶导数之间存在递推关系, 微分和递推式之间是相互转化的关系. 两个序列做卷积对应多项式相乘, 点积对应递推式相乘. 为了求出相乘后的序列, 考虑 $(AB), (AB)’, (AB)’’\ldots$ 或 $a_nb_n, a_{n+1}b_{n+1}\ldots$, 因为两个分别为 $n, m$ 阶的递推式相乘的到的阶数不超过 $nm$, 所以考虑 $nm$ 个变量, 都把次数/下标数降到最低, 必然出现线性相关, 那么把线性相关的部分就可以得到一个递推式.
$$
\begin{gathered}
A=e^z, A’=A\
b_i=b_{i-1}\cdot -\dfrac{1}{i(n-m-i)}
\Rightarrow\
B=\sum_i \dfrac{(-1)^i(n-m-i)! }{i! }z^i\
B=-(n-m)B’+zB’’, B’’=\dfrac{1}{z}B+\dfrac{1}{n-m}B’
\\
(AB)’=A(B+B’)\
(AB)’’=A(B+2B’+B’’)\
=A((1+\dfrac{1}{z})B+(2+\dfrac{1}{n-m})B’)\
=(1+\dfrac{1}{z})AB+(2+\dfrac{1}{n-m})(AB)’
\end{gathered}
$$
根据这个可以得到沿着 $m$ 的递推式.
再考虑沿着 $n$ 的方向, $f_{n, m}$ 前 $m$ 个没有限制, 剩下的满足 $p_i\ne i$ 的方案数, 这样答案为 $\binom{n-m}{m}m! f_{n-m, m}$.
那么 $m=0$ 时为错排($D$), 考虑 $m\ne 0$ 时, 考虑第一位如果是否选 $1$, 得到 $f_{n, m}=f_{n-1, m-1}+f_{n, m-1}$, 也就是 $F(z)=(1+z)^m D(z)$, 也是微分有限的就冲了.
Graph
给定 $Graph(n, m)$, $a_n$, $C$, 求有多少 $b_n$ 满足 $b_i\in[0, a_i]; \forall u\to v, b_u\ne b_v; \mathrm{Xor}_i b_i =C$
膜998244353, $n\le 15, a_i, C\le 10^{18}$
考虑 $m=0$, 考虑从高到低第一位使得 $\exists b_i\ne a_i$, 那么以后的部分其他 $i$ 怎么选都可以用这个调对, 枚举这一位即可, 复杂度是 $n\log w$.
于是考虑容斥, 钦定若干边相等得到若干连通块, 最终方案相当于所有奇数大小的连通块的 $\min a_i$ 拿出来的答案. 而应该乘上 ${-1}^{边数}$. 但是连通块划分方案远多于 $a$ 的集合, 所以考虑把同一集合的一起计算复杂度就是正确的, 也就需要dp出容斥系数.
先考虑单个连通块的系数, 应该是 $\sum {-1}^{\vert E\vert}$, 其中 $E$ 使得连通块连通. 考虑dp, $f_S$ 先为随便选, 然后枚举 $1$ 所在的连通块 $T$, 减去 $f_T\times 2^{\text{不与T相连的边集}}$, 复杂度 $3^n$.
然后考虑dp系数和, 设 $f_{S, T}$ 表示当前被包含的点集合为 $S$, 有用的 $a_i$ 集合为 $T$, 因为 $T\subseteq S$, 转移时枚举的集合 $U\cap S=\varnothing$, 容易知道复杂度为 $4^n$, 可以通过.
20230527 GDKOI2023TG Day2
Game
给一棵 $n$ 点的树, $q$ 次询问对于给定的 $x, y, z$, 是否能找到3个点两两之间距离分别是 $x, y, z$.
$n, q\le 2\times 10^5$
考虑可以直接求出三个点到这三个点两两路径相交的点的距离, 那么对每个点求出离它最远的三个不同子树的点, 剩下的就是三维偏序.
todo
2023 山东省队互唱 Round 1
给你一颗枪弹!
给定 $k$, $a_n, b_n$, 求有多少种方案把 $a$ 划分成不超过 $k$ 段, 使 $k$ 段归并排序得到 $b$
容易发现如果有解, 所有方案都可以由一个段数最少的划出来, 而这个段数最少的方案就是按照 $b$ 模拟, 如果 $b_i$ 在 $a$ 中前一个元素还没进就一定断开.
然后要判这个情况下是否有解.
然后在此基础上考虑什么情况下一个间隔可以断开, 注意到因为有解, 它只用大于本段中前面所有数即可. 于是求出由多少个必须断的, 多少个可以断的, 然后组合数.
另一种想法是归并不会改变它原来是不是前缀max, 于是所有不是前缀max的位置不能断, 如果这个位置作为前缀max大于前面的则可选, 否则必须断.
复杂度线性或1log(模拟)
关山以北 桦树皮纷飞
交互题, 给定 $m$ 和序列 $c_n$, 初始 $n=1, c_1=0$, 每次可以
add(x)使得添加一个数 $c_{n+1}=c_n+x$, 或者cmp(x, y)返回 $[c_x<c_y]$
log次使用add的复杂度求 $m$.
这个实际上是可以先倍增出大致范围的, 因为如果 $x<m, 2x>m$ 一定有 $2x<2m, 2x-m<x$.
然后的部分是, 确定大致范围后, 考虑当前二分的数是 $x$, 很难注意到, 设当前位置为 $a, b=a+x/2, c=a+x$, 如果判断 $a, b, c$ 大小关系与 $a, b, c$ 同构则 $x<m$, 否则与 $a, c, b$ 同构是 $x>m$, 原因是考虑:
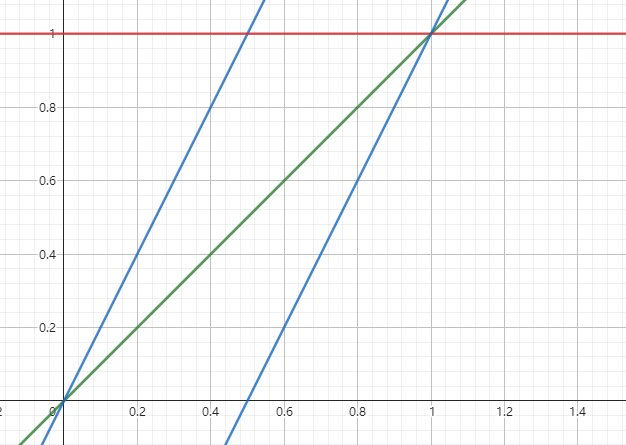
其中蓝线是 $y=2x$ 红线是 $y=m$, 绿线是 $y=x$, 观察 $x=m/2$ 两边的关系即可.
浪漫派的诗人
不会.
ZSTEST230830
A
一眼dp
B
形式化地说, 给定 $k$ 行 $n$ 列的正整数矩阵,
$$
(a_{i, j})_{1 \leq i \leq k, , 1 \leq j \leq n}
$$有 $q$ 个询问任务, 对于每个询问任务 $[l, r]$, 需要计算以下公式:
$$
\sum_{l \leq x \leq y \leq r} F\left(\max_{i=1}^k \left( \min_{j=x}^y a_{i, j} \right)\right)
$$
- 其中 $F(M) = A \oplus ( BM + C)$, $A, B, C$ 是三个非负整数的常数, $\oplus$ 表示二进制按位异或.
$k\le 20, n, q\le 10^5$
如果只有一个序列, 考虑按照从大到小的顺序加点, 并合并两边已经加入的区间, 则每个区间形成的时候恰好是其最小值被插入的时候. 而如果有 $k$ 个序列, 一个区间形成的时候恰好是 $k$ 个序列中这个区间最大的最小值被加入的时刻.
那就简单题了, 直接数点算贡献, 每次矩形加/矩形求和一个2side矩形, 但为了不重复贡献需要把2side矩形拆开并差分成若干3side矩形, 这个过程需要维护右下角阶梯轮廓线. 或者变成矩形覆盖矩形和, 但这个不好差分, 配一个颜色段均摊的话本质相同
C
一条单向环形铁路上有 $k$ 个城市, 分别标号为 $0, 1, \dots , k-1$. 其中, 第 $i$ 个城市可以乘火车到达第 $(i+1)\bmod k$ 个城市. 城市的个数很少.
LCR 想要在这些城市中进行为期 $n$ 天的观光. 第 $1$ 天清晨, LCR 从自家坐火车到达 $0$ 号城市出发开始观光. 每天白天, 每个城市都会举行一些特定的活动, 如果第 $t$ 天的白天 LCR 在 $i$ 号城市里, 那么她会获得 $a_{i, t} (0\le i< k, 1\le t\le n)$ 的效用, 效用是一个非负整数. 除了最后一天之外, 每天傍晚, LCR 可以选择留在当前城市, 或者乘火车移动到下一个相邻城市(从城市 $i$ 移动到城市 $(i+1)\bmod k$). 整个观光旅程的总效用为 $n$ 个白天的效用之和.
LCR 希望她在旅途中恰好坐了特定次数的火车(从家到 $0$ 号城市的一次也算). 因此, 她会询问 $q$ 次, 每次给出一个正整数 $m$, 你需要帮她计算出在恰好坐了 $m$ 次火车的情况下, 观光旅程总效用可能的最大值.
对于 $100%$ 的数据, $1\le m, q\le n\le 10^5, 2\le k\le 5, k\le n, 0\le a_{i, j}\le 10^9$.
有点厉害, 搬运题解:
算法四
对于 $q\le 5$ 的情况, 考虑单次询问的做法.
定义 $F(i)=f[n][i]$, 即 $F(i)$ 表示 $i$ 段对应的答案. 可以证明, 对于任意 $0\le j < k$, $G_j(i)=F(ik+j)$ 关于 $i$ 是一个凸函数.
证明: 考虑 $i-k$ 段的最优解 $A$, 和 $i+k$ 段的最优解 $B$. 用扫描线从 0 扫描到 $n$, 则一开始扫描线左侧 $A, B$ 各有 $0$ 个划分点(指方案中划分相邻两段的位置). 最后, 扫描线左侧 $A, B$ 各有 $i-k-1, i+k-1$ 个划分点. 定义 $t(i)$ 为 $i$ 左侧 $A$ 中的划分点个数减去 $B$ 中的划分点个数. 则 $t(0)=0, t(n)=-2k$. 并且 $t(i)-t(i-1)\in {-1, 0, 1}$. 所以, 必定有一个 $0 < p < n$ 满足 $t(p)=-k$ 且 $t(p)-t(p-1)=-1$.
那么构造两个新方案 $A’, B’$, $A’$ 的划分点是 $A$ 在 $(-\infty, p]$ 的划分点加上 $B$ 在 $(p, \infty)$ 的划分点; $B’$ 的划分点是 $B$ 在 $(-\infty, p]$ 的划分点加上 $A$ 在 $(p, \infty)$ 的划分点. 则, $A’, B’$ 各有 $i-1$ 个划分点, 也就都是 $i$ 段的方案. 并且 $A’, B’$ 的权值和等于 $A, B$ 的权值和. (二者包含的数完全一样)
所以, $A’, B’$ 一定至少有一个权值不大于 $A, B$ 权值的平均值, 另一个权值不小于 $A, B$ 权值的平均值. 按照凸性的定义, 可以证明对于每个 $j$, $G_j(i)$ 是凸函数.
对于单次询问 $m$, 我们可以二分斜率 $W$, 给每一段额外权值 $W$(可正可负), DP 求出全局最优解. 由于凸性, 每个 $i$ 都存在对应的 $W$ 可以找到其最优解. 因为这里还是要记录段数 $\bmod k$ 的值, 所以每次 DP 时间复杂度为 $O(nk)$. 斜率 $W$ 是一个分母为 $k$(注意, 分母是 $k$ 不是 $1$, 因为这里凸函数相邻点距离是 $k$), 绝对值不超过 $nA$ 的数, 其中 $A$ 是 $a_{i, j}$ 的上界.
时间复杂度: $O(nqk\log (Ak))$
预计得分: $30$, 加上之前共 $70$.
算法五(标准算法)
求多个 $m$ 的答案, 我们可以考虑从 $+\infty$ 到 $-\infty$ 枚举斜率 $W$. 这里有 DP 转移 $f[i][j]=\max(f[i-1][j]+a[i][j], f[i-1][(j-1)\bmod k]+a[i][j]+W)$. 可以证明, 在 $W$ 减小的过程中, 对于任意一个 $f[i][j]$, 最优决策(取到 $\max$ 的项)只会变化至多一次, 只能从 $f[i-1][(j-1)\bmod k]+a[i][j]+W$ 到 $f[i-1][j]$.
证明: 只需要证明 $W$ 减小时最优决策不需要从 $f[i-1][j]+a[i][j]$ 变回 $f[i-1][(j-1)\bmod k]+a[i][j]+W$. 首先, 整个问题可以建模成最短路. 反证, 假设某个时刻最优决策必须发生改变, 那么一定存在一个 $W’$ 使得 $f[i-1][j]+a[i][j]$ 和 $f[i-1][(j-1)\bmod k]+a[i][j]+W’$ 在这个时刻是相等的, 且在 $W’-\epsilon$ 时后者严格更优. 那么这时后者对应的最优方案的段数(等于 $f[0][0]$ 到 $f[i][j]$ 最短路上 $+W$ 的次数)一定严格小于前者. 所以, 考虑从 $i-1$ 扫描到 $0$, 初始时前者对应方案在扫描线之后的段数比后者对应方案在扫描线之后的段数少 $1$, 但最后却严格多于后者至少 $k$, 所以一定有某个时刻两者在扫描线上相交. 所以一定存在 $0 < p < i-1$ 满足某个 $f[p][. ]$ 到 $f[i][j]$ 有两个段数相同的不同转移(两条 $+W$ 次数相等的不同最短路). 考虑把 $W’-\epsilon$ 的方案的 $f[p][. ]$ 到 $f[i][j]$ 的部分替换成从 $f[i-1][j]+a[i][j]$ 转移的, 这样段数不变. 所以 $W’-\epsilon$ 时一定也存在一个从 $f[i-1][j]+a[i][j]$ 转移的最优方案. 矛盾!
所以, 这 $nk$ 个决策点各只会变化最多一次. 考虑维护这些变化.
任何时刻, 我们让 $(i, j)$ 向它的最优决策的上一次状态($(i-1, j)$ 或者 $(i-1, (j-1)\bmod k)$)连边. 显然, 这形成一棵有根树(就是最短路径树), 且合法点 $(i, j)$ 的深度一定为 $i$.
我们用线段树维护最短路径树的区间信息. 首先, 对于每个区间, 为了维护右端点当前的最优解(到根路径长), 需要记录区间右端点的每个点在区间左端点前一层的祖先 $anc(i)$ 以及到这个祖先的路径长度(一个以 $W$ 为自变量的一次函数, 换言之, 当前最短路的段数和效用). 其次, 为了维护 $W$ 减小时下次转移最早的变化, 需要记录 $LCA((i-1, j), (i-1, (j-1)\bmod k))$ 在区间内的所有点 $(i, j)$ 中最小的最短路效用差(段数差一定是 $k$, 所以不需要记录). 以及对于 $LCA((i-1, j), (i-1, (j-1)\bmod k))$ 不在区间内的点 $(i, j)$, 对于每个不同的 $(anc((i-1, j)), anc((i-1, (j-1)\bmod k)))$ 对, 记录最小的最短路效用差(因为段数差是一个定值, 所以不需要记录).
任何时候, 任何一个区间中不同的 $(anc((i-1, j)), anc((i-1, (j-1)\bmod k)))$ 的对数不会超过 $2k$. 考虑把决策树画在一个高度 $n$, 周长 $k$ 的圆柱面上, 那么区间左端点每个点在区间内的子树对应圆柱面上的一个平面区域. 通过平面图的性质可以证明左端点相邻的面的接缝即平面图边数不超过 $2k$ 即左端点面数的 $2$ 倍.
这样, 我们用线段树支持单点修改最优决策, 维护扫描线 $W$ 减小时下次最优决策改变位置. 每次从线段树中取出下一个最优决策改变的位置(全局改变需要的 $W$ 的最大值), 然后修改那个位置的决策即可. 初始以及每次修改后需要用全局最右侧每个点到根路径长度更新对应段数的答案.
一共 $O(nk)$ 次操作, 每次时间复杂度 $O(k\log n)$.
时间复杂度: $O(nk^2\log n)$
预计得分: $100$
凸性配合wqs二分得到算法4, 但算法5还是很厉害.
获得了更简单的做法!
考虑 $f_{l, r, x, y, t}$ 表示从 $l$ 天到第 $r$ 天, 一开始在城市 $x$ 第 $r+1$ 天在城市 $y$, 一共经过 $k$ 轮的最大收益. 算法四结论有 $F_{l, r, x, y}(t)$ 是凸的, 于是直接分治着合并凸包就行了. 复杂度合并凸包要枚举 $x, y, z$ 以合并 $f_{l, mid, x, y}$ 和 $f_{mid+1, r, y, z}$, 而 $t$ 实际上是 $len/k$ 种, 最后和正解一样是 $nk^2\log n$
有点类似 IOI13 Wombats的dp设法.
最后还是要想如何发现凸性, 可能本来会猜对 $m$ 有凸性, 然后被不同的城市干爆了, 于是弱化到固定城市后有凸性.
[trick] 大函数没凸性细分后有凸性
ZSTEST230831
A
基本就是CF Make It One, 不过范围是 $4\times 10^6$, 用gcd卷积那一套即可. 复杂度应该能到 $v(\log \log v)^2$. 瓶颈是二分答案里面快速幂.
B

$n\le 10^6$
对于每个缝隙, 找到最近的可以切断的位置(这个区间内A和B的值集合相等), 然后连边形成若干个缝隙的环, 每个环上任意断数数即可.
然后为了判断可以切断需要集合hash.
C
原题是 CF1210G/CF1229F

$n\le 10^6$
赛时写了个网络流.
正解就是先断环, dp, 设 $f_{i, j}$ 表示前 $i$ 个已经满足, $i$ 向 $i+1$ 传了 $j$ 个, 然后发现 $f_i$ 是关于 $j$ 的凸函数, 上一套 slope trick维护转移, 搭配wqs二分 $n$ 到 $1$ 传了多少.
转移时发现每次是对 $f_i$ 进行平移, 然后添加一段斜率为 $0$ 的部分, 然后加上函数 $\vert x\vert$, 可以用平衡树以斜率为键实现区间加, 但更好的方法是用对顶堆维护斜率为负的部分和正的部分以及当前位置的值即可.
ZSTEST230902
A
考虑直接把 $k$ 的答案写出来, $ans_k=\sum_i \lceil \dfrac{h_i}{k} \rceil k - h_i$, 那么 $\lceil \dfrac{h_i}{k}\rceil=\lfloor \dfrac{h_i-1}{k}\rfloor+1$ 转化成下取整, 那么显然对任意一个 $i$ 都是 $\sqrt V$ 段函数, 总共是 $n\sqrt V$ 段函数, 考虑直接让 $k=1$, 用堆维护当前 $k$ 所在的 $n$ 个段的 $n$ 个右端点即可. 复杂度 $n\sqrt V\log n$
B
考虑这是简单扫描线, 每个B获得的元素 $(a, b, c)$ 拆成3个立方体, 最后相当于求立方体体积并, 但注意到每个立方体只有两维有限制, 考虑计算合法数量, 按照 $c$ 扫描线, 那么把所有 $c$ 上没有限制的先画到平面上, 然后剩下的每个矩形相当于限制当 $c\le c_i$ 时 $a\ge a_i$ 或 $b\ge b_i$, 那么可以相当于在刚才的平面上一个矩形查询. 于是最后就是, 在一个平面上2side矩形加矩形和, 再上一个扫描线即可.
C
预处理出每个位置往前第一个和为 $0$ 的矩形, 有一个显然的 $n^2$ dp, 设 $f_{i, j}$ 表示第一行前 $i$ 个和第二行前 $j$ 个的答案, 那么注意到如果 $f_{i, j}, f_{i, k}$ 是分别最小的 $j, k$ 使得 $f_{i, j}=f_{i, i}+1, f_{i, k}=f_{i, i}+2$, 那么可以只保留 $f_{i, j}$, 考虑如果第一行中 $[i, j]$ 中与一个矩形无交, 那么所有从 $i, k$ 的转移都可以由 $j, j$ 转走, 如果有交, 那么如果原应由 $f_{i, k}\to f_{i’, k}$, 应该存在状态 $f_{i’, j}$, 其中 $i’$ 是最小的满足 $f_{i’, j}=f_{j, j}+1$ 的位置, 于是只保留所有的 $f_{i, i}, f_{i, j}, f_{j, i}$ 即可完成转移. 至于要保留哪些, 显然 $f_{i, j}$ 就是 $f_{i, i}$ 往后第一个矩形结尾, 可以预处理.
潍坊一中 2023 秋提高级友好学校赛前联测 1
260 RK 16
DWT RK 1 /bx
T1, T2简单题, T4是CF1119F(不会了菜了)
T3
Mystia 想搭一座跨过河的桥, 来方便她取得食材.
河是一条无限长的宽度为 $W$ 的直线, 所有在坐标系中符合 $0\le y\le W$ 的点都属于这条河流.
河面上有 $N$ 个木桩, 附近的杂货店可以买到 $M$ 种可以使用的木头圆盘, 第 $k$ 个木桩的坐标为 $(X_k, Y_k)$. 第 $k$ 种圆盘半径为 $R_k$, 每一块的价格为 $C_k$.
她可以买任意种任意多的圆盘, 把它们放到河面上. 每一个圆盘的中心都必须为某一个木桩的位置. 而且, 某些圆盘的一部分可以在地面上, 即 $y<0$ 或 $y>W$.
Mystia 只能在河两岸或圆盘上移动, 两岸即直线 $y=0$ 或直线 $y=W$, 也可以从一个位置移动到另一个与其相切或相交的圆盘.
请问她修建一座可以从直线 $y=0$ 到直线 $y=W$ 走过去的圆盘桥的最小花费是多少?
复杂度 $n^2\min (m, R)$
首先要做到 $n^2m\log nm$ 是简单的建图题, 直接拆点前后缀优化暴力连边即可.
考虑不拆点, 设 $f_{i, j}$ 为 $i$ 上盘子种类为 $j$ 情况下 $1$ 到 $i$ 的距离, 那么模拟dij的过程, 记 $g_i=\min_j f_{i, j}$, 改为每次选 $g_i$ 最小的点, 用它更新其他所有的 $f_{k, l}$, 更新的时候直接双指针容易做到 $O(m)$, 但是这个最短路看起来是不对的, 考虑证明, 如果松弛顺序有问题, 只可能因为两个桩子 $i$, $j$, 当前 $g_i<g_j$, $i$, $j$ 都在最短路上且 $i$ 比 $j$ 靠后, 但此时绕道走 $j$ 唯一目的只能上让 $i$ 换一个更大的盘子, 那么如果其盘子由 $x$ 换到 $y$, 直接更改 $i$ 的盘子只有 $f_{i, x}-c_x+c_y$, 而j过去至少要更新到 $g_j+c_x$, 于是此时一定不会让 $j$ 去松弛 $i$, 更新顺序就是对的了.
出题人impossible打成impossib1e, 被刺杀了(没和R取min, 被刺杀了
信友队CSP-S 2023 复赛模拟赛
A
给出 $n\times m$ 的 $01$ 矩阵, 求有多少个正方形满足四个顶点都是 $1$, 正方形可以斜着.
$n, m\le 500$, 5s
挺见鬼的, 容易想到把斜着的正方形变成证明勾股定理的那个图, 也就是一个小正方形, 四个顶点分别向四个方向延伸相同长度位置都是 $1$. 那么枚举这个小正方形然后bitset即可 $n^4/w$, 但是感觉卡的很紧一直不敢写.
B
考虑出售一种商品, 有 $m$ 种卖法.
第 $j$ 种卖法将卖出其中 $a_j$ 个, 收 $b_j$ 的钱.
对所有 $1\le i < m$, $a_i$ 是 $a_{i+1}$ 的因数; 且保证 $a_1=1$.
假设买恰好 $n$ 个物品最少要花 $f(n)$ 的钱. 你可以同时使用多种买法.
现在 $q$ 组询问, 每次给定 $n$, 要求出 $\sum\limits_{i=0}^{m-1} f(i)$.
由于答案可能很大, 请对 $2^{64}$ 取模.
$m, q\le 10^5, n\le 10^{18}$
首先按性价比排序, 性价比不优的都删了, 现在性价比递增, 最多剩 $\log n$ 个. 于是统计每个被用了多少次, 最后相当于要求 $\sum_{i=1}^n \dfrac{i}{a_k}$, 等差数列求和即可.
C
给定一张 $n$ 个点 $m$ 条边的无向连通图, 点标号 $0\sim n-1$, 其中前 $c$ 个点为关键点.
每个点有点权 $a_p$, 边有边权 $w_e$. 关键点还额外有一个权值 $b_p$.
你要选定一个起点, 从起点开始, 中间经过至少 $t$ 个关键点(允许重复经过一个关键点, 但只统计一次), 最后回到起点. 起点可以是关键点, 也可以不是. 可以待在起点不移动, 但那样所统计的关键点仅包括起点本身.
规定该方案的代价为 $\text{路径长度}+a_{\text{起点}}+\sum\limits_{q\in\text{所有被经过的关键点}} b_q$, 如果一个关键点被多次经过也只统计一次.
你要对 $t=1, 2, 3, \dots, c$ 求出最小代价.
$c\le 20, n\le 1\times 10^5, m\le 3\times 10^5$
还算比较好想吧. 容易想到先对每个关键点跑一遍dij, 处理出 $d_{i, j, 0/1}$ 表示关键点 $i$ 到关键点 $j$, 其中是否有一个点加上了 $a$(作为起点)的最小代价. 同时注意跑最短路时不能用除起点以外的关键点松弛, 否则一条经过某几个关键点的路径会漏算 $b$.
然后这个 $20$ 显然让你dp, 想到设 $f_{S, i, 0/1}$ 表示当前走过的关键点集合为 $S$, 当前在 $i$, 有没有已经选择一个起点, 则每次要么枚举一个点 $k$ 从 $f_{S/i, k, 0/1}$ 转移过来, 要么由 $f_{S, j, 0/1}$ 转移过来, 后面这个需要跑一个最短路. dp的复杂度是 $c^22^c$, 但是要对每个起点跑一遍就爆炸了.
因为最后让你选一个环, 可以把其中任意一个点当作环的起点, 考虑钦点 $S$ 中编号最小的点为起点, 每次转移的时候不能把起点转移没就行了. 最后复杂度 $c^22^c$
D
我们称字符串 $A$ 对 $B$ 的相对代价, 为 $A$ 的 Border 中不是 $B$ 的 Border 的字符串的长度之和.
我们称字符串 $A$ 和 $B$ 的绝对代价, 为 $A$ 对 $B$ 的相对代价和 $B$ 对 $A$ 的相对代价中较大的一个, 记为 $f(A, B)$.
我们称长度为 $n$ 的字符串 $S$ 的刻板度为其每两个后缀的绝对代价之和, 也即
$g(S) = \sum\limits_{i=0}^{n-1}\sum\limits_{j=i+1}^{n-1} f(S_{i\sim n-1}, S_{j\sim n-1})$
现在给你一个长度为 $n$ 的字符串 $S$, 你要对其最长的 $c$ 个后缀子串 $S’$, 求出 $S’$ 的刻板度; 即, 你需要对每个 $0\leq l<c$ 求出
$h_l(S) = g(S_{l\sim n-1}) = \sum\limits_{i=l}^{n-1}\sum\limits_{j=i+1}^{n-1} f(S_{i\sim n-1}, S_{j\sim n-1})$
由于答案可能很大, 只需输出对 $2^{64}$ 取模的结果.
首先考虑对于同一个字符串的两个后缀, 这个绝对代价是什么. 那么考虑反着跑KMP得到每个后缀的border, 然后 $i$ 向 $border_i$ 连边得到一棵树, 记 $dep_u$ 为根到 $u$ 的链上的字符串总长和, 那么绝对代价就是 $\max dep_a, dep_b -\mathrm{lca}(a, b)$. 感觉这个模型应该很经典但我没做过这种啊()
那么考虑怎么做 $c=1$, 把刚才那个东西分开做, 则一部分要求每个点是多少个点的lca, 可以是 $\sum (siz_u^2-\sum_{v\in son_u} siz_v^2)dep_u=\sum siz_u^2(dep_u-dep_{fa})$, 一部分求比这个点 $dep$ 小的有多少个即可.
那么现在 $c\ne 1$, 考虑从最短的那个后缀开始, 每次在最前面加一个字符, 也就是树上一个叶子, 考虑答案增加了多少. 那么对于刚才分开的两部分, 第二部分是容易的, 直接统计比这个点小的点的个数和比它大的点的 $dep$ 和. 对于第一部分, 这个点让它到根的链上每个点 $siz$ 增加了 $1$, 增加量就是 $\sum (1+2siz_u)(dep_u-dep_{fa})$, 用线段树+静态lct是单log了, 但这很见鬼. 考虑代替方法, 每个点开一个线段树, 其中下标 $i$ 表示加入第 $i$ 个点时的新增贡献, 那么每次把儿子合并, 然后对线段树区间加一次函数, 这就可做了.
这个失配树的trick居然没见过, 菜了.
Public NOIP Round #6 (Div. 1, 提高)
A
给定一个长度为 $n$ 的非负整数序列 $[a_1, \ldots, a_n]$, 求其中某个子序列 $[a_{i_1}, a_{i_2}, \ldots, a_{i_k}]$ $(1\leq i_1<i_2<\cdots<i_k\leq n)$, 使得 $\sum_{j=1}^{k-1}(a_{i_j}\text{ and } a_{i_j+1})$ 最大. 其中, $\text{and}$ 是指二进制按位与.
$n\le 10^6, a_i\le 10^{12}$
容易想到 $n^2$ 的dp, 考虑优化, 注意到看起来多选几个大概率比少选优, 然后发现对于最高位为 $k$ 的所有 $a_i$ 只有最后一个是可能被转移的, 因为不然倒数第二个转移到最后一个, 最后一个转移到当前一定比倒数第二个转移到当前优. 复杂度单 $log$
看到位运算要想位, 包括最高位, 拆位, 进位条件.
B
你有 $n$ 个任务需要完成, 第 $i$ 个任务需要 $t_i$ 天. 但人的寿命有限, 你只剩下 $c$ 天了.
磨刀不误砍柴工, 你可以花 $1$ 天时间对第 $i$ 个任务进行深入思考, 那么它所需的时间会减少 $d_i$ 天. 特别的, 如果时间被减为零或负数, 这个任务就能被瞬间完成. 但人的灵感有限, 在一次生命里每个任务只能被深入思考一次.
你可以复活, 每次复活会再给你带来 $c$ 天. 之前的深入思考的结果会一直保留, 不会因复活而消失.
求出你最少需要复活多少次, 才能在最后一条命把所有任务都完成. 你可以认为在最后一条命之前你并不能做任务, 只能对任务进行思考, 而在最后一条命既可以思考也可以做任务.
$1\leq T\leq 1000$, $1\leq \sum n\leq 2\times10^5$, $1\leq c\leq 10^9$, $1\leq d_i\leq t_i\leq 10^9$.
二分答案, 现在考虑前面怎么分配思考, 发现对于一个任务来说不断对其思考收益递减, 于是因为凸性这是经典的贪心, 每次选收益最大的即可. 又因为直接做 $c\cdot ans$ 很大, 你应该把每个任务都先缩减到 $2d_i$ 以内, 然后再贪心救行.
C
给定一个 $n$ 个点 $m$ 条边的简单无向连通图.
有 $q$ 次询问, 每次给定两个不同的点 $x$ 和 $y$, 你可以从 $x$ 出发在图上任意游走, 直到走到 $y$ 时结束, 且除了开始和结束以外不允许走到 $x$ 和 $y$. 求出有多少个点 $z$ 使得存在一个游走方案能经过 $z$, 包括 $x$ 和 $y$. 注意你走的路径可以不是简单路径, 唯一的限制是不能重复经过 $x$ 和 $y$.
$1\leq T\leq 1000$ $1\leq \sum n\leq 2\times10^5$ $1\leq \sum m\leq 5\times10^5$ $1\leq \sum q\leq 5\times10^5$
圆方树!
D
给定排列 $a_n$, 希望把他排序, 每次可以把排列分成若干段然后段间reverse, 段内顺序保持不变.
$n\le 2\times 10^4$, 次数限制 $90$
好厉害构造, 考虑只有 $01$ 的情况, 按照01|0|10|1|01|0|10|1每次可以把连续段数搞成 $1/3$, 然后对值分治, 把大于 $mid$ 的看作 $1$, 其他看作 $0$, 最后复杂度是俩log
潍坊一中 2023 秋提高级友好学校赛前联测 2
T1
给 $n$ 个区间求嵌套最大层数
直接dp, 上个线段树. 但是区间排序没排右端点相等的左端点挂了35/fn
T2
简单dp
T3
乐孤星和 WA90 准备联合参加下一次的 NOB(National Olympiad in Badminton).
他们想要在一场比赛中击回对手打出的所有球从而赢得比赛, 因为 WA90 非常强, 所以可以预先知道对手打出的每一个球的位置, 他们想要计算一下打败对手需要多认真.
形式化的, 我们将羽毛球场比作一个一维数轴, 不考虑高度的限制. 起初两个人都在数轴的原点, 两个人的移动是独立的, 并且可以互相越过或处于同一位置. 任意时刻, 他们可以以不超过 $V$ 的速度移动或处于静止状态.
现在他们预测到了对手将能打出 $n$ 次球, 第 $i$ 个球将于时刻 $t_i$ 飞到位置 $x_i$, 也就是说在时刻 $t_i$ 至少有一个人位于 $x_i$ 才能击回第 $i$ 个球. 现在请你求出两个人若想击回所有的球, 速度上限 $V$ 至少是多少.
对于全部数据, $1 \leq n \leq 10^5$, $1 \leq t \leq 10^9$, $- 10^6 \leq x \leq 10^6$.
简单dp, 但是写飞了TLE 50, 把一个set换成vector过了.
显然二分答案判定, 那么设 $f_{i, j}$ 表示当一个人处理完第 $i$ 次时, 另一个人最近一次处理的是第 $j$ 次的情况是否可行, 那么显然有
$$
f_{i, j}=
\begin{cases}
f_{i-1, j}=[i-1\to i], if\ j\notin {i, i-1}\
f_{i-1, k}\ \mathrm{and}\ [k\to i], if\ j=i-1\
f_{i-1, k}\ \mathrm{and}\ [k\to i]\ \mathrm{and}\ [i-1\to i], if\ j=i
\end{cases}
$$
其中 $[k\to i]$ 表示
于是数据结构维护dp即可, 发现要求 $f_{i-1}$ 中是否有一个点可以到达 $i$. 考虑把点 $(t, x)$ 画到平面上, 于是你要求两个斜率固定直线之间的点的数量, 支持删点加点, 上线段树/bit即可.
还可以更快! 其实一开始猜的就是对于某一时刻的 $i$, $j$ 的存在范围是一个区间, 于是用这个dp直接做到 $n\log V$.
T4
Alice 和 Bob 在玩游戏, 他们面前有一个长度为 $n$ 的正整数序列 $a$, 一共有 $q$ 次游戏, 每轮游戏给定 $[l, r]$, Alice 会在 $[l, r]$ 中挑选 $k$ 个数, Bob 会计算这些数的 $\gcd$ 作为自己的得分. Bob 想要知道在 Alice 的所有选择方案中, 他能得到的最大得分是多少. 因为 Alice 比较贪心所以她会选择比较多的数, 因此在此题中 $k\geq (r-l+1)-3$.
对于全部数据, $1\leq n, q\leq 10^5, \max(1, (r-l+1)-3)\leq k\leq (r-l+1), 1\leq a_i\leq 10^{18}$.
众所周知从一个点开始的区间的gcd只有 $\log V$ 段, 那么直接预处理每个位置开始的 $gcd$ 段, $\log^3 V$ 枚举删的点(一定是段的起点)再乘上 $\log V$ 合并就过了.
山东省实验中学 2023 秋提高级友好学校赛前联测 3
A是简单题, B是模版矩阵优化dp
C
给定一个长度为 $n$ 的 01 串, 你需要将它划分成若干段, 每一段的长度都不超过 $m$, 且满足以下两种条件之一:
- 这个段中全部为 $0$ 或全部为 $1$.
- 这个段中 $0, 1$ 数量之差不超过 $k$.
你需要求出该 01 串合法的划分最少要多少段.
对于 $100%$ 的数据, 满足 $1 \le n, m, k \le 10^7$
容易想到简单的线段树优化dp做到单log: $f_i$ 表示前 $i$ 个最少分几段, 另外套路的 $s$ 表示把 $0$ 当做 $-1$ 之后的前缀和, 然后就是找 $j\ge i-m, s_j\in [s_i-k, s_i+k]$ 的最小 $f_j$, 于是线段树维护 $j\ge i-m$ 中的部分, 在每个 $v$ 开堆维护所有 $s_j=v$ 的 $f_j$, 使得在删掉 $j<i-m$ 的决策时知道改改成啥.
然后观察性质, 对于任意两个 $i<j, i, j$ 属于同一个堆, $f_i-f_j=1$, 于是你只要维护堆里面最大的, 次大的位置和最大值就行了, 替换掉堆.
然后要替换掉线段树, 发现要在每个位置最多变化 $1$ 的序列上, 每次左右端点各移动 $1$ 的区间求最小值, 且值域 $O(n)$, 于是可以套路的用桶维护最小值个数, 处理左右端点, 而当删除时最小值数量减到 $1$ 时, 最小值 $+1$ 的位置如果是 $0$ 也不需要继续找, 因为一定可以通过全为 $0/1$ 转移成 $f_{i-1}+1$ 也就是原来最小值 $+1$ 转移过来.
[trick] 每个位置变化 $1$, 左右端点每次移动 $1$ 的求区间最小值
D
给定一个长度为 $N$ 的序列 $A$. 对于一个子序列, 若任意两个在子序列中相邻的元素 $A_x, A_y (x<y)$, 都满足 $A_x < A_y$, 且原序列的> 区间 $[x, y)$ 中不存在严格大于 $A_x$ 的值, 那么我们就说这个子序列是”贪心上升”的.
定义一个子序列的权值为子序列中所有元素的和, 给定 $Q$ 次询问, 每次询问给定一个区间 $[L, R]$ , 请你求出这个区间中权值最大的贪心上升子序> 列的权值是多少.
对于所有数据, 保证满足 $0 \le a_i, S \le 10^9, T \in [0, 1]$.
直接找到区间中第一个最大值 $A_x$, 则全局中 $i\in [l, x]$ 开始往后找到的最大子序列长度 $f_i$ 和限制了区间之后找到的只差一个 $f_x-1$, 因为走到 $x$ 之后的剩下都相同了. 而 $i\in [x+1, r]$ 可以找以它结尾的最大长度 $g_i$, 那么它一定起始于 $x$ 之后也就一定在区间里. 于是最后只需要预处理 $f, g$ 和最大值的ST表, 查询的时候就只有RMQ了.
[think] 使得局部的答案就是全局的答案的子集.
山东省聊城第一中学 2023 秋提高级友好学校赛前联测 4
A.
今年, C 教授举办了一个春令营. 春令营拥有 $n$ 个学生, C 教授在春令营里开设了 $m$ 个技能培训.
春令营结束前, C 教授想选出一些学生组成兴趣小组进行实地考察.
第 $i$ 个学生可以用两个数刻画: $a_i, b_i$. 其中 $b_i$ 表示第 $i$ 个学生的能力值; $a_i$ 表示第 $i$ 个学生会的技能, 如果在二进制下 $a_i$ 从低到高数第 $j$ 位> 为 $1$, 说明该学生会第 $j$ 项技能.
对于两个学生 $x, y$, 如果存在一项技能 $x$ 会但是 $y$ 不会, $x$ 就会认为自己比 $y$ 强.
为了避免混乱, C 教授组成的小组里面不能有一个人认为自己比组里其他学生都强, 且小组最少要有两个人. 在此基础上, C 教授希望选出的小组能力值 $b_i$ 之和尽量大. 输出能力> 值之和最大值.
如果无法选出这样一个小组, 输出 $-1$.
$n\le 7000, m\le 60$
考虑出现过两次以上的 $a$ 的对应元素都可以加上去(他们相互不认为厉害), 对于其他元素 $x$ 不认为自己比 $y$ 强当且仅当 $a_x\subseteq a_y$, 所以其他元素必须被这些相等的元素包含, 把被包含的全部加上即可.
B.
求串 $s$ 中形如 $t=\texttt{114514}$ 的子序列 $q$ 的个数, 形如指长度相等, 且 $\forall i, j\ [t_i=t_j]=[q_i=q_j]$
$n\le 10^6, m\le 62$
发现如果我们要先数若干 $t$ 的子串拼起来, 如 $\texttt{114}$ 和 $\texttt{14}$, 那么我们无法保证它们对应的 $\texttt{1, 4}$ 对应相等.
另一个思路是枚举三种字符的实际值, 复杂度爆炸, 但枚举两种, 每次关于两种字符数量之和的做复杂度是 $nm$ 可以接受, 于是枚举 $\texttt{1}\texttt{4}$ 分别是谁, 数出每个 $\texttt{4}$ 前的 $\texttt{1}$ 和每个 $\texttt{1}$ 后的 $\texttt{4}$ 的个数即可合并答案($\texttt{5}$ 的方案就是 $\texttt{1}$ 和 $\texttt{4}$ 之间与它们不相等的数的个数)
C.
给定一个长度为 $n$ 的 0-1 串 $s_0s_1s_2\cdots s_{n-1}$, 你需要通过不超过 $L$ 次操作将其变为目标串 $t_0t_1t_2\cdots t_{n-1}$.
操作具体如下:
- 首先给出一个整数 $0\le k\le L$.注意并没有要求 $\bm {k\le n}$.
- 如果 $k>0$, 接下来 $k$ 次, 第 $i$ 次操作你需要给出一个整数 $p\in[0, n-1]$, 并依次将 $s_{p}, s_{(p+1)\bmod n}, s_{(p+2)\bmod n}, s_{(p+3)\bmod n}, > \cdots, s_{(p+i-1)\bmod n}$(即一个长度为 $i$ 的区间)异或 $1$.
请你构造一个合法的操作, 或报告不存在可以在 $L$ 次内完成要求的操作方案.
| $n$ | $L$ | 子任务编号 | 分数 |
|: -: |: -: |: -: |: -: |
| $\le 5$ | $=400$ | $0$ | $15$ |
| $\le 9999$ | $=5\times 10^5$ | $1$ | $5$ |
| $\le 9999$ | $=10^4+1$ | $2$ | $15$ |
| $\le 9999$ | $=9999$ | $3$ | $5$ |
| $\le 99999$ | $=5\times 10^5$ | $4$ | $5$ |
| $\le 99999$ | $=2\times 10^5$ | $5$ | $10$ |
| $\le 99999$ | $=10^5+1$ | $6$ | $10$ |
| $\le 99999$ | $=10^5$ | $7$ | $20$ |
| $\le 99999$ | $=99999$ | $8$ | $15$ |对于所有数据, $n\le99999, 1\le n\le L \le 5\times 10^5$, $s$ 和 $t$ 仅由 $0$ 和 $1$ 构成.
注意到两次让一位相同并不影响其他位是好做的. 那么我们会做 $L\ge 2c$ 的数据, 其中 $c=\sum [s_i\ne t_i]$, 注意到 $L=n$ 的范围内 $L$ 一定是奇数, 于是对于 $L<2c$ 的点你可以直接用 $p=n$ 的一次整体翻转剩下的直接做.
D.
求 $Graph(n, m)$ 用 $k$ 种颜色染色的方案数, 要求一条边相连的两点颜色不同.
$n\le 10^5, m\le n+3$

只取其中”点数很多的话”后面的部分即可.
山东师大附中2023 秋提高级友好学校赛前联测 5
A.
给定排列 $p_n$, 每次循环右移 $k$ 位或将其置换一次, 置换指 $p’_{p_i}=i$.
$n\le 10^5$
考虑置换实际上是交换一个点的值和下标, 那么你记录 $(a, b)$ 表示 $a$ 位置是 $b$, 则循环右移是模意义下加, 置换是交换 $a, b$, 于是可以合并操作了.
B.
给定有向图 $Graph(n, m)$, 若 $u$ 可以到达 $v$ 则 $u$ 和 $v$ 不能在同一组, 求整张图最少被划分到几个组.
容易发现它就是让你求最长链状物, 如果没有环是最长链, 有环是缩点后点权为SCC大小后的最长链.
C.
现在有 $n$ 个数, 其中第 $i$ 个数等于 $2^{a_i}\times3^{b_i}$.
对于所有的非空子集, 求出它们的最小公倍数, 并且求和. 求这个和对 $10^9+7$ 取模的结果.
对于 $100%$ 的数据, 满足 $1\le n\le10^5, 0\le a_i, b_i\le10^9$.
这个题和昨天南外(NOIP2023模拟赛48)T4好像啊.
考虑设 $f_i$ 表示 $lcm$ 的 $2$ 上指数小于等于 $i$ 的情况下, 所有lcm的 $3$ 的次幂之和, 考虑如何计算 $f_i$, 现在只加入 $2$ 上指数小于 $i$ 的数, 那么若 $3^k$ 有 $c_k$ 个, $s_k=\sum_{l<k} c_l$, 答案就是 $\sum_k (2^{c_k}-1)2^{s_k}$, 线段树维护即可.
D.
有一个数列 $a_1, a_2, \ldots, a_n$, 它是 $1, 2, \ldots, n$ 的一个排列.
现在你想对这个数列进行一些变换: 每一次可以选择一对 $i, j$, 满足 $1\le i<j\le n$ 且 $a_i>a_j$, 然后将 $a_i$ 和 $a_j$ 交换.
问通过若干次(可以 $0$ 次)变换, 能得到多少种不同的排列. 输出答案对 $10^9+7$ 取模的结果.
$n\le 30$
有点难想?
如果是 $01$ 序列是会做的, 就要求所有 $1$ 的位置分别比原序列 $1$ 的位置靠右即可. 那么可以把问题转化对每个 $k$, 把大于 $k$ 的当成 $1$, 其他是 $0$, 的情况下均合法的数量. 于是可以dp, 设 $f_S$ 表示当前 $01$ 集合是 $S$ 的方案数, $\vert S\vert$ 就是 $n-k$, 每次从 $S$ 转移到 $S\vert 2^k$ 即可
威海实验 2023 秋提高级友好学校赛前联测 7
A.
有 $n$ 个矿堆
初始时第 $i$ 个矿堆有 $v_i$ 价值开采, 每次开采价值减少 $w_i$
即这一次得到的价值是 $v_i$, 下一次 $v_i\to(v_i-w_i)$ .
求出开采 $k$ 次的开采价值最大值.
对于全部的数据 $1\le v_i, w_i\le 10^{18}$
和CF1661F, CF1344D一样的trick, 凸的二分优化贪心即可
见greedy
B.
给你一个 $01$ 序列 , 长度为 $n$ .
每次你可以选择 $1$ 附近距离小于等于 $q$ 的一个 $0$ 并把它改为 $1$ .
求把整个序列都标记成 $1$ 的操作方案数取模 $10^9+7$ 的结果.
保证至少存在一种操作方案.
$n\le 10^6, q\le 100$
考虑一堆 $0$ 被两个 $1$ 夹在中间, 那么更远的 $1$ 都没有用了, 所以答案其实就是每一段连续 $0$ 的答案.
而这个可以很好地转移啊, 枚举第一个填的 $1$ 的位置即可. 复杂度 $nq$
C.
给一棵树, 上面有 $n$ 对点, 每对点上权值, 每次对链包含的点减(包含一个点就给点对减去一次, 包含两个点减两次), 对每个 $i$ 求点对被第一次减成 $0$ 的代价.
$n, q\le 2\times 10^5$
问题就是求每个点对结束贡献的时间, 这不是我们的减半警报器吗?
复杂度 $n\log n\log V$
可以树上差分, 离线, 转成矩形加(dfn, time)然后以dfn为版本维用主席树维护, 复杂度可以单log啊
D.
给定树, 求路径上有多少点对 $a, b$ 满足存在 $k$ 使得 $\lfloor \dfrac{w_a}{k}\rfloor=w_b$
$w$ 互不相同, $n, q, w_i\le 5\times 10^4$
有 $n\sqrt n$ 对满足条件的点, 直接根号平衡复杂度扫描线秒了.
淀粉质也可以线性空间复杂度带log.
然后可以搞二次离线莫对之类的东西搞成空间线性的根号log并不依赖互不相同.
信友队 2023 NOIP 模拟赛
A. 呜
给定 $n\times m$ 01矩阵, 求有多少个子矩形满足翻转左上角一个全 $1$ 正方形后是全 $0$ 的, 不能不翻.
$n, m\le 2000$
你以为这个答案是 $n^4$ 级的, 其实它是 $n^3$ 级的.
发现如果枚举左上角或者正方形的右下角, 另一边相当于要求子矩形内的全 $0$ 矩形个数, 感觉很见鬼, 但如果枚举右上角, 发现其对应的左上角是唯一的, 于是就做完了. 复杂度 $n^2$ 可能带log.
[think] 这种对某种性质的结构计数的时候, 你一开始猜的关键位置(中间, 左上角)不一定是关键位置, 想不出来的话就要考虑其他位置. 另外就是01矩阵中的均摊性质, 点对能形成的匹配总个数一定但具体到一个点可能很多, 枚举左上角的时候就看不出对应右端点总和 $n^2$ 这个均摊.
B. 异或
给定序列 $a_n$, $q$ 次询问全局异或上 $x$ 后的逆序对个数.
$n, m\le 10^5$
感觉有一点点像南外题的 NOIP模拟赛44 逆序对
因为异或你肯定想拆位才能做, 才能看大小关系, 那么可以把每个数的二进制表示看成一个字符串, 大小关系就成了字典序, 而异或就是翻转某些位上的大小关系(让第 $i$ 位 $0>1$), 于是一种计算逆序对的方式是, 计算前 $i$ 位相同的数中, 当前位为 $1$ 的对当前位为 $0$ 的贡献, 这个前 $i$ 位相同很01trie, 于是建出01trie, 把每个数的下标插入到叶子上, 从下往上归并排序就能统计出某个节点的左右儿子之间的逆序对, 发现翻转某一位大小关系只是把一层的贡献从左对右换成右对左, 于是就做完了.
C. Essence of Twilight
LOJ Round6 花火
D. 数表
求有多少个值域 $[0, 2^k)$ 的 $2\times n$ 矩阵满足同行同列数不相同, 且 $2n$ 个数的异或和为 $0$.
$n, k\le 10^6$
考虑每个数最多出现两次, 那么钦定出现两次的数有 $s$ 种, 剩下 $2n-2s$ 个数, 显然这 $s$ 种数的方案数是 $(V-(2n-2s))^{\underline s}$, 而剩下的数异或和仍 $0$ 且互不相同, 这个显然用容斥思想dp, $f_i=v^{\underline {i-1}}-(V-i+2)f_{i-2}$, 表示先选前 $i-1$ 个互不相同的, 若最后一个和前面的相同则把它们两个一起删掉会得到 $f_{i-2}$, 它们两个此时又有 $V-(i-2)$ 种选法.
于是接下来只要求一种方案安排这 $2s$ 个数使得它们没有两个在同一列.
todo
The 2nd Universal Cup. Stage 11: Nanjing
和zzk和mikefeng VP, 切2, 另外两人都切3, 被带飞了.
D看到slopetrick但不会写维护函数寄了.
D. Red Black Tree
红黑树要求每个点到任意后代叶子节点的路径上, 黑色点的
数量都相同. 称该性质为”红黑树性质”.
现在给定一棵树, 每个点是红色或黑色, 对于所有 $k \in [1, n]$, 求为了让以节点 $k$ 为根的子树满足红黑树性质, 至少要修改几个点的颜色.$n\le 10^5$
我看你是烟火表演弱化版.
一眼dp设 $f_{u, x}$ 表示 $u$ 到子树内每个叶子经过 $x$ 个黑点的最小代价, 则 $f_{u, x}=\min_{i\in [0, 1]} (g(u, i)+\sum_{v\in son(u)}f_{v, x-i}$, 看到累加和 $min+$ 卷积的二维dp就上slopetrick.
于是两个操作分别是求和和对 $g$ 闵和, $g$ 要么是 $[0, 1]$ 要么是 $[1, 0]$, 都可以看成凸的.
那么对函数维护差分数组, 则分别是数组相加, 卷的时候要么是把差分数组的正数部分前面加一个 $1$, 要么是差分数组负数部分末尾加一个 $1$, 分差分为正数, 负数和 $0$ 段三段维护即可.