数数
数数题
会把计数相关问题放在这里.
一做数数发现现在已经不会做蓝题了.
1. Appleblue17
这一部分是appleblue17的cf和其他数数选做里的前几个.
CF1515E Phoenix and Computers
有 $n$ 台电脑排成一排, 每次可以手动打开一台没被打开的, 同时若一台电脑左右的电脑都被打开, 那么它会自动打开. 求把所有电脑打开的方案数. $n\le 400$
发现自动打开的电脑两边一定是手动打开的, 即它们不可能相邻, 所以其实是若干段手动打开的, 段段之间夹着一个自动打开的.
手动打开一个连续区间的方案数是 $2^{len-1}$ , 原因是我们每次只能像左边和右边拓展, 那么设第一个打开的是第 $k$ 个, 方案就是在剩下 $len-1$ 步中选 $k-1$ 步是向左拓展的, 所以方案数是
$$
\sum_{k=1}^{len} \binom{len-1}{k-1}=2^{n-1}
$$
那么把一个自动打开的和紧跟着的一段手动打开的作为一段, 设 $f_i$ 表示前 $i$ 个的方案, 则加上一个新段的方案数时除了乘上这一段的方案, 还要再在总步数里选若干步是新的这段的方案, 那么我们要知道总步数, 所以还要记录总步数或者之前分了几段, 增加一维, 设 $f_{i, j}$ 表示前 $i$ 个分了 $j$ 段, 转移就是
$$
f_{i, j}=f_{k-1, j-1}\times \binom {i-j+1}{i-k}\times 2^{i-k+1}\
f_{-1, 0}=1
$$
要把0当成一个自动开启的电脑留出来, 所以边界就成了-1, 实际实现可以所有下标一起加一
P6944/LOJ3405 [ICPC2018 WF]Gem Island
有 $n$ 个人每个人有一个宝石, 每天会随机一个宝石分裂成两个, 求 $d$ 天后拥有宝石前 $r$ 多的人所拥有的宝石数之和的期望, 不膜. $n, d\le 500$
设序列 $A$ , $a_i$ 表示 $d$ 天后第 $i$ 个人拥有的宝石数, 试着算算它出现的概率.
$$
\begin{aligned}
\text{A的方案数}&=\dfrac {d! }{\prod_i (a_i-1)! }\times \prod(a_i-1)! \
&=d!
\end{aligned}
$$
解释一下这个式子:
乘号左边的部分是我们确定下来每一天是给哪个人加的, 这个过程相当于对于一个天数构成的排列对一个排列我们让前 $1-a_1$ 个给第一个人, 接下来 $a_2$ 个给第二个人. . . 再除掉这么每一组分组后组内相对顺序.
乘号右边的部分是把每天由谁得这个关于人的方案数再变成关于宝石的方案数, 考虑一个人第 $i$ 次收获宝石的方案数是 $i-1$ , 那么这个人 $i$ 得到宝石的方案数就是 $(a_i-1)!$ 再乘起来.
于是发现每个 $A$ 的概率是相同的, 那么接下来就是算对于所有的 $A$ 它们的前 $r$ 大之和, 先考虑如何求 $A$ 的方案数, 此时可以先减去每个人一开始有的那个宝石方便计算:
这时有一种十分奇妙的状态设计, 考虑由于我们不关心 $a_i$ 的顺序, 所以我们假定它是递减的, 我们把宝石排成一个矩阵, 第 $i$ 列表示第 $i$ 个人的情况, 像这个样:
1 | **** |
这个图对应的 $A$ 是 $6, 6, 6, 6, 5, 5, 4, 4, 4, 2, 2$
横着关于人递推是困难的, 于是把它竖着递推, 由于此时向上递推时更高的顶大小一定小于更低的所以我们要知道顶的大小, 由于最后要求 $\sum a_i=d$ 所以要记录和, 于是设 $f_{i, j}$ 表示一共有 $j$ 个宝石, 其中有顶有 $i$ 个的方案数, 那么转移就是枚举上一层的大小, 即
$$
\begin{aligned}
f_{i, j}&=\sum f_{k, j-i}\times\binom{k}{i}\
f_{n, 0}&=1
\end{aligned}
$$
可以类比这个列出和的, 设顶大小为 $i$ , 共 $j$ 个的所有情况前 $r$ 大和的和为 $g_{i, j}$ , 则有转移:
$$
\begin{aligned}
g_{i, j}&=\sum (g_{k, j-k}+f_{k, j-k}*min(r, i))*\binom{k}{i}\
g_{n, 0}&=0
\end{aligned}
$$
然后dp就行了, 这个题不膜, 要直接带着long double从头算到尾.
CF1630E Expected Components
收录到polya定理初学中
ARC132E Paw
给定字符串 $s$ 包含 $\texttt{< > . }$ 三种, 表示向左的足迹, 向右的足迹和洞. 你每次会随机一个洞钻出来, 把洞填平, 然后随机左右两个方向走到下一个洞或走出字符串, 并把沿途所有位置都覆盖为你走的方向的足迹(沿途不包括你停止的那个洞). 直到没有洞. 求最后局面向左足迹的期望个数.
$\vert s\vert \le 10^5$
这种题要考虑形成局面的性质.
发现我们最后的局面一定是 $\texttt{<<\ldots<<. ==\ldots==. >>\ldots>>}$ , 且 $\texttt{=}$ 两边两个洞中间没有洞, 这里 $=$ 表示未走过的地方. 因为考虑不会出现 $\texttt{>><<}$ 的情况是因为停止需要一个洞, 而由这个洞出发的时候要么覆盖顺延右边的 $\texttt{<}$ 的要么顺延左边的, 一定会把这个局面填掉. 不会出现 $\texttt{<<>>}$ 因为这个点在出发一个之后就没了不能出发一个相反的, 所以局面只能是相邻两个洞向外发出的足迹.
那么枚举相邻两个洞, 考虑形成这个局面的概率, 发现左右是独立的, 以向右部分为例, 若 $f_i$ 表示向右形成前 $i$ 个的全局概率(所有方案中右边是对的的概率), 则有 $f_i=f_{i-1}\times (1-\dfrac{1}{2n})$ , 意思是只有选到 $i$ 这个位置并且向左走不行. 发现直接把左右两边对应概率乘起来即可因为两边都是全局的概率且互不影响.
CF1621G Weighted Increasing Subsequences
给定 $a_n$ , 对于 $a$ 的所有上升子序列 $a_{i_1}\ldots a_{i_k}$ , 其权值为 $a_{i_j}<a_x\And x>k$ 的 $j$ 个数, 对所有上升子序列求和.
$n\le 2\times 10^5$
钦定每个上升子序列 $a_{i_1}\ldots a_{i_k}$ 被最后一个大于a_{i_k}的 $x$ 贡献.
于是枚举 $x$ , 考虑计算贡献.
那么 $a_x$ 与 $a_j$ 行成的贡献是在 $[1, x)$ 中的上升子序列个数(这里是于拆贡献成 $x$ 与上升子序列中每一个小于它的数对的个数).
这个就是以 $i$ 结尾的, 乘上以 $i$ 开头但没有接到 $x$ 的个数. 因为 $x$ 是最后一个大于 $a_k$ 的, 所以没有接到 $x$ 后面的子序列, 于是后面这个等于以 $i$ 开头的个数减去以 $i$ 开头, $x$ 结尾的个数.
考虑直接把这些数都拿出来跑一遍dp, 那么这两个都可以1log算. 注意到设 $y$ 为大于 $x$ 的最大的 $y$ , 则 $a_x\in [a_y, a_z)$ , 并且 $y$ 恰好是下一个 $x$ ( $x$ 就是后缀 $\max$ , $y$ 恰好是下一个后缀 $\max$ ), 所以每个 $x$ 只会被拿出来算一遍. 就结束了.
[think] 钦点的东西可能也需要枚举, 第一个, 最后一个, 最大的这样的.
XXI OpenCup Grand Prix of SPb J Justice For Everyone
给定 ${a_n}$, 每次可以选定 $i\ne j$ 使得 $a_i: = a_i+1, a_j: = a_j+1$, 求有多少种方式最后得到 ${b_n}$, 且过程中 $\forall p\ne q, a_p\ne a_q$
$n\le 30, a_i, b_i\le 200$
好厉害的题.
首先考虑如果没有限制, 那么设 $d_i=b_i-a_i, s=\dfrac{1}{2}\sum d_i$, 设出 $n$ 元生成函数, 答案可以写成
$$
\begin{gathered}
Ans=[x_i^{d_i}]\ (\sum_{i, j}x_ix_j)^{s}\
=[x_i^{d_i}]\dfrac{1}{2^s}((\sum x_i)^2-(\sum x_i^2))^{s} \
=2^{-s}[x_i^{d_i}]\sum_j\binom{s}{j}(-1)^j(\sum x_i)^{2s-2j}(\sum x_i^2)^{j}\
=2^{-s}\sum_j\binom{s}{j}(-1)^j\sum_{\sum_k e_k=j} \binom{2s-2j}{d_1-2e_1, d_2-2e_2\ldots d_n-2e_n}\binom{j}{e_1, e_2\ldots e_n}\
\because \binom{n}{a_1, a_2\ldots a_n}=\dfrac{n! }{\prod (a_i! )(n-\sum a_i)! }\
\therefore ANS=2^{-s}\sum_j\binom{s}{j}(-1)^j\sum_{\sum_k e_k=j} \dfrac{(2s-2j)! j! }{\prod_i(e_i! (d_i-2e_i)! )}\
let\ F_d(z)=\sum_{2j<d}\dfrac{z^j}{j! (d-2j)! }\
\therefore ANS=2^{-s}\sum_j\binom{s}{j}(-1)^j\sum_{\sum_k e_k=j} (2s-2j)! j! [z^j]\prod F_{d_i}(z)\
let A(j)=2^{-s}\binom{s}{j}(-1)^j\sum_{\sum_k e_k=j} (2s-2j)! j!
\end{gathered}
$$
这是没有限制的情况, 当有限制的时候, 考虑若存在两个位置相同, 则以后可以把它们的值互换, 最后终点互换, 所以存在相两个数在某时刻相同的方案构成双射, 类似LGV引理求互不相交路径的证明, 发现答案可以是 $\sum_ (-1)^pH(a_i\to b_{p_i})$, 而这个就是 $\sum_(-1)^p\sum_j A(j)[z^j] \prod_i F_{b_{p_i}-a_i}(z)$, 这里可以把 $A$ 和提取系数提到最外面, 里面就是若干多项式构成的矩阵的行列式的形式, 于是设矩阵 $M, M_{i, j}=F_{b_j-a_i}(z)$, 求行列式提取系数再带入刚才 $Ans$ 中的部分就是答案了.
然后直接乘多项式可能不很好, 不如先用点值算再插回来.
PtzWinter2022 Day3 C Inversions
求所有长 $n$ 的排列的逆序对数的 $k$ 次方之和, $n\le 10^{18}, k\le 1000$
组合意义可以认为是排列中的所有逆序对选出 $k$ 对可以重的方案数, 或者说选出 $k$ 对位置每对都是逆序对的方案数之和, 那么可以看出答案是 $2k$ 次多项式.
有 $k$ 个逆序对的排列生成函数怎么写? 设 $F_t(x)=\sum_{i=0}^t x^i$, 那么 $k$ 个逆序对的方案数是 $g_k=[x^k]G(x), G(x)=\prod_{i=0}^{n-1}F_t(x)$, 而题目要求 $\sum_{i}i^kg_i$, 遇到高次常见方法转下降幂
$$
\begin{gathered}
Ans=\sum_{i}i^kg_i\
=\sum_{i}\sum_j i^{\underline{j}}{k\brace j}g_i\
=\sum_{j=0}^k {k\brace j}\sum_i g_ii^{\underline j}
=\sum_{j=0}^k {k\brace j}\sum_i G^{(j)}(1)
\end{gathered}
$$
$G=\prod F$, 考虑 $F_t^{(j)}(1)=\sum_{i=0}^{t} i^{\underline j}=\dfrac{t^{\underline{j+1}}}{j+1}$, 而 $(AB)^{(n)}=\sum_{i=0}^n \binom{n}{i}A^{(i)}B^{(n-i)}$, 对应了EGF的卷积, 所以把 $F_t(j)(1)$ 的值写成EGF卷起来即可, 复杂度 $k^2\log k$
[trick] 普通幂转下降幂之后的累加形式可以用求导带值简化.
CF1641E Special Positions
给定长度为 $n$ 的数组 $a$, 长度为 $m$ 的数组 $p$, 其中 $1 \le p_i \le n$ , 而且 $\forall j, p_i \not = p_j$.
在 $p$ 中等概率选定一个非空集合, 求 $\sum_{i = 1} ^ n a_i \times \vert i - p_j\vert$ 期望 其中 $p_j$ 是选定集合中 $\vert i - p_j\vert$ 最小的 $p$.
$m \le n \le 10^5, a_i \le 998244352, 1 \le p_i \le n, p_i$ 两两不同.
期望线性性, 考虑 $a_i\vert i-j\vert$ 的概率, 考虑 $i<j$ 情况, 那么设 $s_i$ 表示小于 $i$ 的 $p$ 的个数, $b_i$ 表示 $i$ 是否是 $p$ 中的数, 则概率是 $2^{-(s_{j}-s_{2i-j})}a_ib_j(j-i)$, 设 $v_i=2^{s_i}$, 变成 $j\dfrac{v_{2i-j}}{v_{s_j}}a_ib_t-i\dfrac{v_{2i-j}}{v_{s_j}}a_ib_t$ 两边各自可以看出卷积的形式, 然后因为有 $i<j$ 的限制所有分治NTT即可.
P8114 [Cnoi2021]六边形战士
求边长为 $a, b, c$ 的六边形平面图二分图完美匹配数量.
$a, b, c\le 10^6$
是个很经典的题, 把所有非匹配边割断会把匹配边分开:
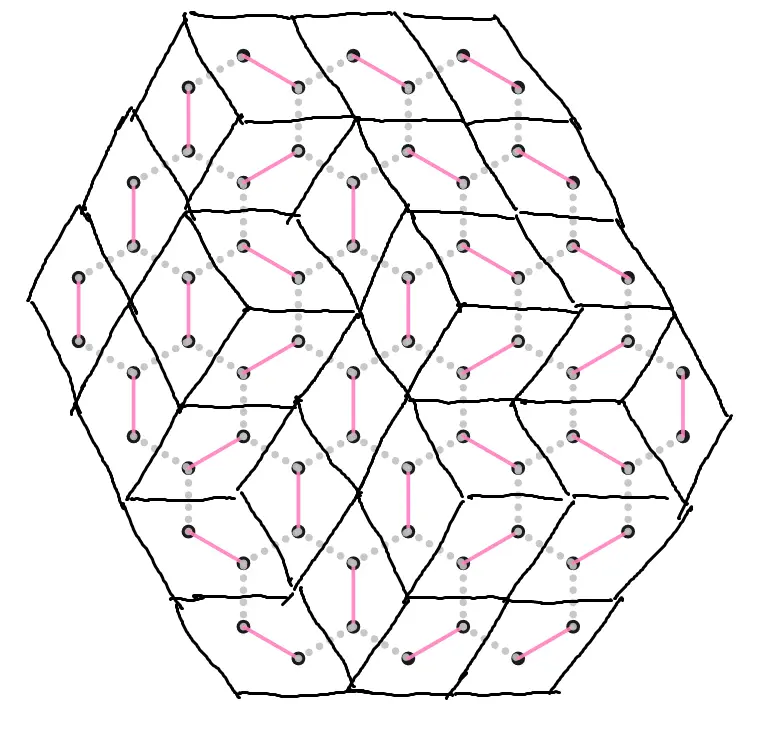
然后瞪大眼睛瞪出3d感, 发现一个匹配和一个立方体堆叠双射, 则只要求长 $a$ 宽 $b$ 高 $c$ 的长方体内的堆叠数, 要求所有面都能漏出来, 然后观察一列立方体最高的轮廓形成的轨迹, 可以对应成从 $1, 1$ 出发每次向右或向下走走到 $(a+1, b+1)$ 的 $c$ 条路径, 且没有两条路径相互穿过的方案数, 那么把第 $i$ 条路径的起点终点都平移 $(i, i)$, 就成了互不相交路径, 就可以LGV引理了, 现在答案成了
$det(M), M_{i, j}=\binom{a+b}{a+i-j}$
然后它写成了一个巨大的矩阵化简/jk/jk/jk, 流程就是组合数的阶乘提出来, 然后凑成题目中的公式.
最后是线性的.
P4566 [CTSC2018] 青蕈领主
有一个长度为 $n$ 的排列 $a_n$, 给定对每个 $i$, 最大的 $l_i$ 使得 $[i-l_i+1, i]$ 是连续的, 定义连续为排序后是一段公差为 $1$ 的等差数列, 求可能的 $a$ 数量. $n\le 5\times 10^4$.
好强.
首先发现 $[i-l_i+1, i]$ 的区间一定不交, 否则一定可以更长, 那么区间包含关系可以形成树状结构, 对一个节点来说其子节点可以再看成一个单个的数去计数, 所以设点 $u$ 有 $son_u$ 个儿子, 答案就是 $\prod_u f_{son_u}$, 而 $f_n$ 表示 $n+1$ 个数构成排列且除了整个排列外没有长度大于 $1$ 的连续段, $f_0=0$.
那么 $f$ 是一个极小的定义, 考虑设其OGF为 $F(x)$, $G(x)=\sum_{i=1} i! x^i$ 为全排列, 根据刚才的分析, 考虑一个排列建出树之后根节点的分解, 大小为 $1$ 的排列分解不了, 就有了
$$
\begin{gathered}
G(x)=xF(G(x))+x\
F(G(x))=\frac{G(x)-x}{x}\
let\ H(G(x))=x\
\therefore F(x)=\frac{x}{H(x)}-1
\end{gathered}
$$
问题变为求 $H$, 因为不是只求一项所以拉反不好用了. 发现 $G$ 是微分有限的, 于是凑系数并带入 $H$:
$$
\begin{gathered}
G(x)=\sum_{i=1} i! x^i\
G’(x)=\sum_{i=1} i\cdot i! x^{i-1}\
(x-1)G(x)+x^2G’(x)+x=0\
(H(x)-1)x+H^2(x)G’(H(x))+H(x)=0\
\because G(H(x))=x\
\therefore G’(H(x))H’(x)=1\
\therefore (H(x)-1)x+\frac{H^2(x)}{H’(x)}+H(x)=0\
xH(x)H’(x)-xH’(x)+H^2(x)+H(x)H’(x)=0\
nh_n=\sum_{i=0}^{n-2}(i+1)h_{i+1}h_{n-1-i}+\sum_{i=1}^{n-1}h_ih_{n-i}+\sum_{i=0}^{n-1}(i+1)h_{i+1}h_{n-i}\
-g_1h_n=\sum_{i=1}^{n-1}(i+1)r_ir_{n-i}+\sum_{i=2}^{n-1}ir_ir_{n+1-i}\
\because F(G)=x
\therefore [x]F(G)=f_1g_1=g_1=[x]x=1
\end{gathered}
$$
卷积形式, 分治NTT, 复杂度 $n\log^2 n$.
[think] 对微分有限的东西求复合逆, 就微分列出微分方程, 再带入得到关于复合逆的微分方程, 再转递推式上FFT
补充一下, 写的时候会让人感到疑惑在于 $G, F, H$ 都是没常数的, 于是不能求逆, 但是你最后求的是 $\dfrac{x}{H}=\dfrac{1}{\frac{H}{x}}$ 就没问题了.
P8354 [SDOI/SXOI2022] 多边形
$n$ 条边的凸多边形每条边上又额外有 $a_i-1$ 个顶点, 求三角剖分数, 要求一条边上的两个顶点不能连线, 边中间上可以有顶点不连线.
$\sum a_i\le 5\times 10^5$
和普通的卡特兰数相比就是后面的两个限制.
对于一条边上可以有不连的只要选出点数就行了, 现在先假设所有点都要被选, 问题是同一条边的不能连线, 不容易发现若存在同一边连线必然存在恰好跨过一个点的边, 于是对这样的边容斥, 而钦点这样的相当于直接删掉中间的点.
终止假设, 于是对于删掉中间点, 删掉不选的点的最终局面的一条线段, 其贡献系数应该为 $1-(c-1)$($c$ 为跨过的段数), 其中第一个 $1$ 是正常贡献, 后面 $c-1$ 是枚举它跨过了中间的一个点. 设 $a_i$ 原题目多边形上一条边的段数, 则一条边上选 $k$ 条边的容斥系数最后就是
要对所有 $k$ 算这个东西, 也就是设
$$
F(x, z)=\dfrac{1}{1-z\frac{-2x^2+x}{(1-x)^2}}=\dfrac{(1-x)^2}{(2z+1)x-(z+2)x+1}
$$
有一个很粗暴的方法了, 求 $[x^{a_i}]F$, 看成关于 $x$ 的多项式, 就是线性递推那类的东西, 复杂度是 $T(n)=2T(n/2)+O(n)$, 则 $T(a_i)=a_i\log a_i$ 是可以过的, 然后对 $y$ 的多项式你应该带着点值算以卡常.
可以考虑拉反, 设 $G(x)=\dfrac{-2x^2+x}{(1-x)^2}$, $G(R)=x$, 则有
$$
[x^n]G^k=[x^{n-1}]\dfrac{1}{n}kx^{k-1}(\dfrac{x}{R})^n=\dfrac{k}{n}x^{n-k}^n
$$
我们把多项式的指数统一了! 现在只要知道 $(\dfrac{x}{R})^n$ 是啥, 设 $H=\dfrac{x}{R}$, 则因为
$$
G=\dfrac{-2x^2+x}{(1-x)^2}\
x=\dfrac{-2R^2+R}{(1-R)^2}
$$
$R$ 是微分有限的, 所以 $H=\dfrac{x}{R}$ 也是微分有限的, $H^n$ 也是微分有限的, 你可以得到一个线性的递推式.
[ARC132F] Takahashi The Strongest
小 $A, B, C$ 在玩石头剪刀布, 分别用 $R, S, P$ 表示. 小 $A$ 有 $n$ 个策略, 小 $B$ 有 $m$ 个策略, 一个策略是一个长度为 $k$ 的包含 $R, S, P$ 的字符串, 表示每一局会固定出什么. 对于小 $C$ 的一种策略, 如果在中途某一次小 $C$ 是绝对赢家, 那么小 $C$ 会开心. 对于小 $C$ 每种可能的策略, 求出有多少种 $A, B$ 的组合策略(一共有 $nm$ 种组合)使得小 $C$ 会开心.
- $1\leq k\leq 12, 1\leq n, m\leq 3^k$
即存在某一轮 $A, B$ 相同且恰好比 $C$ 少 $1$, 考虑定义 $4$ 进制类FWT的卷积使得对于每一位
$$
x\otimes y=\begin{cases}
x\ if\ x=y, \
3\ if\ x=y
\end{cases}
$$
用和FWT相同的方法构造矩阵, 即设 $j$ 对 $i$ 的贡献为 $c(i, j)$ 要求 $c(i, j)c(i, k)=c(i, j\otimes k)$, 则是要解 $c_i\in {-1, 1, 0}, c_3=c_0c_1=c_0c_2=c_1c_2$, 大概拿出来有 $[1, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 0], [1, 1, 1, 1]$ 的解(全 $0$ 没有逆), 有矩阵
$$
\begin{bmatrix}
1 & 0 & 0 & 1\
0 & 1 & 0 & 1\
0 & 0 & 1 & 1\
0 & 0 & 0 & 1
\end{bmatrix}
$$
实际上是做前缀和, 认为 $0, 1, 2\subset 3$. 显然有逆, 可以卷积. 求出 $A$, $B$ 策略卷起来的序列 $f_T$, 再把策略平移一位, 变成对每个 $S$(三进制)的 $\sum_{T\cap S\ne \varnothing}f_T$. 改成求 $\sum_{T\cup S=\varnothing}f_T$,
2. luogu某题单
然后做不动了appleblue太强悍. 随便找点, 下面是luogu上的一个题单
CF1657E Star Mst
求 $n$ 个点的无向完全图有多少个满足最小生成树的权值和等于所有和点1相连的边的权值和, 每条边边权为 $[1, v]$ , $n, v \le 250$
qyc场切
[trick] 这个条件首先等价于以1为根的菊花是它的最小生成树, 再考虑Kruskal的过程, 又等价于对于每个点, 1都是离它最近的点之一.
考虑对于一条 $u\to v, u, v\ne 1$ 的边, 在我们不知道 $1\to u$ 和 $1\to v$ 前是无法确定的, 所以要明确一个确定边权的顺序, 发现如果从小到大确定边权那么所有新的满足 $1\to u, 1\to v$ 已经确定的 $u\to v$ 的边权都只依赖于我们新加的边权而不依赖于旧的, 根据这个, 设 $f_{i, j}$ 表示加入了边权在 $[1, i]$ 的边, 一共有 $j$ 个连到 $1$ 上, 当转移时, 我们考虑新加入的这些边确定了哪些:
$$
f_{i, j}=f_{i-1, k}\times (v-i+1)^{\binom{j}{2}-\binom{k}{2}}\times \binom{j}{k}
$$
推转移式子的时候别忘了最后那个组合数.
注意指数上那个二项式系数不是对 $P$ 取模, 但其实也没事因为它们根本到不了要取模的大小.
然后你就做完了.
P5664 [CSP-S2019] Emiya 家今天的饭
给一个 $n$ 行 $m$ 列的矩阵 $A$ , 每个格子有个数表示选这个格子的方案数, 可以选任意多个格子, 要求每行只能选一个, 且若一共选了 $k$ 个数, 则不能有一列选超过 $\lfloor\dfrac{k}{2}\rfloor$ 个数. $n \le 100, m\le 1000$
这题首先看起来很dp, 发现这个每列个数不超过一半很难计算, 而又因为只可能有一列选的个数超过一半, 所以可以容斥, 枚举是哪一列超过了一半.
于是现在钦定第 $r$ 列超过一半计算方案数, 很容易想到设 $f_{i, j, k}$ 表示考虑这一列的前 $i$ 个数, 选了 $j$ 个第 $r$ 列的和其他 $k$ 个不在第 $r$ 列的. 这里记 $s_i=\sum_j A_{i, j}$ , 则转移为:
$$
f_{i, j, k}=f_{i-1, j-1, k}\times a_{r, i}+f_{i-1, j, k-1}\times (s_i-a_{r, i})
$$
但这样做算上枚举每一列的话复杂度是 $O(mn^3)$ 的, 无法通过, 发现我们之所以记录 $j$ 和 $k$ 是因为判断最后是否要这个值, 即是否在这一列里选了超过一半, 那么其实我们只要知道 $j-k$ 就行, 所以考虑设 $f_{i, j}$ 表示考虑这一列的前 $i$ 个数, 在这一列的比外面的多 $j$ 的方案数, 发现转移是简单的, 复杂度就成了 $O(mn^2)$
启发一种优化状态设计的方法.
P3214 [HNOI2011] 卡农
有 $m$ 个音, 要求选出无序的 $n$ 个互不相同的音的集合, 满足所有音都出现了偶数次. 对 $10^8+7$ 取模.
$n, m\le 10^6$
首先 $10^8+7$ 居然也是质数, 长见识.
首先这个的无序没有任何用处, 有序的除以 $n!$ 就行.
由于是偶数次, 让人想到异或, 所以转化为:
在 $[1, 2^m -1]$ 个数中选 $n$ 个互不相同的数满足异或和为0.
设选前 $i$ 个数的答案为 $f_i$ , 如果我们先随便放 $[1, i-1]$ , 最后在 $i$ 的位置放一个数 $x=a_1\mathrm{xor}a2. . . \mathrm{xor}a_{i-1}$ 就满足了条件, 这样的方案数是 $A^{i-1}_{2^m-1}$ 但却多算了以下两种情况:
$x=0$ , 说明前 $i-1$ 个已经异或起来是0了, 多算了 $f_{i-1}$ 个方案.
$x$ 在前面出现过, 那么把那个出现过的也删去, 剩下的还有 $f_{i-2}$ 个方案, 此时 $x$ 有 $2^m-1 -(i-2)$ 种可能(与前面的其他数互不相同), 同时与其相同的那个数的下标有 $i-1$ 种, 一共多算了 $(2^m-1-(i-2))(i-1)f_{i-2}$ 个方案.
最后注意
$$
A^k_n\bmod P=A^k_{n\bmod P} \bmod P
$$
可以简单归纳法证明.
P2606 [ZJOI2010]排列计数
求有多少个长为 $n$ 的排列满足 $p_{i}>p_{\frac{i}{2}}$ . $n \le 10^6$
容易想到若 $i$ 向 $\dfrac{i}{2}$ 连边会得到一棵完全二叉树, 而此时根一定是当前最小值, 左右子树则是互不干扰的, 形成一个递归结构, 于是我们考虑dp.
设 $f_i$ 表示长度为 $i$ 的排列的答案, 也就是节点数为 $i$ 的树的答案, 同时设 $lson_i, rson_i$ 表示它左右子树的大小, 则有:
$$
f_{i}=\binom i {lson_i}\times f_{lson_i}\times f_{rson_i}
$$
然后做完了.
P6453 SP3734 PERIODNI - Periodni
给定一个 $n$ 列直方图(底部对齐的若干矩形)网格, 每列高度各不相同, 现在要在其中摆放 $k$ 个车, 要求车相互无法攻击. 求摆放方案数.
$n, k\le 500$ .
看到这个直方图想到给定直方图求最大矩形那个题的笛卡尔树做法, 我们把笛卡尔树建出来dp, 考虑以序列下标为二叉查找树的关键字, 以矩形高度建小根笛卡尔树, 因为每一列高度各不相同所以, 所以相当于把直方图横向分隔成若干层, 如图:
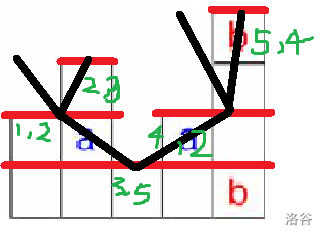
那么接下来只要考虑如何在这棵树上dp, 容易想到设 $f_{u, i}$ 表示 $u$ 的子树内放了 $i$ 个车的方案数, 若 $v$ 为 $u$ 的儿子, 发现仅仅在自己这里选择 $j$ 个的方案数就是 $\binom{w}{j}\binom{h}{j}j!$ , 然后按这个转移即可.
P3244 [HNOI2015]落忆枫音
给定 $n$ 个点 $m$ 条边的DAG, 在此基础上再添加一条 $x\to y$ 的边, 求此时以1为根的不同的生成树个数. $n\le 10^5$
在DAG上这个东西时好求的, 只要把每个点的入度乘起来即可, 意思是给每个点选一个父亲. 但现在又多了一条边, 可能形成至多一个环, 那么只要减去恰好选了这个环的方案, 相当于我们只确定了环上点的父亲, 所以方案数就是不在环上的所有点的入度的乘积, 两者相减即可.
P6672 [清华集训2016] 你的生命已如风中残烛
$m$ 张牌的牌堆,牌是区分的, 同时 $n$ 张牌还有属性 $w$ 表示可以打出后能再摸几张, 求有多少种牌堆的排列使得你一轮可以把所有牌都摸没. 保证 $\sum w=m$ .
首先可以把没有属性 $w$ 的牌看成 $w=0$ .
考虑摸没的条件, 摸完前 $k$ 张牌的手牌数为 $1+\sum_{i=1}^k w_i - k$ , 所以要求对于任意 $k$ 这个式子为正, 于是可以给每个 $w_i$ 先减去1. 变成保证 $\sum_i w_i=0$ , 要求所有前缀和都非负的个数.
有一个Raney引理: 对任意和为1的整数排列, 其所有循环平移形成的排列中, 有且仅有一个满足任意前缀和为正.
这个证明很简单, 看成折线图后就是只有从折线图的最低点出发的情况满足条件. 如果有多个相同的最低点则只能选最后一个, 所以只有一个出发点满足条件.
但这个问题没有和圆排列的直接一一对应的关系, 原因是当出现多个最低点时可以选择任意一个.
可能会想到在开头处添加一个1转化过去, 会发现我们在原始问题上添加1可能导致去掉这个1后两种方案本质相同. 因为第一个位置的数不一定是1.
但如果在最后添加一个-1就没有问题, 因为假设仍有多个最低点只能选第一个, 否则我们会跨过这个-1来到第一个最低点, 那么第一个最低点的位置就会比当前的更低. 于是我们又建立起了一一对应的关系.
接下来计算答案就简单了. 要注意这里 $w$ 相等的卡牌是区分的, 所以不用Polya而可以直接圆排列计数, $m+1$ 个卡牌的圆排列一共有 $\dfrac{(m+1)! }{m+1}=m!$ 个, 同时由于我们添加的-1和其他-1是不区分的, 所以除掉-1个数 $m-n+1$ , 答案为 $\dfrac{m! }{m-n+1}$ .
3. CF板刷
CF选择标签combination板刷
CF1730E Maximums and Minimums
给定序列 $a$ , 求区间中最大值是最小值的倍数的区间个数.
$n\le 5\times 10^5, a_i\le 10^6$
$10^6$ 以内因数个数不到300. 于是算法复杂度有可能是 $nd$ 的. (不然应该出到 $10^9$ )吧.
枚举最大值和对应因数, 我们能做到 $nd\log n$ . 这个部分还很套路: 就是考虑能做最大值的区间, 对应最小值能做最小值的区间. . . $\log n$ 出现在对于每一个最大值找出左边/右边第一个最小值的位置.
但是问题是, 怎么去 $\log n$ 呢? 好, 打开jiangly代码,lower_bound, 嗯, 结束了. 原来是 $nd\log n$ .
哦去 $\log$ 是简单的, 考虑我们相当于 $nd$ 次询问一个数左边等于另一个数的位置. 那么假设最大值枚举的时候从左往右, 就只需要对于每一个值维护它最后一次的位置即可.
另一个做法是分治, 扫左端点得到左边最大最小, 那么钦定左边贡献最大, 然后枚举约数好像复杂度一样.
CF1728G Illumination
给定一条长 $d$ 数轴上的 $n$ 个灯和 $m$ 个点的位置序列 $l, p$ , 灯 $i$ 可以照亮 $[l_i-w_i, l_i+w_i]$ 范围内的点, 其中 $w_i$ 是 $[0, d]$ 的整数.
$q$ 次询问, 每次询问在已有 $n$ 个灯的基础上添加一个新灯后 $w$ 的方案数使得每一个点都能被照亮.
$n\le 2\times 10^5, m\le 16, q\le 5\times 10^5, d\le 3\times 10^5$ .
先考虑一次询问怎么做, 能dp吗?
$f_{i, j}$ 表示前 $i$ 个灯照亮前 $j$ 个点, 发现可以转移. 那么直接转移写成矩阵, 预处理前缀积和后缀积就行了. 复杂度是 $nm^3+qm^3$
另一个做法是考虑容斥, 枚举点集 $S$ , 确定它们都被覆盖是困难的, 但要求 $S$ 内的点都不被覆盖只要让相邻两个属于 $S$ 的点之间的灯照不到这两个端点即可. 相当于直接限制每个灯的最大值. 那么预处理数组 $f_{l, r}$ 表示 $[l, r]$ 中的灯照不到点 $l$ 和 $r$ 即可.
现在有了多组询问, 枚举新加的点照亮的范围, 并预处理照亮这个范围外的点的方案. 注意范围外的点这一点集一定是前缀和后缀, 所以点集只有 $m^2$ 个.
CF1671F Permutation Counting
求逆序对数为 $k$ , 下降数为 $x$ 的长 $n$ 的排列数量.
$n\le 998244352, k, x\le 11$
下降数是 $\sum [a_i>a_{i+1}]$
牛逼题.
观察性质拆贡献, 把满足 $i<\max_{j\le i} a_j$ 的连续的一段称为一段, 那么发现段间没有贡献.
对于每一段, 考虑其内部排列, 一段长度最多是 $12$ 否则逆序对数就会超过 $11$ , 于是就先考虑内部排列, 设 $f_{s, j, k}$ 表示 $s$ 集合已经选了, 有 $j$ 个逆序对, $k$ 个下降的一段的个数, 枚举下一个填几即可转移. 就能 $2^12\times 11^2\times 12$ 的dp它了.
接下来考虑, 一个长度是 $2$ 的段会产生 $1$ 个逆序对, 所以我们最多拼 $11$ 个段, 于是设 $g_{i, j, k, l}$ 表示拼了 $i$ 个段, 这 $i$ 个段一共 $j$ 个数, 有 $k$ 个逆序对, $l$ 个下降的方案数, 转移是类似背包的dp.
最后算答案的时候, 我们累加所有 $k, l$ 是题目要求的那些状态值, 那么对于除了这些长为 $2$ 的段之外的那些长为1的段, 每一个数都是唯一确定的, 于是直接用隔板法再乘一个组合数即可.
很厉害啊
更好想的感觉是另一个: 猜测固定 $i, j$ 后答案是关于 $n$ 的, 次数不超过 $11$ 的多项式, dp打出 $11\times 11\times 11$ 的表, 然后拉格朗日差值.
CF383E Vowels
给出 $n$ 个长度为 $3$ 的由 $\texttt{a}\ldots\texttt{z}$ 组成的单词, 一个单词是正确的当且仅当其包含至少一个元音字母. 这里的元音字母是 $\texttt{a}\ldots\texttt{x}$ 的一个子集. 对于所有元音字母集合, 求这 $n$ 个单词中正确单词的数量平方的异或和.
$n\le 10^4$
一个单词是错误的当且仅当这个单词与元音字母集合不交, 等价于它的补集是元音字母集合超集, 于是补集之后做超集和就能得到数量.
但问题是这样是 $10^7$ 的, 且没有利用单词长度为3的特性.
看题解, “注意到4s, 所以 $O({\vert\sigma\vert}2^{\vert\sigma\vert})$ 完全能过. “这样啊.
CF1603F October 18, 2017
给出 $n, k, x$ , 求长 $n$ , 每一项在 $[0, 2^k)$ , 且任意子序列异或和不为 $x$ 的序列个数. $n\le 10^9, k\le 10^7, \sum k\le 5\times 10^7, x< 2^20$
$x=0$ 是特殊的, 其他是相同的.
当 $x=0$ 时, 相当于选出若干个线性无关向量. 方案数为 $\prod 2^k-2^{i}$ , 就是每一次选前面不能表示的. 复杂度 $O(k)$
当 $x\ne 0$ 时, 每个数的情况相同, 所以求对于一个序列其能表示的数的个数求和后再除以数的总数就是答案. 而一个数列能表示的数的个数就是, 若把这个数列中所有数视作向量弄成一个矩阵后矩阵的秩为 $r$ , 个数就是 $2^r$ . 于是只要求长 $n$ 的序列秩为 $1\ldots n$ 的分别是多少即可.
考虑dp这个东西, 设 $f_{i, r}$ 表示前 $i$ 行, 秩为 $r$ 的方案数. 有
$$
f_{i, r}=f_{i-1, r}\times 2^{r}+f_{i-1, r-1}\times (2^k-2^{r-1})
$$
复杂度 $nk$
用生成函数求, 写成生成函数, 我们可以先选出一组基, 方案数是 $\prod_i (2^k-2^i)$ , 然后再把其他的数添加进去, 第 $i$ 个数后添加方案数是 $2^i$ . 后面这个生成函数是
$$
\prod \dfrac{1}{1-2^ix}
$$
而
$$
\dfrac{1}{\prod ^n_{i=0}(1-q^ix)}=\sum_{i>=0}x^i{i+n\brack n}_q
$$
所以后面这个生成函数 $n-r$ 项系数就是 ${n\brack n-r}_q$
于是就做完了.
qanalogy=不可做
CF1295F Good Contest
求长 $n$ 序列 $a$ 单调不增的概率, 其中 $a_i$ 在 $[l_i, r_i]$ 中等概率随机.
$n\le 50, l_i, r_i\le 998244353$
$f_{i, j}$ 表示前 $i$ 个单调不增以 $j$ 结尾的方案数, 则
$$
f_{i, j}=(\sum_{k\ge j} f_{i-1, k})
$$
但值域很大, 会寄.
$f_i$ 是 $f_{i-1}$ 做后缀和再截取一个区间, 有什么好办法?
离散化成若干值域区间! 变成 $a_i$ 在第 $j$ 个值域区间, 那么此时转移要考虑一个区间内转移到当前区间内的情况, 发现根本不会做.
考虑不枚举 $j$ 转而枚举 $i$ , 即从 $f_{k}{j+1}$ 转移过来, 这样只要算从最后一段里选一个不降的序列即可. 而从长 $l$ 的值域段选长 $a$ 的不降序列只要组合数 $\binom {l+a-1}{a-1}$ 即可.
另一个方法, 容易想到直接维护分段函数, 那么需要对分段函数求前缀和, 是容易的.
CF1523E Crypto Lights
有 $n$ 个台灯初始时都是暗的, 每次等概率随机一个暗台灯将其点亮, 若点亮后存在一个长度为 $k$ 的连续段有大于一个台灯被点亮则立刻停止, 求期望点亮多少台灯. 答案对 $10^9+7$ 取模.
$n, k\le 12^5$
考虑算开启 $i$ 个后能继续的概率.
那么这个就是从这 $n$ 个灯中选 $i$ 个灯相隔 $k$ 以上的概率. 这个考虑选 $i$ 个相隔 $k$ 以上的灯可以看作选 $i$ 个灯亮, 再在其中插入剩下的灯. 那么方案数就是 $\binom {n-i+(i-1)(k-1)+i}{i}\times i!$ . 就结束了.
CF1495D BFS Trees
给定一张图, 以 $s$ 为根的生成树是厉害的指 $s$ 到任意一点的树上距离等于实际距离. 求有多少个生成树同时是以 $x$ 为根厉害的也是以 $y$ 为根厉害的. 对所有 $(x, y)$ 求答案.
$n\le 400, m\le 600$
考虑如果 $x\to y$ 有两条及以上最短路, 那么一定不行.
找到这一条后, 这一条链一定原封不动照搬到这棵树上. 对于剩下的点, $u$ 的父亲可以为 $f$ 当且仅当 $dis(u, x)=dis(x, f)+1, dis(u, y)=dis(y, f)+1$ .
然后统计每个点可以的父亲个数, 直接乘起来就结束了.
CF1264D Beautiful Bracket Sequence
给定一个含 $\texttt{? }$ 的括号序列. 定义一个括号序列的权值为删除一些字符使其成为合法的匹配括号串后, 括号匹配的最深深度. 求把 $\texttt{? }$ 替换成括号的所有方案中, 括号序列的权值之和.
Version1
$n\le 2000$
[trick] 一个括号序列有唯一的位置使得左边的左括号个数等于右边的右括号个数.
这个位置显然就是最大的匹配位置, 于是可以枚举深度最大的匹配之间的空隙(如果有多个, 算在第一个空隙). 设左边有 $l$ 个左括号, 右边有 $r$ 个右括号, 左边有 $x$ 个问号, 右边有 $y$ 个. 那么方案数就是
$$
\sum_{i=0}^{x} (l+i)\times \binom xi \binom {y}{l+i-r}
$$
含义是枚举左边有多少个问号是左括号, 那么 $l+i$ 是深度, $\binom xi$ 是从左边挑出 $i$ 个, $l+i-r$ 是右边需要这么多括号定为右括号. 是我们钦定它是第一个深度最大的空隙并且右边确定了对应数量的右括号, 所以左边所有左括号都是可以贡献给这个空隙的. 所以这是正确的. 复杂度 $O(n^2)$
Version2
$n\le 10^6$
考虑化简这个式子:
$$
\begin{aligned}
& \sum_{i=0}^{x} (l+i)\times \binom xi \binom {y}{l+i-r}\
=& l\sum_{i=0}^{x} \binom xi \binom {y}{l+i-r} +
\sum_{i=0}^{x} i\binom xi \binom {y}{l+i-r}\
=& l\sum_{i=0}^{x} \binom xi \binom {y}{l+i-r} +
x\sum_{i=0}^{x} \binom {x-1}{i-1} \binom {y}{l+i-r}\
=& l\sum_{i=0}^{x} \binom {x}{x-i}\binom {y}{l+i-r}+x\sum_{i=0}^{x} \binom{x-1}{x-i}\binom {y}{l+i-r}\
=&l\binom{x+y}{x+l-r}+x\binom{x+y-1}{x+l-r}
\end{aligned}
$$
拿这个做即可.
第二部分知道范德蒙德卷积应该是简单的. 主要是第一部分枚举一个关键(最大值)的位置后计算组合数这个方法比较巧妙.
CF1437F Emotional Fishermen
给定长 $n$ 的序列 $a$ , 求 $a$ 重新排列后, 对于每一个位置 $a_i$ 和 $x=\max_{j\in[1, i-1]} a_j$ , 满足 $x\ge 2a_i$ 或 $a_i\ge 2x$
膜998244353. $n\le 5000$
考虑用 $a_i\ge 2x$ 的把序列分成若干段, 每一个段内 $2a_i\le x$ , 每一个数可以作为划分点, 或放在第一个大于自己二倍的划分点之后. 排序后用这个dp. 设 $f_i$ 表示最大值是 $a_i$ 的方案数(加入小于 $\dfrac{a_i}{2}$ 的所有数), 此时排列中被加入的数目设为 $len_i$ .
$$
f_i=\sum f_j \times A^{len_i-len_j-1}_{n-len_j-2}
$$
$f_i$ 位置是 $a_j$ 后第一个没被放的位置(否则空出来一个位置没有东西可以放), 它的位置是确定的. 而在值域 $(\dfrac{a_j}{2}, \dfrac{a_i}{2}]$ 中的这些数可以再这一次被加入. 并且可以在自己后面任意放(不能在前面, 前面已经没空位了). 于是就是这个样子了. 复杂度 $n^2$ .
仍然是费用提前计算的思想(不过把费用改成方案数). 我们应该有意识枚举所有可能都状态设法和转移方向. 并且dp排列的时候由于其每个值只能出现一次基本都是从值域入手把值域分成若干段去计算.
CF1237F Balanced Domino Placements
给定一个 $n\times m$ 的棋盘, 上面放了 $k$ 个 $1\times 2$ 的骨牌, 要再任意放骨牌, 要求同一行, 同一列只有最多有一个骨牌, 求方案数.
$n, m\le 3600, k\le 2400$
行和列是隐晦的独立的.
看起来似乎行和列会互相影响. 但实际上可以看作, 若选择 $x$ 个横放和 $y$ 个竖放, 就是要选择 $x+2y$ 行, 其中有 $y$ 对两两相邻. 对列也一样. 那么确定这个选择的方案之后剩下就是两两配对了. 所以预处理 $f_{x, y}, g_{x, y}$ 分别表示在确定横竖个数之后选行列的方案数, 答案就是
$$
\sum f_{x, y}g_{x, y}x! y!
$$
注意这里不是 $(x+y)!$ , 因为 $2y$ 个相邻行和只能和 $y$ 列匹配, $2x$ 个相邻列和 $x$ 行匹配, 两组匹配是独立的.
最后就是处理 $f, g$ 的问题了. 以 $f$ 为例, 对于每一个能选的行当连续段且确定 $x, y$ 后方案数很好确定. 那么这么背包上去只能做到三次方.
我们不需要同时考虑 $x$ 和 $y$ , 可以先确定选 $y$ 个行对当方案数, 再在剩下的里面选单独行是直接组合数. 而第一个就dp就好了. 前 $i$ 行选 $j$ 对的方案这样的. 就做完了.
dwt钦定是简单题

CF1185G Playlist for Polycarp
有 $n$ 首歌, 每一首长 $t_i$ , 类型为 $g_i$ , 求选择一些歌并排列的方案使得任意两个相邻 $g_i$ 不同且总时长恰好为 $T$ .
$g_i\le 3$
Version1
$n\le 15, T\le 225, t_i\le 15$
直接状压dp. $f_{s, i}$ 表示 $s$ 已经被选了, 最后一个选的第 $i$ 首.
Version2
$n\le 50, T\le 2500, t_i\le 50$
不能直接状压dp了, 需要组合数学靠运气.
我们可以直接处理满足编号限制的dp: $f_{i, j, k, 0/1/2}$ 表示 $i$ 个第一种, $j$ 个第二种, $k$ 个第三种, 最后一个是哪一种的方案数. 暴力转移.
那么接下来就要考虑一个合法集合使得满足时间限制. 看看数据很小可以直接枚举 $i, j, k$ , 那么就要知道此时等于时间的方案数. 这是一个subset sum, 不过有三个集合. 所以就使劲背包就好了.
CF1558D Top-Notch Insertions
对于一个长度为 $n$ 的序列 $a$ 做插入排序, 即依次考虑 $a_2, \cdots, a_n$ 每个元素:
如果 $a_i \ge a_{i - 1}$ , 即前缀依然保持不下降, 不做操作.
否则, 找到最靠前的位置 $p$ , 使得 $a_i < a_p$ , 然后将 $a_i$ 插入到 $a_p$ 前面, 并重新标号序列. 记这次插入为 $(i, p)$ .
接下来给定 $m$ 个二元组 $(x_i, y_i)$ , 求有多少个长度为 $n$ 的序列 $a$ , 满足 $\forall i, a_i \in [1, n] \cap \mathbb N$ 且做插入排序恰好按照给出的元组进行给定的 $m$ 次插入.
输出序列的数量对 $998244353$ 取模的结果.
根据若干个插入条件, 可以唯一确定原序列相对顺序. (就是这些插入相当于对原序列做了一个置换重排, 根据这个可以获得 $a$ 的排序.
但此时拿到的 $a$ 并不是一个不降的要求(我们会得到若干 $>$ 和若干 $\ge$ 串起来的关系), (可以理解一下这个关系蕴含了能获得的全部信息), 我们需要知道其中有几个是大于几个是大于等于. 一个数前面是小于当且仅当是另一个数直接插入到自己前面, 于是用平衡树维护序列即可.
平衡树不断插入有些麻烦, 反过来变成删除即可.
CF1536F Omkar and Akmar
两个人在一个长度为 $n$ 的环上放黑白棋, 每个人在一个空格子里放一个颜色不能与相邻棋子相同的棋子, 问如果两人都采用最优策略, 可能的游戏过程有多少种.
$n\le 10^6$
手玩几组发现后手好像总会赢.
结论是:后手只要走, 无论怎么走都赢. 因为最后一定是若干个黑白交替连续段中间夹着单个空格, 且空格两边颜色一定不同. 所以总棋子数一定是偶数. 所以这俩人实际上是随便走, 然后后手能赢.
于是就可以直接计数最后的局面再乘一个排列.
最后的排列数也很好算, 枚举空格个数, 方案数就是
$$
2n\sum_i \binom{n-i}{i} (n-i-1)!
$$
阶乘减一是因为前面方案数实际上是 $\dfrac{\binom{n-i}{i}}{n-i}$ , 因为插板插完是个环.
CF1111D Destroy the Colony
什么鬼题面
给一个字符串 $s$ , $q$ 次询问对于两个字符 $x, y$ , 任意重排 $s$, 有多少种方法可以使得每一种字符都只出现在 $s$ 的前一半或后一半, 并且 $x, y$ 处于同一边.
$\vert s \vert \le 10^5, \vert \Sigma \vert \le 52, q\le 10^5$
首先 $q\le 10^5$ 是在诈骗, 一共只有 ${ \vert \sigma \vert }^2$ 种询问.
设 $n=\dfrac{ \vert s \vert }{2}$
考虑没有限制的话, 就是要我们从中选若干个数和为 $n$ 求方案数, 这个方案数乘上 ${(m! )}^2$ 再除掉 $\prod cnt_i!$ 就是没限制的答案. 有限制的时候就用从背包里删物品的做法删了再加进去一个他俩算作同一种的即可.
CF1466G Song of the Sirens
给定字符串 $s_0, t$ , 满足 $s_{i+1}=s_it_is_i$ . 多次询问, 每次询问字符串 $w$ 在指定的 $s_k$ 中的出现次数. 答案对 $10^9+7$ 取模.
$n, q\le 10^5$
考虑 $s_i$ 对询问的贡献是跨过 $t_i$ 的出现次数, 长度是 $2\vert w\vert +1$ , 用kmp, hash可以做到 $k\vert w\vert$ 回答单次询问.
那么考虑, 对于 $i, j$ , 如果 $\vert s_i\vert >\vert w\vert, \vert s_j\vert >\vert w\vert, t_i=t_j$ , 它们的贡献应该相同.
而由于每次 $s$ 长度翻一倍, 只用 $\log w$ 次就超过了, 那么复杂度就是 $\min{\log w, k} \vert w\vert$ . 结束了.
CF1400G Mercenaries
有 $n$ 个人和 $m$ 对敌对关系, 每一个人有一个条件区间 $[l_i, r_i]$ .
现在要在这 $n$ 个人中选若干个人. 定义一个合法的选择 ${S}$ , 当且仅当对于 ${S}$ 中的所有人 $i$ , $l_i\le \vert S \vert \le r_i$ , 且 ${S}$ 中所有人互不敌对.
求有多少种合法的选择, 答案对 $998244353$ 取模.
$1\le n\le 3\times 10^5$ , $0\le m\le \min{20, \frac{n(n-1)}{2}}$ , $1\le l_i\le r_i\le n$ .
考虑如果 $m=0$ , 直接枚举选的人数就做完了.
考虑容斥, 于是要求满足不限制集合 $s$ , 那么就是强制选若干点的方案数.
那么若原来我们枚举人数 $x$ 的时候方案数是 $\binom{n}{x}$ , 现在强制选了 $cnt$ 个点, 方案数就是 $\binom{n-cnt}{x-cnt}$
要对所有这个求和会寄, 但因为这个 $cnt$ 最大到 $2m$ , 所以可以直接一遍处理所有 $cnt$ , 再一遍容斥枚举点集 $O(1)$ 算, 复杂度就是 $nm+2^m$ .
CF285E Positions in Permutations
称一个 $1\sim n$ 的排列的完美数为有多少个 $i$ 满足 $\vert P_i-i \vert =1$ .
求有多少个长度为 $n$ 的完美数恰好为 $m$ 的排列. 答案对 $10^9+7$ 取模.$1 \le n \le 1000, 0 \le m \le n$ .
二项式反演. $f(n)$ 表示完美数至少为 $k$ 的方案数, $g(n)$ 表示恰好为 $k$ 的, 于是有 $f(n)=\sum_i \binom{i}{n} g(i)$ , 反演后 $g(n)=\sum_i {(-1)}^{n-i}\binom{i}{n} f(i)$ .
现在转而求钦定 $k$ 个完美位的方案数. 考虑dp. $f_{i, j, 0/1, 0/1}$ 表示值域上前 $i$ 个选了 $j$ 个, 且 $i, i+1$ 是否作为完美位, 复杂度 $n^2$ 然后乘上一个阶乘就上上文的 $f(n)$ , 反演掉即可.
CF1530F Bingo
给定一个 $n\times n$ 的表格, 表格中的每个元素有 $p_{i, j}$ 的概率为 $1$ , 否则为 $0$ .
求至少有一行或一列或一条对角线全为 $1$ 的概率. 对角线指主对角线或副对角线.
$n\le 21$
对角线看做特殊的列.
考虑容斥, 复杂度 $n\times 2^{2n+2}$ , 是不行的.
考虑只容斥列, 对于行带着容斥系数dp. 那么钦定一些列选不选之后, 这一行的系数就是没有被强制选的部分的概率的乘积, 设为 $p$ , 注意因为带着系数, 多选这一行之后应该乘 $-1$ , 两个加起来就行了.
CF1486F Pairs of Paths
给定一棵树和树上若干条路径, 求有多少个对 $i\ne j$ 满足路径 $i$ 和路径 $j$ 有且仅有一个公共点.
$n\le 3\times 10^5$
一开始糊了个强力做法, 假了, 不会.
考虑两个路径的交点一定是两个路径的lca中深的那一个.
考虑如果两个lca相同, 问题是简单的: 统计lca相同, 且路径经过的子树不同, 只要容斥算相同的就行了.
不同的做法感觉很鬼, 说的是LCA从小到大排序, 每次给小于当前lca的lca点的子树加1. , 查的时候查一下, 以lca为根的子树和减去序列两段点子树和.
另一个做法是离谱的点边容斥.
CF140E New Year Garland
现在小 $A$ 手上有 $m$ 种小球, 他要用这些小球装饰一棵圣诞树.
这是一棵神奇的圣诞树, 一共有 $n$ 层, 每层由 $l_i$ 个小球组成.
对于每一层内部, 相邻的小球的都不相同.
同时, 外部来看, 相邻的两层的小球集合不相同.
现在小 $A$ 想要知道一共有多少种合法装饰方案, 答案对 $p$ 取模.
数据范围: ( $1\le n, m\le 10^6, 2\le p\le 10^9, 1\le l_i\le 5000, \sum\limits^n_{i=1}l_i\le 10^7$ )
考虑对于一层的计数方案, 只取决于这一层能用的颜色数和这层的球总数. 数量是 $m\times (m-1)^{c-1}$ , $c$ 为能用的数量.
那么差分完了就是恰好用 $c$ 种的, 设这个为 $g(l, c)$
那就直接 $f_{i, j}$ 表示前 $i$ 层, 最后一层用了 $j$ 个颜色, 就行了吧.
$$
f_{i, j} = (\sum f_{i-1, k}) \times {m}^{\underline{j}}\times g(l_i, j) - f_{i-1, j}\times j! \times g(l_i, j)
$$
然后发现我是智障, $g(l, c)$ 不能用至多的差分得到, 关系是一个二项式反演, 这个 $g$ 还是直接递推比较好. 式子是 $g(i, j)=g(i-1, j-1)+g(i-1, j)\times (j-1)$
P5204 [USACO19JAN] Train Tracking 2 P
给出长 $n$ 的序列的每个区间 $[i, i+k-1]$ 的最小值, 求值域不超过 $10^9$ 的原序列 $a$ 的方案数, 膜 $10^9+7$ .
$n, k\le 10^5, a\le 10^9$
考虑假设所有 $c$ 都是相同的, 怎么做? 相当于每 $k$ 个就要选一个 $c$ . 然后我们设可以选的数总数是 $x+1$ (多了个 $c$ )
暴力dp就是 $f_{i, j}$ 表示前 $i$ 个, 且没选 $c$ 已经有 $j$ 个. 转移 $f_{i, j}=f_{i-1, j-1}\times x, f_{i, 0}=\sum f_{i-1, j}$ , 可以直接记录一下上移多少位和全局乘法标记. 就是通过数据结构优化dp做.
题解区一个老哥用等差数列写了一把, 惊叹于他的脑回路, 但还是应该积累一下这个方法, 就是对一维状态的dp可以用类似数列的方法做.
最后, 实际上可以法法塔, 是1log的.
当然重点是接下来的, 考虑 $c$ 分成若干段, 对于每个连续段, 考虑 $c_i=\ldots=c_j$ , 那么现在有 $c_{i-1}>c_i$ , 就有:
$\min {a_i\ldots a_{i+k-1}}=c_i<c_{i-1}=\min {a_{i-1}\ldots a_{i+k-2}}$
于是有 $a_{i+k-1}=c_i$ 确定下来了, 那么它前面的都可以随便选, 直接归到上一个连续段考虑即可. 后面相同的同理. 这样处理之后每一段是独立的, 最后直接乘起来就是答案. 如果一段空了那么显然不用管它们.
P3643 [APIO2016] 划艇
计数长 $n$ 的序列 $a$ , 满足要求
- 若 $a_i\ne 0, a_i\in [l_i, r_i]$
- 若 $a_i\ne 0, a_i\ge a_{i-1}$
$n\le 500, a_i\le b_i\le 10^9$
和上面CF1295F Good Contest类似吧.
仍然离散化区间, 设 $f_{i, j}$ 表示前 $i$ 个, 最后一个是 $j$ 区间的方案数, 然后不从 $i$ 转移而从 $j$ 转移, 就结束了.
CF367E Sereja and Intervals
有 $n$ 个区间, 你需要为每个区间分配左右端点, 端点属于 $[1, m]\cap \mathbb{N}$ . 你需要保证区间两两互不包含且至少存在一个区间的左端点等于 $x$ , 输出方案数对 $10^9+7$ 取模的结果, 区间有标号. $nm\leqslant 10^5$ , $1\leqslant x\leqslant m$ .
还可以吧.
考虑很显然的因为不互相包含, 所以按 $l$ 排序之后 $r$ 递增.
于是方案数是左右端点分别的方案再给一个阶乘(标号).
然后这个可以直接dp. 就直接设 $f_{i, j, k}$ 前 $i$ 个有 $j$ 个左端点 $k$ 个右端点. 复杂度就 $nm^2$
P6189 跑步
划分数. $n\le 10^5$ , 对 $p\le 2^{30}$ 取模.
多项式? ? ?
居然是根号分治. 设 $B=\sqrt n$
完全背包前 $B$ 个数的方案, 记结果 $g_{i}$ 表示凑 $i$ 的方案数.
dp出只有大于 $B$ 的数凑成的方案, 然后卷起来.
CF1651E Sum of Matchings
收录在greedy里
CF1613F Tree Coloring
给一棵有根树, 求排列 $c$ 的方案数使得 $\forall u, \ c_{fa}-1\ne c_u$ .
膜998244353, $n\le 250000$
原来是多项式题.
考虑钦定 $i$ 个点不合法, 直接容斥就是 $i$ 为偶数的方案减去奇数的.
二项式反演也一样. 考虑钦定 $i$ 个点不合法的方案数是 $f(i)$ , 恰好 $i$ 个点不合法的方案数 $g(i)$ , $f(i)=\sum \binom{i}{j}g(j)$ , 这个是因为 $i$ 个点不合法的方案是等价的, 于是反演得 $g(0)=\sum f(i)\times (-1)^i$ , 可以扩展到其它恰好其它 $i$ 个不对的.
那么考虑如何求 $f_i$ . 我们只需要知道从这里面选 $i$ 个不合法的方案数, 因为剩下的可以随便排, 问题就变成了钦定 $i$ 个点不合法的方案数.
考虑点 $u$ 有 $k$ 个儿子, 则在其中钦定一个不合法点的方案数是 $k$ , 钦定其中没有的方案数是1, 所以把 $1+kx$ 卷起来就行了. 分治ntt可以做 $n\log^2 n$ .
CF1580B Mathematics Curriculum
求有多少排列长度为 $n$ , 恰有 $k$ 个数满足所有包含这个数的区间中, 不同的最大值有恰好 $m$ 个.
$n\le 100, m, k\le n, p\le 10^9$
[trick] 对于一个数来说, 其包含这个数的区间的不同最大值个数恰好是这个数向前向后的前缀min个数之和. 而这个等价于笛卡尔树(大根)上的层数, 所以就是计数笛卡尔树上 $m$ 层恰好有 $k$ 个元素的方案数.
考虑dp笛卡尔树的结构, 设 $f_{i, j, k}$ 表示 $i$ 个点的笛卡尔树, 深度为 $j$ 的有 $k$ 个的方案数即可.
CF1278F Cards
有 $m$ 张牌, 其中一张是王牌, $n$ 次洗牌后查看第一张牌, 看见王牌的次数 $x$ . 认为洗牌时 $m!$ 排列概率均等. 求 $x^k$ 的期望.
$n, m\le 998244353, k\le 5000$
直接推式子.
$$
\begin{aligned}
&\sum_i i^k\binom {n}{i}{(\dfrac{1}{m})}^i{(\dfrac{m-1}{m})}^{n-i} \
=&\dfrac{1}{m^n}\sum_i i^k{(m-1)}^{n-i}\binom{n}{i}\
=&\dfrac{1}{m^n}\sum_i {(m-1)}^{n-i}\binom{n}{i}\sum_j {k\brace j}i^{\underline{j}}\
=&\dfrac{1}{m^n}\sum_j{k\brace j}\sum_i{(m-1)}^{n-i}\binom{n}{i}i^{\underline{j}}\
\
&\binom{n}{i}i^{\underline{j}}=[i\ge j]\dfrac{n^{\underline{i}}}{i^{\underline{i}}}i^{\underline{j}}=\dfrac{n^{\underline{j}}{(n-j)}^{\underline{i-j}}}{(i-j)! }=n^{\underline{j}}\binom{n-j}{i-j}\
\
&\sum_i {(m-1)^{n-i}}\binom {n}{i}i^{\underline{j}}\
=&n^{\underline{j}}\sum_i \binom{n-j}{i-j}{(m-1)^{n-i}}\
=&n^{\underline{j}}\sum_i \binom{n-j}{n-i}{(m-1)^{n-i}}\
=&n^{\underline{j}}{(m+1-1)}^{n-j}\
=&n^{\underline{j}}m^{n-j}\
\
&\dfrac{1}{m^n}\sum_j{k\brace j}\sum_i{(m-1)}^{n-i}\binom{n}{i}i^{\underline{j}}\
=&\dfrac{1}{m^n}\sum_j{k\brace j}n^{\underline{j}}m^{n-j}
\end{aligned}
$$
可以枚举 $j$ 直接做了.
告诉我们要相信式子的力量.
CF1153F Serval and Bonus Problem
给定长为 $l$ 的数轴, 有 $n$ 个在 $[0, l)$ 间随机的区间, 求被被至少 $k$ 个区间覆盖的期望长度.
$k, n\le 2000, l\le 10^9$ , 膜998244353.
首先实际上 $l$ 是没用的, 按 $l=1$ 的算直接乘上就行了.
考虑位置 $x$ 被覆盖一次的概率是 $2x(1-x)$
$$
f(x)=\sum_{i\in[k, n]} \binom{n}{i}(2x(1-x))^{i} (1-2x(1-x))^{n-i}
$$
对这个求积分就是答案.
这个是关于 $x$ 的多项式, 如果直接暴力是 $n^3$ 的.
中间部分是卷积, 可以 $ntt$ 做成 $n^2\log n$ .
考虑算点值再插值回去, 最后再求积分也是可行的, 那么 $O(n^2)$ 算 $n$ 个点值就行了.
好厉害啊.
CF814E An unavoidable detour for home
$n$ 个点, 每个点有度数 $d_i$ , 构造无向图满足点 $1$ 到点 $i$ 的最短路唯一且比到 $i-1$ 的长. 求方案数.
$n\le 50, 2\le d_i\le 3$
想想以1为根的最短路树. 那么图是这个的基础上连若干同深度的边得到的.
然后dp计数. 设 $f_{i, j}$ 表示后 $i$ 个节点, 最后一层有 $j$ 个的方案数.从下往上dp.
这里不记点的度数, 因为从下往上dp保证每个点都还有一个度留给往上的. 每个点的儿子数量不确定但父亲数量确定是从下往上的原因.
那么相邻两层之间的边, 一层内的边都分别预处理即可.
反正还是很不会数数啊.
[think] 想不到原因的话, 感觉还是枚举dp方向吧.
CF382E Ksenia and Combinatorics
求有多少个以 $1$ 为根的 $n$ 节点二叉树最大匹配为 $k$ , 树相同判定为每个节点的相连节点相同.
膜 $10^9+7$
第一反应是, 很像SDOI2022D2T1吧
所以还是类似dp of dp的思路, 但注意树的最大匹配是不需要dp的, 实际上做法是直接贪心, 从叶子开始匹配, 那么这里就设 $f_{u, i, 0/1}$ 表示 $u$ 节点内有 $i$ 个匹配, 其中 $u$ 自身是否被匹配即可.
注意因为判定是树同构所以钦定左儿子小于右儿子, 大小相同除以2. 并且转移的时候要带编号.
CF235E Number Challenge
一个莫反题有贪心和组合数学标签上让人问号的.
收录在greedy中.
CF1548C The Three Little Pigs
$q$ 次给定 $x$ , 询问 $\sum_{i=1}^n \binom{3i}{x}\pmod {10^9+7}$ .
$n\le 10^6, q\le 2\times 10^5, x\le 3n$
考虑那一定是对着这一堆 $x$ 一起算. 但这个式子关于 $x$ 不是多项式.
但还是简单的, $\binom{3i}{x}=[z^x] (z+1)^{3i}$ , 那么直接求和然后暴力求即可求出对所有 $x$ 的答案.
CF840C On the Bench
给定序列 $a_n$ , 求排列个数使得相邻两个的乘积不为完全平方数. 膜 $10^9+7$ .
$n\le 300, V\le 10^9$
考虑直接给所有数除掉自己的平方因子, 就成了求相邻两数不同的排列个数.
考虑把所有类的数一一插进去, 假设现在已有的排列长 $m$ , 要再插进 $k$ 个相同值, 方案数显然是 $\binom{m+1}{k}k!$ . 就结束了吧
哦暴露了垃圾的数数水平, 这个显然是错的啊原因是有可能出现现在有若干个位置相邻但以后被插入了东西.
那就再加一维, 逐个数字dp直接记 $f_{i, j, k}$ 表示前 $i$ 类数, 并且当前有 $j$ 个相邻的数之间需要被插入新的数, 其中有 $k$ 个是等于 $i$ 的, dp就行了. 复杂度是 $n^3$ 的. 这个dp转移比较像那种连续段dp.
有个更厉害点的做法, 考虑仍然容斥, 那么钦定 $i$ 对彼此相邻的方案数记为 $f_i$ , 那么显然答案就是 $\sum f_i\times (-1)^i$ , 而 $f_i$ 可以由各个颜色的直接卷积合并. 复杂度 $n^2$ .
CF997C Sky Full of Stars
给定 $n\times n$ 的正方形网格, 用三种颜色染色, 求没有一行或一列颜色相同的方案数. 膜998244353.
$n\le 10^6$
看到这种直接考虑容斥反演类技术. 于是钦定选了 $i$ 行 $j$ 列颜色相同方案数是 $f(i, j)$ , 没有相同的方案数就是
$$
\sum_i \sum_j f(i, j)\binom{n}{i}\binom{n}{j}\times (-1)^{i+j}
$$
(高维容斥反演时系数是各维度之积, 也可以分部理解)
考虑 $f$ 是十分容易计算的:
$$
f(i, j)=
\begin{cases}
3^{(n-i)(n-j)+1}, \ ij\ne 0\
3^{i+j}3^{n(n-i-j)}\ ij=0
\end{cases}
$$
发现 $ij=0$ 的情况可以直接单独计算(此时只有一个变量, 直接暴力求). 考虑 $ij\ne 0$ 的情况:
$$
\begin{aligned}
&\sum_i \sum_j \binom{n}{i}\binom{n}{j}\times (-1)^{i+j}\times 3^{(n-i)(n-j)+1}\
=&\sum_i \sum_j \binom{n}{i}\binom{n}{j}\times (-1)^{i+j}\times 3^{ij}3^{ni}3^{nj}3^{n^2+1}\
=&3^{n^2+1}\sum_i (-1)^i \binom{n}{i}3^{ni} \sum_j \binom{n}{j}(-1)^j\times 3^{nj}\times 3^{ij}
\end{aligned}
$$
$ij$ 不会处理了. 大多数组合恒等式这里不行因为这个次幂很难看, 考虑少数有正常幂的二项式定理
$$
\begin{aligned}
&3^{n^2+1}\sum_i (-1)^i \binom{n}{i}3^{ni} \sum_j \binom{n}{j}(-1)^j\times 3^{nj}\times 3^{ij}\
=&3^{n^2+1}\sum_i (-1)^i \binom{n}{i}3^{ni} \sum_j \binom{n}{j}(-1\times 3^{n+i})^j\
=&3^{n^2+1}\sum_i (-1)^i \binom{n}{i}3^{ni} (-1\times 3^{n+i}+1)^n
\end{aligned}
$$
就结束了.
CF1327F AND Segments
给定 $n, k, m$ 以及 $m$ 个限制 $(l_1, r_1, x_1)\ldots (l_m, r_m, x_m)$
求每个数都在 $[0, 2^k]$ 中, 且 $\forall i, a_{l_i}\mathrm{and} a_{l_i+1}\mathrm{and}\ldots a_{r_i}=x$ , 且长度为 $n$ 的序列个数
$n, m\le 5\times 10^5, k\le 30$
膜998244353
考虑每一位是相同的. 问题变成了, 指定一段全是1或者其中至少有一个0, 求方案数.
那直接用全1段把它们拆成若干段, 每段就只有限制至少有一个0的方案了.
可以设 $f_i$ 表示前 $i$ 个且第 $i$ 个为0的方案数, 则 $f_i$ 是一个区间的和, 前缀和优化即可.
CF1174E Ehab and the Expected GCD Problem
关于排列 $p_n$ , 设 $g_i$ 表示 $\gcd {a_1, a_2, \ldots, a_i}$ , $g_i$ 的数量为 $f(p)$ , $f$ 的最大值为 $f_{max}$ , 求有多少个排列 $p$ 满足 $f(p)=f_{max}$
$n\le 10^6$
考虑 $f$ 的最大值, 显然一种构造是从头开始2的幂下降一定能达到最大. 于是最大值已知.
那么也能顺便得到结论: 不会有 $5$ 及以上的下降(下降指前缀 $\gcd$ 除以了 $5$ ), 不会有两个 $3$ 的下降, 因为都可以调整为数量更多的 $2$ 下降.
于是直接dp, $f_{i, j, k}$ 表示前 $i$ 个, 其中当前gcd为 $2^i3^j$ 的方案数, 从序列维转移.
dp排列值域扫多了都要忘了能序列了.
CF1367F Flying Sort
给定 $n$ 个正整数构成的序列, 每次可以将序列中的任意一项放到最前面或最后面, 求最少操作次数让序列不降.
Easy Version
保证每个数互不相同, $n\le 3000$
每个数最多操作一次. 显然.
那么找到可以保留的最多的数. 并且因为中间不能插进数, 所以就是保留最长的相差为1的上升的子序列. 设 $f_i$ 表示前 $i$ 个以 $i$ 结尾的答案, 那么 $f_{a_i}=f_{a_i-1}+1$
Hard Version
可以有相等的数, $n\le 2\times 10^5$
首先你觉得这个就是直接把上面的dp搬过来, 加上可以相等.
但实际上区别在于, 中间可能要取完, 比如排列1 1 2 2 3 3 2中, 我们不能选1 1 2 2 3 3因为这样2是插不进来的.
所以就是分三种情况: 都等于一个值, 两段不一定取完, 三段, 其中中间段必须取完这三种, dp即可.
CF510D Fox And Jumping
给出 $n$ 张卡片, 分别有 $l_i$ 和 $c_i$ . 在一条无限长的纸带上, 你可以选择花 $c_i$ 的钱来购买卡片 $i$ , 从此以后可以向左或向右跳 $l_i$ 个单位. 问你至少花多少元钱才能够跳到纸带上全部位置. 若不行, 输出 $-1$ .
$n\le 300, l_i\le 10^9$
能从0到1等价于能完成任务. 考虑若干数凑出1等价于它们 $\gcd$ 为1, 直接冲用map记状态就行.
BZOJ3864 Hero meet devil
给定 $s$ , 求有多少长 $m$ 的串 $t$ 满足 $lcs(t, s)=i$ , 对所有 $i$ 输出答案.
$\vert s\vert \le 15, m\le 1000$
内层dp显然是求lcs的dp $f_{i, j}$ 表示 $s$ 前 $i$ 个和 $t$ 前 $j$ 个那个, 是众所周知的, 关键是如何压缩状态.
发现做到 $2^{\vert s\vert}m$ 左右可能正好? 考虑我们显然扫描 $j$ , 维护所有 $f_{i}$ , 和LCS Again那题一样有个经典结论 $f_{i, j}-f_{i, j-1}\le 1$ 所以可以差分压成二进制就做完了.
CF1043F Make It One
给定序列 $a_n$ , 求选最少的数使得它们gcd为1.
$n, a_i\le 3\times 10^5$
考虑 $3\times 10^5$ 内的数的最多不同质因数个数有 $6$ 个.
那么答案最大是不是不超过 $6$ 呢.
发现实际上界是7, 构造出来应该是 $2, 3, 5, 7, 11, 13, 17$ 分别删去一个数得到的集合.
qyc给出强力做法: 直接gcd卷积, 若答案为 $k$ , 则卷恰好 $k$ 次的时候 $f_1\ne 0$ .
复杂度是 $n\log n$ 或 $n \log^2 \log n$
CF1792F1 Graph Coloring (easy version)
给定 $n$ 个点的完全图, 求有多少个红蓝染色方案, 使得对任意一个点集 $S$, 满足其导出子图仅看红色边是连通的, 或满足仅看蓝色边上连通的, 但不同时满足两个限制.
$n\le 5000$
行
[trick] 一个图和它的补图中至少有一个是连通的.
对于原图中不连通的两个联通块, 其中一个的点 $x$ 必然和另一个的所有点相连, 所以这个连通块在补图中是连通的, 剩下部分显然.
整张图必然是蓝/红连通的, 假设是红连通, 蓝不连通.
那么考虑计数策略之一, 看所有和 $1$ 蓝连通的点组成的块, 组成了一个规模更小的问题, 而剩下的点和这个块之间全是红边, 剩下的点是另一个规模更小的问题, 可以 $n^2$ dp出来.
$$
f_n=\sum_{x<n} \binom{n}{x} f_x \cdot (f_{n-x}\cdot (2-[x=n-1]))
$$
$n-x$ 的部分可能是蓝连通的也可能是红连通的, 但当只有一个点的时候就只有一种了.
CF1781F Bracket Insertion
进行 $n$ 次操作, 设当前序列为 $s$(初始为空), 每次从 $s$ 中随机选一个空位(若长度为 $k$, 有 $k+1$ 个空位), 以 $p$ 概率插入
()或以 $1-p$ 概率插入)(, 求最后得到合法序列的概率.膜 $998244353$.
$n\le 500$.
考虑把插入的包含关系建树, 设()是 $1$, )(是 $-1$, 看起来要求任意根开始的路径和非负.
那考虑dp, 设 $f_{i, j}$ 表示 $i$ 个点, 节点到当前根的和最小为 $j$ 的方案数dp应该就行.
todo;
CF1750F Majority
求有多少个01串 $s$, 满足允许任意次把一个1个数大于等于0个数, 且两端点是 $1$ 的区间变成全1的操作下, 变成全1串.
对 $m$ 取模.
$n\le 5000, m\le 10^9$.
看起来是让你dp的, 并且我们显然应该对着操作完了不能操作了的串dp.
容易发现操作完了的串是0, 1连续段交替, 且0的长度大于两边1的长度, 当然两头必须是1.
于是设 $f_{i, j}$ 表示长度为 $i$, 操作完最后一个1段长 $j$ 的方案数, 你发现 $f_{i, j}, j<i$ 的转移方式是能写的, 考虑去掉结尾 $j$ 个 $1$, 再枚举去掉 $k$ 个 $0$, 再枚举剩下的最后长 $l$ 个 $1$ 即可. 而 $f_{i, i}$ 十分遗憾的等于自身
于是 $f_{i, i}$ 的用 $2^{i-2}-\sum f_{i, j}$ 表示了.
用一些前缀和优化做到 $n^2$.
CF1617E Christmas Chocolates
你有一个长度为 $n$ 的数组 $a_1, a_2, \dots, a_n$, 一开始数组中的所有元素都互不相同.
你可以选择两个数组中的元素 $a_x, a_y$, 然后执行若干次操作, 每次操作你可以选择一个非负整数 $k$, 然后将 $a_x$ 替换为 $2^k-a_x$. 如果在某次操作之后 $a_x=a_y$, 那么不再执行操作. 任意时刻, $a_i$ 不能为负数.你是一个很聪明的人, 所以在选择一对 $(x, y)$ 之后你知道如何用最少的操作次数使得 $a_x=a_y$. 但是你并不满足于此, 你现在还想知道使得最少操作次数最大的 $(x, y)$. 请求出 $x, y$ 和这个最大的最少操作次数 $m$.
数据范围:
- $2\leqslant n\leqslant 2\times 10^5$.
- $0\leqslant a_i\leqslant 10^9$.
考虑一个数经过操作形成一棵树(对于一个树, 只有最小的 $k$ 变成的数小于自己). 于是路径是唯一的, 要求最长路.
求虚树需要求lca, dfn, 完全不会啊.
停, 一个点的深度是 $\log v$ 的, 那么根据直径性质就直接求最远的点, 再求最远的点就做完了.
CF1574F Occurrences
有 $n$ 个值域在 $[1, k]$ 的数列 $A_1, A_2, \cdots, A_n$, 要求构造一个长为 $m$ 的值域在 $[1, k]$ 的序列 $a$, 满足对于所有数列 $A_i$, $A_i$ 在序列 $a$ 中的出现次数大于等于其任意一个非空子段在 $a$ 中的出现次数.
求不同的 $a$ 的数量, 答案 $\bmod 998244353$.
数据范围: $1\le n, m, k\le 3\times 10^5, \sum c_i\le 3\times 10^5$.
考虑限制的意思是, 如果 $a$ 中的一个数出现了, 那么 $a$ 必须按顺序完整出现一遍.
于是对于 $i, j$, $A_{i, j}\to A_{i, j+1}$ 连边, 要求每次可以选择一个入度为 $0$ 的点走一条链拼出整个串.
那后面这个问题背包求方案数啊.
CF1542E Abnormal Permutation Pairs
给定 $n, m$, 求有多少对长度为 $n$ 的排列 $p, q$, 满足以下条件.
- $p$ 的字典序小于 $q$
- $p$ 的逆序对个数大于 $q$.
答案对 $m$ 取模.
$1\le n\le 500, 1\le m\leq 10^9$,不保证 $m$ 为素数.
容易想到枚举前面相同的前缀长度, 也容易想到笛卡尔树dp排列.
那么注意到, 枚举一个相同的长 $l$ 前缀后, 只要看后面的逆序对数就能比较.
于是dp后面的, $f_{i, j, 0/1/2}$ 表示从小到大插入 $i$ 个数, 目前两个排列逆序对个数的差为 $j$, 第一个数现在是 $p/q/$ 一样大的方案数. 如果枚举插入位置复杂度是 $n^5$ 的吧.
然后考虑从 $f_{i, j}$ 转移到 $f_{i+1, j+k}$ 时, $k$ 是插入的两个数的位置的下标的差, 于是就是乘一个 $n-\vert k\vert+C$ 的系数.
那么用一些奇妙的二阶差分就能区间加等差数列了吧, 或者把 $k$ 拆成 $(j+k)-j$ 后在两边分别贡献.
复杂度 $n^3$.
Froggy的”显然生成函数是”, 就是直接考虑每次插入一个 $i$ 时的贡献, 则插入到一个序列相当于把原答案卷上 $\sum_{j=0}^{i-1} x^j$, 再插入就是又卷 $\sum_{j=0}^{i-1} x^{-j}$, 把这两个乘起来化简即可.
CF1511F Chainword
给出一个 $n$ 个词的字典 $S_1, S_2, \dots , S_n$, 求由长度均为 m 的字符串
S 和划分 $P, Q$ 组成的三元组 $(S, P, Q)$ 数量, 满足:
- 对于 $P$ 中划分的每一段 $[l, r]$, 均满足 $S[l, r]$ 在字典中.
- 对于 $Q$ 中划分的每一段 $[l, r]$, 均满足 $S[l, r]$ 在字典中.
答案对 $998244353$ 取模.
$n\le 8, m\le 10^9$
先考虑 $O(mC)$ 的东西, 那么dp过程中看起来我们需要记录最后几位的是啥, 但实际上显然只关心匹配情况, 所以就是都插到字典树里, $f_{i, j, k}$ 记录一共长 $i$, 当前 $P$ 在字典树的 $j$, $Q$ 在字典树的 $k$.
然后显然和 $i$ 没啥关系, 就矩阵快速幂.
8个字符串, 每个有5个字符, 最大有 $40$ 个节点, 复杂度爆炸了.
观察性质, $j, k$ 都是当前填好的后缀, 所以他俩一个是另一个的后缀.
于是现在状态数减少到 $588=320$, 过了.
[trick] 同一个字符串的两个后缀必有一个是另一个后缀
CF1487G String Counting
你有 $26$ 个不同的字符, 第 $i$ 个字符有 $c_i$ 个($\frac{n}{3} < c_i \leq n$).
你希望用这些字符, 构造出一个长度为 $n$ 的字符串(每个字符在字符串中出现的个数不超过 $c_i$), 使得这个字符串上不存在长度为奇数且大于 $1$ 的回文串. 求出方案数对 $998244353$ 取模的结果.
$n\le 400$, 10s, 1G
注意到 $\frac{n}{3}<c_i\le n$ 的意思是, 你只能有两个字符超出限制.
那么先不考虑字符数限制的话, 考虑添加一个字符 $c$ 时只要求它不能和上上次添加的相同即可, 是随便做.
那么容斥, 钦点两个字符次数过多, 于是 $f_{i, j, k, 0/1/2, 0/1/2}$ 表示添加 $i$ 个字符, 如果 $a, b$ 的次数分别是 $j, k$, 最后两个位置是 $a/b/$ 其他的情况下的答案. 仍然可以转移.
CF1540C1/2 Converging Array
这是这道题的困难版, 与简单版唯一不同是 $1 \le q \le 10^5$
现在有长度为 $n$ 的数组 $a$ 和长度为 $n - 1$ 的数组 $b$, 进行无穷次如下过程直至 $a$ 数组值收敛
- 选择一个数字 $i$
- 同时使 $a_i = min(a_i, \frac{a_i + a_{i + 1} - b_i}{2}), \ a_{i + 1} = max(a_{i + 1}, \frac{a_i + a_{i + 1} + b_i}{2})$ (没有取整)
定义 $F(a, b)$ 为操作完成后 $a_1$ 的值
现在你知道数组 $b$ 和 长度为 $n$ 的数组 $c$, 保证 $\forall i \in [1, n], \ 0 \le a_i \le c_i$
有 $q$ 组询问, 每次问使 $F(a, b) \ge x$ 的数组 $a$ 有多少个
答案对 $1\ 000\ 000\ 007$ 取模
考虑简单版($q=1$).
考虑操作就是, 对于 $a_i, a_{i+1}$, 如果 $a_{i+1}<a_i+b_i$ 就把它们两个以平均值为中心差调整到 $b_i$
考虑现在的限制, 因为一个前缀的和随操作是不增的, 再通过分析收敛后, $a_i\ge x+\sum_j b_j$, 容易得出前缀和 $s_i\ge ix+\sum b_j$.
问题来到充分性, 考虑如果一开始 $a_1>x$, 那么要让它调整到小于 $x$ 必须让 $a_2<x+b_i$, 以此类推.
那么 $q=1$ 是简单背包, 可以优化到 $n^3$
那么注意到通过分析 $a_1, a_n$ 的取值范围, 得出不同的 $x$ 只有 $200$ 种(剩下都不可能), 就过了.
4. 2021sdpttday3
AGC028B
现在有 $N$ 条线段排成一行, 其中第 $i$ 条线段的长度为 $A_i$. 现在要按照一个顺序删除所有线段, 以下定义其代价:
- 相邻的没有被删除的线段会连在一起.
- 删除连起来的一些线段中的任意一条线段, 花费的代价为这些线段的总长.
- 一个删除顺序的代价, 就是每条线段的删除代价总和.
对于所有 $1, 2, \cdots, N$ 的排列 $p_1, p_2, \cdots, p_N$, 求依次删除 $p_1, p_2, \cdots, p_N$ 的代价之和. 答案对 $10^9+7$ 取模.
$N\leq 10^5, 1\leq A_i\leq 10^9, 2s, 1GB$.
考虑一条线段的贡献, 也就是其在删除时间的笛卡尔树上深度, 只要考虑一个点是它祖先的概率, $i$ 是 $j$ 的祖先要求 $i$ 被删的时候区间 $[i, j]$ 保留, 就是 $\dfrac{1}{\vert i-j\vert +1}$, 累加起来就是祖先概率, 就会做了.
CF605E Intergalaxy Trips
给定一张 $n$ 个点的图, 目标是花费最小的天数从 $1$ 到 $n$.
每一天, 都有 $p_{ij}$ 的概率存在边 $\langle i, j\rangle$, 花费恰好 $1$ 天.
每天可以选定一条存在的边出发, 也可以选择留在原地不动(即 $p_{i, i}=1$).
求最优策略下的期望天数.
$n\leq 1000, 2s, 256MB$.
$f_u=p_{u, v}f_v+(1-p_{u, v})f_u$
-1. 其他
Nowcoder某题
$n$ 行 $2n$ 列的网格图, 每行每列最多有两个棋子, 求本质不同方案数.
本质相同定义为可以通过交换若干行列得到相同的方案.
$n\le 10^5$ , 膜998244353
汪娟介绍的
考虑这是一个经典网络流模型, 可以把一个方案对应到一个二分图上(建行点列点, 有棋子则连对应行列).
于是变成计数无标号二分图个数, 并且每个点度数不超过2, 一边 $n$ 个点一边 $2n$ 个点.
发现因为度数限制, $n$ 个点这边怎么选 $2n$ 个点都够用, 所以可以只考虑左边的大小, 视右边大小为无限.
那么度数限制为 $2$ 的二分图只有链和环两种. 那么就是计数若干个链和环且左边为 $n$ 个点.
然后在仅考虑左边点的情况, 它们的区别仅在于左边至少一个点(左边点少的链, 左右数量相等的链, 环)或者至少两个点(左边数量多一个的链), 所以写成生成函数就是 $\prod_{i=1} \dfrac{1}{1-x^k} * \prod_{i=2} \dfrac{1}{1-x^k}$
一个简单做法是分治ntt或ln+exp.
常数小做法是五边形数四次方乘 $1-x$ . 复杂度 $n\log n$ .
CF930E Coins Exhibition
有 $k(1 \leq k \leq 10^9)$ 个硬币, 每个硬币有正面朝上和反面朝上两种状态.
现有 $n+m(0 \leq n, m \leq 10^5)$ 个限制条件, 每个限制条件形如 $(l_i, r_i)(1 \leq l_i \leq r_i \leq k)$ . 前 $n$ 个限制条件限制区间 $[l_i, r_i]$ 内至少有一个硬币正面朝上, 后 $m$ 个限制条件限制区间 $[l_i, r_i]$ 内至少有一个硬币反面朝上.
问共有多少种摆放硬币的方案使得所有限制条件都被满足. 答案对 $10^9+7$ 取模.
考虑dp, $k$ 这么大肯定要离散化, 不过先想一个关于 $k$ 线性的东西, 考虑限制是在说一个什么, 序列上数数自然设 $f_{i, 0/1}$ 表示前 $i$ 个最后一个是 $0/1$ 的方案, 那么想到钦点从最近的0/1转移, 于是发现一个限制 $[l, r]$ 中至少一个0等价于对于大于等于 $r$ 的位置其找0的时候需要在 $l$ 之后, 那么前缀和优化就线性了. 最后上一个划艇的套路: 离散化区间即可.
我天, 不会写dp了.
P5492 [PKUWC2018]随机算法
我们知道, 求任意图的最大独立集是一类NP完全问题, 目前还没有准确的多项式算法, 但是有许多多项式复杂度的近似算法.
例如, 小 C 常用的一种算法是:
对于一个 $n$ 个点的无向图, 先等概率随机一个 $1\ldots n$ 的排列 $p[1\ldots n]$.
维护答案集合 $S$ , 一开始 $S$ 为空集, 之后按照 $i=1\ldots n$ 的顺序, 检查 ${p[i]}\cup S$ 是否是一个独立集, 如果是的话就令 $S={p[i]}\cup S$.
最后得到一个独立集 $S$ 作为答案.
小 C 现在想知道, 对于给定的一张图, 这个算法的正确率, 输出答案对 $998244353$ 取模.
考虑枚举排列就是每次选一个点, 一个自然的状态是设 $f_S$ 表示当前已经加入了 $S$ 内的点, 答案是对的的概率. 再设 $siz_S$ 表示 $S$ 点集的最大独立集.
那么 $siz$ 转移显然, 主要考虑 $f$ 的转移.
一开始考虑枚举 $u$, 若 $siz_{S/u}+check(u, S/u)=siz_S$ 则转移过来, 但这个是不对的, $u$ 的相邻点可能贡献了 $S/u$ 的 $siz$, 不如删掉这些相邻点从 $f_T$ 转移过来.
P4705 玩游戏
给定 $a_n, b_n$, 对每个 $k$ 求 $\dfrac{1}{nm} \sum_i \sum_j (a_i+b_j)^k$
$n, m, k\le 10^5$
$$
\begin{gathered}
\sum_i \sum_j (a_i+b_j)^k\
=\sum_i \sum_j \sum_l \binom{k}{l}{a_i}^l{b_j}^{k-l}\
=k! \sum_l \dfrac{1}{l! (k-l)! } (\sum_i {a_i}^l) (\sum_j {b_j}^{k-l})
\end{gathered}
$$
可以看出卷积, 问题变成如何求 $c_k=\sum_i {a_i}^k$, 注意到
$$
\sum_k \dfrac{ {a_i}^k\cdot z^k}{k}=-\ln(1-a_iz)
$$
于是
$$
C(z)=\sum_i -\ln(1-a_iz)=-\ln \prod_i (1-a_iz)
$$
分治FFT算里面的即可.
校内模拟Circle
ehzeux 给了你一个圆, 圆上均等地放着 $2n$ 个点, 其中 35 已经帮你在 $k$ 对点之间连好了线段, 你需要从中选择剩下 $n-k$
对点随意连线段 (每个点只连一条线段), 并求出所有连边方案中联通块的个数总和. 两点联通当且仅当两点在同一
条线段上或两点所属于的线段相交. 答案对 $10^9+7$ 取模.$n\le 300$
考虑看起来是dp
但是区间dp试一试发现进行不下去, 连出去的根本做不到
考虑设 $f_{i, j}$ 表示 $i, j$ 是一个连通块内编号最小和最大的点, $[i, j]$ 中的点都已经经过配对, 此时的方案数.
那么这个连通块出现的次数就是上面那个再乘上剩下的点乱连的方案数.
于是问题来到如何算 $f$, 考虑先在 $[i, j]$ 中乱连, 显然不会连出去, 但与 $i$ 相连的连通块最大值不一定是 $j$, 考虑枚举最大值 $a$, 那么此时分成了两部分, 分别是 $f_{i, a}$ 中的部分加上 $[a+1, j]$ 乱连, 用这个容斥即可.
P5401 [CTS2019] 珍珠
有 $n$ 个在范围 $[1, D]$ 内的整数均匀随机变量.
求至少能选出 $m$ 个瓶子, 使得存在一种方案, 选择一些变量, 并把选出来的每一个变量放到一个瓶子中, 满足每个瓶子都恰好装两个值相同的变量的概率.
请输出概率乘上 $D^n$ 后对 $998244353$ 取模的值. 取模部分说明可参考第一题.
$D\le 10^5$
考虑
$$
\sum_i \dfrac{cnt_i}{2} \ge m\
\leftrightarrow \sum_i (cnt_i \bmod 2) \le 2m-n
$$
钦点 $k$ 个数出现奇数次, 奇数的一个数的EGF是 $\dfrac{e^x-e^{-x}}{2}$, 所以总式子是
$$
\binom{D}{k} n! (\dfrac{e^x-e^{-x}}{2})^k e^{D-k}\
\binom{D}{k} \dfrac{n! }{2^k} \sum_i \binom{k}{i} (-1)^{k-j} e^{D-2k+2j}x
$$
因为 $[x^n]e^ax=\dfrac{a^n}{n! }$, 所以再带进去, 就有了卷积的形式.
然后卷积优化二项式反演.
P3978 [TJOI2015]概率论
对于一棵随机生成的 $n$ 个结点的有根二叉树(所有互相不同构的形态等概率出现), 它的叶子节点数的期望是多少呢?
$n\le 10^9$
~~发现答案是 $n-1$ 个点的二叉树个数乘 $n$ ~~
证明就是, 一个 $n$ 个点的树假设有 $k$ 个叶子, 去掉每一个都得到一个 $n-1$ 个点的树. 考虑每个 $n-1$ 的被算了多少次, 相当于能在多少点底下挂一个叶子, 显然是 $n$, 于是就做完了.
另外EI的拉反很厉害.
P7364 有标号二分图计数
$n$ 个点的二分图, $n\le 10^5$
考虑第一反应是枚举左半边, 然后枚举连边:
$$
f_n=\sum_i \binom{n}{i}2^{i(n-i)}\
\sum_i \dfrac{n! }{i! (n-i)! }2^2\cdot 2^{n-i}
$$
这个可以随便卷卷算.
但注意到这个不完全正确: 对于有 $x$ 个连通块的二分图, 因为你这么二染色, 会有 $2^x$ 种.
那么设刚才求的这个生成函数是 $F$, 连通二分图的为 $H$, 答案为 $G$.
容易发现 $e^{2H}=F$ 和 $e^H=G$, 于是实际上就对 $F$ 开根.
[ABC290F] Maximum Diameter
对于一个长度为 $n$ 的正整数序列 $X=(X_1, X_2, \cdots, X_n)$, 定义 $f(X)$ 为:
- 对于所有节点数量为 $n$, 且点 $i$ 的度数恰好为 $X_i$ 的树, 其直径的最大值. 如不存在, 则值为 $0$.
你需要对于所有长度为 $n$ 的正整数序列 $X$ 计算 $f(X)$ 的和, 可以证明其为有限值. 答案对 $998244353$ 取模.
$T$ 组数据. $1\le T\le2\times10^5$, $2\le n\le10^6$.
看到杜赢做这个题.
考虑对于某个整数序列, 让直径最长一定是串一条链, 然后把多出来的一度点直接挂在链上的点.
因此对于 $a_n$, 答案是 $\sum_i [a_i>1]$
考虑枚举一个一度点的个数 $k$, 答案是
$$
\sum_k (n-k+1)\binom{n}{k}\binom{n-2}{n-k-1}
$$
然后用范德蒙德卷积就可以化简完了.
P4709 信息传递
给定置换
$$
f = \begin{pmatrix} 1 & 2 & . . . & n \\ a_1 & a_2 & . . . & a_n \end{pmatrix}
$$
求有多少个置换 $g$ , 满足
$$
g ^ n = f
$$
答案对 $998244353$ 取模.$n \le {10} ^ 5$.
考虑拆环, 对于单个环考虑, 对于一个数 $i$, 乘上一个数就相当于在环上走一步 $i\to p_i\to p_{p_i}\ldots$.
那么, 若走 $x$ 步, 环长为 $l$, 环会变成 $gcd(x, l)$ 个小环, 按照膜 $gcd(x, l)$ 分类
于是你可以对着 $f$, 考虑有 $a$ 个环能拼成 $g$ 中的一个环, 条件是长度均为 $k$, 满足 $gcd(ak, n)=a$.
然后显然每个长度的环互不影响, 就能做了, 对于所有长度为 $k$ 的环, 设 $f_i$ 表示使用 $i$ 个的方案数, 钦定用 $a$ 个环拼起来时以第一个环第一个数为首, 又因为每个环地位相等, 所以用 $\binom{i-1}{a-1}$
$$
f_i=\sum_a [gcd(ak, n)=a]\binom{i-1}{a-1}f_{i-a} k^{a-1}k!
$$
[SDOI2017]序列计数
Alice 想要得到一个长度为 $n$ 的序列, 序列中的数都是不超过 $m$ 的正整数, 而且这 $n$ 个数的和是 $p$ 的倍数.
Alice 还希望, 这 $n$ 个数中, 至少有一个数是质数.
Alice 想知道, 有多少个序列满足她的要求.
$1\leq n \leq 10^9, 1\leq m \leq 2\times 10^7, 1\leq p\leq 100$.
观察数据范围, 考虑 $f_{i, j, 0/1}$ 表示前 $i$ 个数, 和膜 $p$ 余 $j$, 是否选了质数的方案数.
看到至少一个, 想到全都不是, 发现全都不是的只要做的时候只考虑非素数求就行了, 所以去掉 $0/1$ 维.
那么矩阵快速幂优化上面那个即可. 容易发现转移固定.
P6694 强迫症
给定圆上 $n$ 个点, 有点权 $a_i$, 将它连成一张图, 使得边不在非端点处相交, 边 $u\to v$ 的权值为 $a_u\cdot a_v$, 求期望权值和.
$n\le 10^5$
考虑方案数是好求的: 设 $n$ 个点方案数为 $f_n$, 钦定一号点连向编号最小的边为 $1\to i$, 则 $f_n=f_{n-1}+\dfrac{1}{2}\sum_i f_{i-1}\cdot f_{n-i}$, 直接卷.
那么考虑一条边 $u\to v, u<v$ 的贡献是 $a_u a_v f_{v-u+1}f_{n-(v-u+1)}/4$(除4是除必须选 $u\to v$).
还需要进一步优化, 注意到两个 $f$ 可以合成一个 $h_{v-u+1}$, 然后它和 $a_u$ 可以先卷出一个关于 $v$ 的东西, 就能行了.
P5363 [SDOI2019]移动金币
Alice和Bob将要进行如下的一场游戏. 二人轮流操作, 且Alice先行.
当轮到一个玩家的时候, 他可以选择一枚金币, 并将其向左移动任意多格, 且至少移动一格.
金币不能被移出棋盘, 也不能越过其它金币.一个 $1\times n$ 的棋盘上最初摆放有 $m$ 枚金币. 其中每一枚金币占据了一个独立的格子, 任意一个格子内最多只有一枚金币.
如果轮到一个玩家的时候他已经无法做出任何有效操作了(显然这个时候 $m$ 枚金币恰好落在最左侧的 $m$ 个格子中), 则被判定为输家. 已经知道Alice和Bob都是极致聪明的人, 他们在任何局面下总能做出最优的操作. 那么有多少初始状态能保证Alice必胜呢?
$m\le 50, n\le 150000$
发现不会判定.
学到了一个叫阶梯博弈的东西.
[trick] 说的是考虑有 $n$ 堆石子, 每次可以把第 $i$ 堆的移动到第 $i-1$ 堆, (规则为把第 $i$ 堆移动到左边任意一堆的同理), 那么实际上相当于一个仅考虑奇数堆的普通NIM游戏. 具体可以考虑, 如果对方移动一个偶数堆到奇数堆, 你立刻把它再往下移动到偶数堆, 这个操作一定可以进行且对奇数堆情况没有改变且不导致先后手变化, 相当于没干, 所以只要考虑一次把一个奇数堆移动没了就行了.
于是这个题, 把两个金币之间的距离当做石子堆, 问的就是有多少个序列 $a_m$, $\sum a_m<n$, 且 $\mathrm{xor}_{i=2k+1}{a_i\ne 0}$
这个东西同时要求 和 与 异或和, 看起来不是二进制多项式可以解决的.
考虑逐位考虑, 考虑只考虑奇数位上的数, 每位有偶数个 $1$, 层层之间无关, 对于每一层, 枚举选几个 $1$ 方案数得到一个 $a_i$ 表示和为 $i$ 的方案数, 卷起来就是总方案数.
最后再卷上偶数位上的方案数即可.
哦, 发现模数上智障的 $10^9+9$.
注意到奇数堆每一层最多选 $m/2$ 个盘子, 所以暴力卷复杂度是 $nm\log n$. 最后卷偶数堆的时候求的是后缀和, 也可以做到线性.
P3228 [HNOI2013]数列
求有多少个序列 $a_k$ 满足 $a_i-a_{i-1}\in [1, m], a_k\le n$
保证 $m(k-1)<n$
$n, k, m\le 10^9$.
显然式子是
$$
\sum_{i}^{n-1} (n-i) x^i^{k-1}
$$
关键在于 $m(k-1)<n$, 说明把多项式所有项都提取了.
那么问题变得清新: 多项式代入 $x=1$ 就是系数和, 而对于 $x^i\to ix^i$ 只需要求个导代入(展开带)
那么就是 $nm^{k-1}-(k-1)m^{k-2}\cdot m(1+m)/2$
CF960G Bandit Blues
给你三个正整数 $n$, $a$, $b$, 定义 $A$ 为一个排列中是前缀最大值的数的个数, 定义 $B$ 为一个排列中是后缀最大值的数的个数, 求长度为 $n$ 的排列中满足 $A = a$ 且 $B = b$ 的排列个数. $n \le 10^5$, 答案对 $998244353$ 取模.
当设 $f_{i, a, b}$ 表示 $i$ 个数, $a$ 个前缀max, $b$ 个后缀max时, 会有
$$
f_{n, a, b}=\sum_{i=1}^n f_{i-1, a-1, any} f_{n-i, any, b-1} \binom{n-1}{i-1}
$$
于是你的状态就只有两维, 设 $f_{i, j}$ 表示 $i$ 个数, $j$ 个前缀max即可.
又注意到, 考虑往后追加一个数这个数的排名, 易得 $f_{i, j}=f_{i-1, j-1}+(i-1)f_{i-1, j}$, 这是第一类斯特林数.
此时暴力应该是把两个求两个斯特林列然后卷起来. 为了好看
考虑组合意义, 它就是你从 $n-1$ 个数选 $i-1$ 个排成 $a-1$ 个环, 剩下的排成 $b-1$ 个环. 等价于从 $n-1$ 个数排成 $a+b-2$ 个环, 再从这里面选出 $a-1$ 个环.
所以 $f_{n, a, b}={n-1 \brack a+b-2}\binom{a+b-2}{a-1}$
P6144 [USACO20FEB]Help Yourself P
计算给定线段集(大小为 $n$)的所有子集并的连通块数目的 $k$ 次方的和对 $10^9+7$ 取模.
变量范围:
- $1 \leq n \leq 10^5$
- $2 \leq k \leq 10$
- $1 \leq l_i \lt r_i \leq 2n$, 且任意两个端点都不在同一位置上.
处理次幂的常见套路是组合意义和生成函数?
生成函数的话, 注意到 $e^{x+y}=e^xe^y$, 但 $\dfrac{1}{1-x-y}$ 不怎么好, 所以用EGF.
于是 $f_i$ 表示线段集合最右端在 $i$ 上的方案数EGF, 考虑插入线段 $[l, r]$ 后带来的影响:
- 对于 $i<r$, $f_i$ 没有影响
- 对于 $f_r$:
- $f_i, i<l$ 部分多了一条不交线段, $f_r : = f_r + e^x(\sum f_i)$
- $f_i, i\in[l, r]$ 部分相交的连通块数不变: $f_r : = f_r+\sum f_i$
- 对于 $i\ge [l, r]$, 不知道右边的左端点, 但如果按照 $l$ 从小到大考虑线段, 就一定所有情况都相交(且包含), 选不选没关系, 所以 $f_i: =2f_i$
要求区间多项式和, 区间多项式乘2, 单点修改, 可以上个线段树. 而乘法暴力卷积就行了. 复杂度是 $nk^2+nk\log n$
P7483 50 年后的我们
给出了 $n$ 个点, 每个点有一个权值 $c_i$ 和坐标值 $d_i$.
另外还有 $m$ 条线段, 第 $i$ 条线段的两个端点分别为 $l_i$ 和 $r_i$, 表示该线段覆盖了从 $l_i$ 到 $r_i$ 之间的所有点, 线段 $i$ 有 $p_i$ 几率被选中.
定义权值给出为所有点中, 至少被一条选中的线段覆盖的点的权值之和的 $k$ 次幂. $0^0=1$
求出权值的期望膜 $998244353$
$1\leq n\leq 400, 0\leq k\leq 400, 1\leq m\leq 10^5, 1\leq d_i\leq 10^9, 1\leq l_i\leq r_i\leq 10^9, 0\leq c_i, p_i<998244353$.
类比上一题处理次幂.
设 $f_i$ 表示 $i$ 为右端点的EGF. 插入一条线段 $[l, r]$ 时:
- $i<r$: $f_i: =(1-p)f_i$
- $r$: $f_r: =(f_r+p\sum_{i\in [l, r)} f_i)\cdot e^{\sum c_i}$($[l, r]$ 中的 $f$ 转移过来再卷上所有被包含的点)
- $i>r$: 无影响
要区间乘一个东西, 区间多项式和, 还有暴力卷积, 复杂度是 $nk^2+nk\log n$ 吧
「SiR-1」Bracket
给定仅有
(,)的括号序列 $s_n$, 求 $\sum_{l<r} f(S_{l, r})$, 其中 $f(S)$ 表示, 可以进行任意循环移位 和 任意添加一个左或右括号 的情况下使得 $S$ 是匹配括号串的最小次数. $n\le 2\times 10^7$
对于固定的 $S$ 考虑 $f$ 如何求.
首先括号个数肯定要对, 调完之后此时前缀和就是 $0$ 了, 容易想到Raney定理说你最多只会进行一次循环移位.
再考虑什么时候需要循环移位, 仍然考虑前缀和折线, 众所周知加括号一定加在最前或最后, 设前缀和数组为 $a$, 那么发现加完括号不用再操作当且仅当: $\forall i, a_i\ge 0$ 或 $a_n=\min_i a_i$, 画画图还是很显然的.
那么开始数数, 先不考虑循环移位, 那就是数 $\sum_{l
然后数不用再操作的个数, 两个条件同时满足当且仅当已经是合法序列, 那么这个是好数的, 接下来对于同一个 $l$, 可以直接二分出满足 $a_i\ge 0$ 条件的区间, 对于同一个 $r$ 可以直接二分出自己作为最小值的区间, 总复杂度1log.
单调栈可以线性啊, 拉了.
群友题
对于序列 $a_n$, 求有序对 $(i, j, k)$ 个数满足 $i<j<k, 2a_j=a_i+a_k$. $n, a_i\le 10^5$
对序列分块, 枚举 $j$, 其中 $i, k$ 与 $j$ 在同一块的直接用桶处理掉, 不在同一块的考虑fft即可.
P2012 拯救世界2
求有多少个长 $n$ 序列满足 $\texttt{a, b, c, d}$ 出现任意次, $\texttt{e, f, g, h}$ 出现奇数次, $\texttt{i, j, k, l}$ 出现偶数次.
$n\le 2^63$, 多次询问
以前只知道egf:
- $\texttt{a, b, c, d}$: $e^x$
- $\texttt{e, f, g, h}$: $\dfrac{1}{2}(e^x+e^{-x})$
- $\texttt{i, j, k, l}$: $\dfrac{1}{2}(e^x-e^{-x})$
全都卷起来提取系数即可.
另一种做法是直接矩阵乘法优化dp, 设 $f_{i, j}$ 表示前 $i$ 位, 后 $8$ 种字符中有 $j$ 种出现奇数次, 用矩阵乘法优化dp.
[AGC008E] Next or Nextnext
给定正整数 $n$ 和一个长度为 $n$ 的序列 $a$, 问有多少长度为 $n$ 的排列 $p$, 满足对于任意 $i$ 有 $p_i=a_i$ 或 $p_{p_i}=a_i$.
答案对 $10^9+7$ 取模.
$n \leq 10^5$.
见到排列还有这个 $p_{p_i}$ 直接拆环考虑. 一开始读错题以为 $a$ 也是排列, 那显然 $p$ 中的环在 $a$ 中也是一个环, 对于单独一个环, 方案数是 $1+(n\bmod 2)$, 两个大小相同的环可以合并, 方案变为 $len$. 这个数起来就, 对每个大小的环分别考虑, 相当于算从 $n$ 个中选 $k$ 个匹配的方案数, 可以简单组合数.
然后要考虑 $a$ 组成的图中的基环树, 也是好做的, 容易发现一个基环树无法和环合并, 树上每个点除了环边最多有一个入度, 看起来像是把一堆链的链头串起来. 那么因为无法合并每个基环树单独做, 对于一个基环树上的一个点 $i$ 在环外有长为 $l$ 的链, 如果 $i$ 在环上往前走 $l$ 个点都没挂链方案数是 $1$, 如果往前 $l+1$ 个都没挂链方案数是 $2$, 否则是 $0$, 于是就做完了.
ARC134F Flipping Coins
给定一排 $n$ 枚硬币, 初始时所有硬币正面向上.
Snuke 会等概率地选择一个长度为 $n$ 的排列 $p = (p_1, p_2, \dots, p_n)$, 并执行 $n$ 次操作. 第 $i$ 次操作会执行如下步骤:
- 若第 $i$ 枚硬币是反面朝上的, 什么也不做.
- 若第 $i$ 枚硬币是正面朝上的, 翻转它, 并翻转第 $p_i$ 枚硬币.
给定 $w$. 设 $n$ 次操作完后正面朝上的硬币数为 $k$, 则这排列的贡献即为 $w^k$.
你需要求出这贡献的期望值乘 $n!$ 后在模 $998244353$ 意义下的值. 容易证明这值定是整数.
$1\le n\le 2\times 10^5, \ 1\le w < 998244353$.
考虑排列拆成若干个环独立, 那么可以算一个环的答案然后 exp. 再考虑对于一个环可以分成若干个递增段, 则硬币 $i$ 当且仅当一个递增段最后一位 $p_j=i$ 且递增段长度为奇数才会是正面.
于是一个递增段的贡献关于长度的生成函数可以写成 $F(x)=\sum_{i=0} w^{i\bmod 2}\dfrac{x^i}{i! }$. 但是环的EGF并不是 $G(x)=\sum_{i=1} \dfrac{F^i}{i}=\ln 1-F$ 因为不满足连续段极长的限制, 也就是实际上的一个连续段由多个卷起来的连续段贡献了.
考虑容斥, 对于每个长 $i$ 的连续段给系数 $c_i$, 则一个方案的容斥系数是 $\prod c_i$, 总答案是 $\sum \prod_{i\in S} c_i$, 这里 $S$ 是遍历不加限制的拼的方案. 如果一个段实际上的值是 $a_i$, 那么总的答案 $\sum \prod_{i\in T} a_i$, 这里 $T$ 是有极长限制的拼法的情况, 那么若对于一段 $a_i$ 是所有拼出它的系数的和 $a_i=\sum c_j$, $\sum \prod_{i\in T}a_i$ 就真的等于 $\sum \prod_i (\sum c_j)$ 了. 所以只要满足一段的容斥系数是对的, 也就是这一段的真实权值 $a_n=\sum_{S_k\ s. t. \ \sum_i s_i=n} \prod_i c_{S_i}$, 其中 $S$ 是每一种拼出长 $k$ 连续段的方案数. 翻译成生成函数, 设 $H(x)=\sum_{i=0} w^{i\bmod 2}x^i$, 则 $\dfrac{1}{1-C(x)}=H(x), \therefore\ C(x)=1-\dfrac{1}{H(x)}$.
刚才得到的 $C$ 是 $c_i$ 的OGF, 换成EGF $C_e=\sum_i c_i\dfrac{x^i}{i! }$ 就可以带到刚才 $G$ 的错误式子里得到答案了, $Ans=\exp G(x)=\exp (\ln (1-C’))=1-C’=(\dfrac{1}{H(x)})_e$. (用 $F_e$ 表示 $F$ 对应的EGF).
最后你只要求逆再求逆.
LOJ6728 U群把妹王 TopCoder13444
有 $n \times m$ 个格子, 每个格进行染色, 可以选择 $k$ 种颜色之一. 对于集合 $S, T$, 你需要计数有多少种格子的染色方案, 满足:
- 对于每一行的图案拿出来, 和它相同的图案总共有 $r$ 行 (含自身), 则 $r \in S$.
- 对于每一列的图案拿出来, 和它相同的图案总共有 $c$ 列 (含自身), 则 $c \in T$.
答案对 $P = 998244353$ 取模.
为了让这道题看起来代码比较健康, 保证 $1 \in S \cap T$.TopCoder是这个的 $S=T={1}$ 情况
虽然先看的这个题, 但感觉上面的ARC134F里对这个容斥说的更清楚.
首先弱化版是斯特林数反演题, 考虑如果只要求列互不相同方案数是 $f(n)={(k^n)}^{\underline{m}}$, 而 $g(n)$ 表示在此基础上要求行互不相同, 那么有 $f(n)=\sum_i {n\brace i}g(i)$, 于是直接反演得到 $g$ 即可.
强化版考虑更强的容斥, 对于一维问题每种颜色出现次数必须在 $S$ 中, 不考虑限制, 方案数是 $k^n$, $k^n$ 意味着有些相同, 把相同的元素组成的集合再放到一起组成集合 $L={S_1\ldots S_l}$, 其中每个 $S$ 表示一个颜色相同的集合, 那么最后答案应该是 $\sum_L c(L)k^{\vert L\vert}$, 现在因为限制是对 $\vert S_i\vert$ 的, 我们希望 $c(L)=\prod_i d(\vert S_i\vert)$, 这样一来取 $k=1$ 就有
$$
ans(n)=[x^n]1+\sum_{i\in S} x^i=\sum_L c(L)=n! [x^n]\exp(\sum_i \dfrac{d(i)x^i}{i! })
$$
所以 $d$ 的egf就是 $\ln 1+F$, 其中 $F=\sum_{i\in S}x^i$.
那么二维情况下, 容斥系数可以直接相乘, 让 $f_i$ 表示 $\vert L\vert$ 为 $i$ 的方案的容斥系数之和, $g$ 为另一维的, 发现答案为 $\sum_i \sum_j f_ig_ik^{ij}$, 而 $k^{ij}=k^{\binom{i+j}{2}-\binom{i}{2}-\binom{j}{2}}$, 于是只要卷一下, 所以问题来到求 $f$.
而又由定义, $f_i=n! [x^n] \dfrac{\ln^i (1+F)}{i! }$, 新建一个元 $u$, 则 $f$ 是 $[x^n] \exp(u\ln(1+F))$ 这个复合函数求某项系数可以拉反:
$$
[x^n]\exp(u\ln(1+F))=\dfrac{1}{n}[x^{n-1}]ue^{ux}(\dfrac{x}{G(x)})^n
$$
这里 $G$ 是 $\ln(1+F)$ 的复合逆, 可以牛迭. , 复杂度 $\vert S\vert n\log n$
P3349 ZJOI2016 小星星
给定一张无向图和一棵树, 求有多少种点集到点集的双射使得若两点在树上有边则图上对应的两点也有边.
$n\le 17$
考虑dp, 从树的结构出发肯定比图好, 设 $f_{u, i, S}$ 表示 $x$ 映射到 $i$, 子树中的点映射过去组成的集合是 $S$ 的方案数. 转移显然, 复杂度 $n^33^n$ 或子集卷积后 $n^42^n$ 爆炸.
考虑 容斥掉排列限制的trick(见南外省选集训>ICPC模拟赛2>F. Non-Puzzle: The Lost Array), 然后就可以不记录 $S$, 复杂度是 $n^32^n$
[AGC041F] Histogram Rooks
给一个底端对其, 第 $i$ 列有 $h_i$ 个格子的网格, 求有多少种填车的方案使得每个位置都能被至少一个车攻击到.
$h_i\le n\le 400$
容斥, 钦定选了 $c$ 个不能被覆盖的格子, 则容斥系数是 $(-1)^c$, 但这样没法走了, 考虑钦定存在未被覆盖格子的列的集合 $S$, 容斥系数还是 $(-1)^{\text{未覆盖格子数}}$, 那么现在一个长 $l$ 的行连续段如果经过 $k$ 个 $S$ 中的列, 要么这 $k$ 个位置都不是钦定的, 贡献 $2^{l-k}$, 否则枚举这 $k$ 个位置中有 $i$ 个被钦定, 则贡献 $\sum_{i=1}^k \binom{k}{i}(-1)^i=-[p>0]$.
但这样不能保证一开始说的 $S$ 中的列都至少有一个格子被覆盖, 但注意到现在的限制对象从格子变成了列, 问题已经得到简化, 再容斥, 设集合 $T$ 中的列中不能有被选的, 容斥系数是 $(-1)^{\vert T\vert}$, 那么仍然考虑刚才长 $l$ 的段, 经过 $k$ 个 $S$ 中元素其中有 $j$ 个 $T$ 中的没有被钦定不能覆盖的格子, 那么贡献就变成了 $2^{l-k}$ 和 $-[k>j]$(为什么不是 $2^{l-k+p}$? 发现第一类贡献其实不会算错, 要消去的是第二类的错误贡献)
然后考虑dp, 前面那个网格很容易让人想搞笛卡尔树dp, 设 $f_{u, i, 0/1}$ 表示当前在笛卡尔树上的 $u$ 点, $u$ 经过了 $i$ 个 $S$ 中的格子, 以及 $k$ 是否等于 $j$(如果某个点开始 $k>j$, 则其祖先必然 $k>j$, 所以只要记这个信息就够了). 复杂度是树形背包的 $n^2$.
P5405 [CTS2019] 氪金手游
题意概要: 给定 $n$ 个点, 点 $w_i$ 分别有 $p_{i, 1}$, $p_{i, 2}$, $p_{i, 3}$ 的概率取 $\frac{1}{2/3}$.
**在确定了所有的 $w_i$ 后再开始游戏:**不断抽点, 点 $i$ 被抽中的概率为 $\frac{\sum w_j}{\sum w_j}, j=1 \text{ to } n$, 直到所有点都被抽中过.
给定 $n-1$ 个二元组 $(u, v)$ 表示第一次抽中 $u$ 的时间需要比第一次抽中 $v$ 的时间早, 且若将这 $n-1$ 个二元组中的两个元素连无向边, 则这张图是一棵树.
问满足所有二元组限制的概率. $n\le 1000$
第一眼以为树一定是外向, 也就是限定了拓扑序, 那么根节点一定是子树中的点中第一个被选的, 忽略子树外的点是概率没有影响, 那么设 $f_{u, i}$ 表示子树 $u$ 内部权值和为 $i$ 的概率即可吧.
然后发现有些边方向不对, 那就容斥掉, 钦点一条反向边不考虑/一定违反, 带着系数dp即可.

