dp选做

省选dp挂了不会来补一补

刷题记录-2022暑假前

UVA1626 括号序列 [dp] [区间dp]

区间dp(似乎括号类的都是区间dp? )

设 $f_{l, r}$ 表示把区间l到r中补到合法的操作步数, 则转移是:

最外侧是匹配的括号: $f_{l, r}=f_{l+1, r-1}\ \ s. t. \ s_l=s_r$
区间由若干 $f_{l, r}=\min_{l\le k\le r}{f_{l, k}+f_{k+1, r} }$
在最右侧添加一个与最左侧的括号匹配的括号或相反, 发现这种情况不优于直接在与这个新添加的括号匹配的括号旁边直接匹配

然后初始情况就是 $f_{i, i}=2$ , 表示为每个括号加一个反括号匹配

这题输出方案, 所以记录最有解位置即可.

P1220 关路灯 [dp] [区间dp]

由于老王走过去关一盏灯时顺手关掉路上经过的一定不劣, 所以被关掉的灯是一个区间, 于是记 $f_{l, r}$ 表示已经被关了的灯的区间, 发现这样转移不了, 比如当我们向右扩展一位时我们不知道老王是刚刚关完左端点的灯还是右端点的, 所以设 $f_{l, r, 0/1}$ 表示区间 $[l, r]$ 已经关掉, 老王此时正在左端点或右端点转移即可.

UVA1362 Exploring Pyramids [dp] [区间dp] [计数dp]

每个子树对应欧拉序上一段区间, 可以区间dp统计答案

设 $f_{l, r}$ 表示 $[l, r]$ 这段区间的方案数, 转移就是枚举第一棵子树划分到哪里, 即

$$
f_{l, r}=f_{l+1, k-1}*f_{k+1, r-1}\ s. t. \ s_k=s_l=s_r\ \mathrm{and}\ k\in[l+2, r-2]
$$

$s$ 为颜色区间, 因为 $l$ , $r$ , $k$ 对应的都是根的颜色.

P7914 [CSP-S 2021] 括号序列 [dp] [区间dp] [计数dp]

仍然区间dp

$f_{i, j}$ 表示区间 $[i, j]$ 的方案数, 则转移就是同UVA1626最外层相等的情况和中间划分的情况, 但这题要求方案数, 发现对于中间划分时, 形如”()()()”的括号既可以划分成”()+()()”也可以划分成”()()+()”, 会被计算多次, 所以设 $g_{l, r}$ 表示 $l$ 和 $r$ 恰好匹配的情况, 转移就成了 $f_{l, r}=g_{l, k}*f_{k+1, r}$ , 然后考虑亿点点细节.

P5504 [JSOI2011] 柠檬 [dp] [斜率优化]

首先显然相当于把序列划分成若干段的方案

重要结论是对于划分的每一段, 两端点贝壳大小相同, 否则把它划分到其他部分或单独成段一定不劣.

所以我们可以只考虑相同颜色的转移, 令 $f_i$ 表示考虑前i个的答案, $cnt_i$ 表示第i个贝壳的大小包含它的前缀中的出现次数, $size_i$ 表示它的大小, 则转移可以枚举前面的j, 就是

$$
\begin{aligned}
f_i&=f_{j-1}+size_i\times(cnt_i-cnt_j+1)^2\\
&=f_{j-1}+size_i\times cnt_i^2+size_i\times cnt_j^2+size_i\\
&\ \ \ \ -2size_i\times cnt_i\times cnt_j - 2size_i\times cnt_j+2size_i\times cnt_i\\
\end{aligned}\\
$$

发现可以斜率优化, 所以整理式子:

$$
\begin{aligned}
(2size_i\times cnt_i)\times (cnt_j) \\
+(f_i-size_i\times cnt_i^2-size_i-2size_i\times cnt_i) \\
=f_{j-1}+size_j\times cnt_j^2-2size_j\times cnt_j
\end{aligned}\\
$$

这里用到刚才结论 $size_i=size_j$ , 式子中的四个括号分别是直线的 $k$ , $x$ , $b$ , $y$ .

注意式子对颜色不相同的情况是不成立且不保证答案更小的, 所以要对每种颜色单独维护凸包. 右发现对于同种颜色, $cnt_j$ 和 $2size_i\times cnt_j$ 单调增, 所以用单调栈维护上凸壳即可.

[trick] 先分类再每一类分别进行斜率优化的dp

P3515 [POI2011]Lightning Conductor [dp] [决策单调性]

每个点 $i$ 对后面的贡献函数是 $\sqrt x$ 的平移, 发现一旦一个决策点的答案到另一个之上, 另一个再也没有机会反超, 所以这个题满足决策单调性.

于是有几种可以的方法利用决策单调性:

分治法: 设当前区间为 $[l, r]$ , 可能的决策在 $[pl, pr]$ , 每次扫一遍算出序列上mid的答案, 则 $[l, mid-1]$ 中决策点在 $[pl, p]$ 中 $[mid+1, r]$ 中决策点在 $[p, pr]$ 中, 可以递归处理
单调队列或栈, 此题为单调队列: 用容器存储三元组 $(l, r, p)$ 表示以p为最有决策点的区间为 $[l, r]$ , 每次加入一个节点时, 如果它最后也不优秀就不用管, 否则二分出它和队尾的决策点切换的分界点 $k$ , 即它在 $[k, n]$ 更优秀而队尾在 $[l, k]$ 更优秀, 把原本队尾的区间修改并把它push进去
SMAWK: to do ~~等我先学会了~~

分治法适用于离线决策单调性, 即 $f_i$ 的计算不依赖 $f_{[1, n]}$ 的答案, 而单调队列或栈的方法适用于可以快速计算在某个决策点下的答案的情况.

这种相同凸函数的平移, 常常存在决策单调性, 还有常见的 $y=\max{(a(x-b), c)}$ 和 $y=ax^2+bx+c$ , 其中要求所有a均相同, b单调(不单调可能也行? )

P2497 基站建设, P4655 Build Bridges [斜率优化] [dp] [李超树] [cdq分治]

方程过于模板了不放了.

推出方程后可以斜率优化, 没什么单调性所以用李超树或cdq或平衡树或二进制分组维护斜率优化dp, 基站建设注意第一步要初中几何一下.

P4027 [NOI2007] 货币兑换 [dp] [斜率优化] [李超树] [cdq分治]

设 $f_i$ 表示第i天能拥有多少钱(在把所有券都卖光的情况), 转移就是考虑它能卖的券是之前的哪一天买的, 但这题给的比较麻烦, 首先要做一些转换, 设 $a_i, b_i, c_i, d_i, r_i$ 分别为两种券的钱数, 两种券的数量和题目中的 $Rate_i$ , 列出方程:

$$
\begin{cases}
a_ic_i+b_id_i=f_i\\
\frac {c_i} {d_i}=r_i
\end{cases}
$$

解出来得到:

$$
\begin{cases}
c_i=\frac{f_ir_i}{r_ia_i+b_i}\\
d_i=\frac{f_i}{r_ia_i+b_i}
\end{cases}
$$

于是方程就是:

$$
\begin{aligned}
f_i&=c_ja_i+d_jb_i\\
\frac {f_i}{b_i}&=c_j\frac {a_i}{b_i}+d_j\\
\end{aligned}
$$

现在就已经是斜率优化的形式了, 对于这种没有单调性的题目, 常见做法是cdq, 李超树和平衡树维护, 个人感觉李超树是最简单好用的. 复杂度 $O(n \log n)$

实现细节: 注意这里李超线段树的下标域是 $[1, 10]$ 的有理数, 可以先把所有 $\frac {a}{b}$ 离散化, 加速并不用卡精度.

HDU4991 Ordered Subsequence [dp] [线段树] [树状数组]

真正的线段树树状数组优化dp模板, 然而我是先做的后面那个基站选址, 但它更模板所以被我放到前面

首先暴力式子应该还挺显然的, 设 $f_{i, j}$ 表示以第 $i$ 个结尾, 长度为 $j$ 的LIS长度, 式子就是

$$
f_{i, j}=\sum_{k < i, a_k < a_i} {f_{k, j-1} }
$$

初始条件 $f_{i, 1}=1$

然后和基站选址类似的是它的 $m$ 最大100, 可以承受 $O(nm\log n)$ , 所以把j改为在外层枚举, 考虑优化式子

$$
f_i=\sum_{k < i, a_k < a_i} f_k
$$

然后就是简单二维数点求和, 这里可以线段树也可以离散化后树状数组上

P2605 基站选址 [dp] [线段树]

首先要推出暴力dp式子, 设 $f_{i, j}$ 表示考虑前i个村庄, 在第i个村庄建了第j个基站的花费, 这里不考虑i到n部分的赔偿, 记 $i$ 到 $j$ 部分的补偿为 $cost(i, j)$ , 第i个村庄建立基站的花费为 $c_i$ , 则转移就是看上一个基站在哪:

$$
f_{i, j}=\min_l {f_{l, j-1}+cost(l, i)} + c_i
$$

暴力转移为 $O(n^2k)$ , 发现这里n很大而j不大, 所以可以只优化i的转移, 外层暴力枚举j, 另外发现式子只和 $j-1$ 有关, 可以滚动掉一维空间, 式子就成了

$$
f_{i}=\min_l {f_{k}+cost(k, i)} + c_i
$$

困难在于计算 $cost(k, i)$ , 正向计算在 $f_i$ 时哪些村庄在选 $k$ 时要赔偿较为困难, 可以反过来想对于每个村庄选择那些 $k$ 需要时需要赔偿这个村庄, 首先可以预处理对于每个村庄向左右最远到哪里建设不需要赔偿, 分别记为 $l_k$ , $r_k$ , 则对于一个村庄, 仅当处理到的 $i>r_k$ 且选择的 $k < l_k$ 时需要赔偿, 所以可以数据结构维护 $f_{k}+cost(k, i)$ , 则转移时就是查询 $[1, i-1]$ 的区间最小值, 每次处理完 $i$ 后, 对于所有 ${r_i=l_k}$ 的村庄, 如果k在 $[1, r_i]$ 中需要赔偿, 所以给这个区间加上它的赔偿费用, 由于是区间加, 区间最小值, 可以使用线段树完成

第一次做线段树优化dp, 所以开始找其他类似题目. . .

CF675E Trains and Statistic [dp] [贪心] [RMQ]

然后发现被骗了, 这题并不需要线段树优化dp, 因为这就一个RMQ根本不用线段树. . .

首先发现如果我们能到达 $i$ , 则一定能到达任意 $j s. t. \ j < i$ , 因为我们可以在任意时刻中途下车

由于上面的性质, 可以对每个i找出 $\max_j{a_j}\ s. t. j\in[i, a_i]$ , 这个 $j$ 的意义是如果我们要走的这次到不了, 那么应该走到 $j$ , 记它为 $next_i$
这个可以用静态RMQ直接求, 我觉得猫树最可爱容易理解而好用

要求的这个答案应该可以想到计算对于每一个i的 $\sum_j {\mathrm{dis}(i, j)}$ , 记为 $f_i$ , 要想办法求 $f_i$ , 你可以画出下面的示意图

-------------------------------------------
       -------------------
                                   -------
       ^                  ^       ^       ^
       i                nxt[i]  a[i]      n

发现对于 $f_i$ 相比 $f_{nxt_i}$ 有两段距离增加, 一段是 $[i+1, nxt_i]$ , 是原来不需要走的, 另一段是 $[a_i+1, n]$ , 需要先用一步走到 $nxt[i]$ 再继续走, 所以转移为

$$
f_i=f_{nxt_i} + (n - a_i) + (nxt_i - i)
$$

倒序递推即可

CF946G Almost Increasing Array [dp] [树状数组]

我认为这个也不是严格的线段树优化dp, 它只是在值域上树状数组维护最大值而已

首先套路的可以把每个数减去他们的下标, 把问题转化为非严格递增, 这样转化的好处是, 我们可以任意在两个数中间添加一个值, 而原来如果这两个数相邻我们不能添加小数.

然后可以反向思考能留下哪些, 发现留下的就是已有的非严格LIS, 所以我们要在可以删一个数的前提下求这个LIS

思考删除这个数造成哪些影响, 发现对于它后面的每个数, 删去它后下标前进了一个, 也就是变大了一个

于是在原有LIS的dp上进行修改, 设 $f_{i, 0/1}$ 表示考虑前i个, 是否已经删除过一个数, 则转移有三种:

尚未删除任何数: $f_{i, 0}=\max {f_{j, 0} } + 1, \ s. t. \ j < i, a_j\le a_i$
已经删除过一个数: $f_{i, 1}=\max {f_{j, 1} } + 1, \ s. t. \ j < i, a_j\le a_i$
现在正要删一个数, 仍然考虑子序列里上一个数是谁, 因为这个与上一个间删除了一个数, 所以这个数的值变大了1, 所以式子为 $f_{i, 1}=\max {f_{j, 0} } + 1, \ s. t. \ j < i, a_j\le a_i+1$

然后用树状数组记录值域上前缀max即可

CF739E Gosha is hunting [dp] [wqs二分] [二维wqs二分] [费用流]

这题可以从费用流考虑, 从源点连到左边一排点表示宝可梦, 边权为2, 费用为0, 从宝可梦连向右边两个点表示两种球, 这一步边权为1, 费用为用这个球能捉住的概率, 从右边的球向汇点连边, 容量 inf , 边权为0, 但是发现同时对一个宝可梦使用两种球时还要减去两个同时发生的概率(独立事件), 所以把源点到宝可梦的每条边拆成两个, 一个容量为1边权为0, 另一个容量为1边权为两概率相乘, 就有了一个费用流做法, 已经可以通过.

有了费用流能说明关于流量(使用球总个数)有凸性, 所以可以进行二分一种球的使用数量把朴素的 $O(n^3)$ dp优化成 $O(n^2)$ 的, 然后又可以二分另一种的优化成 $O(n \log^2 n)$ 的, 可以更稳通过此题

然而这个题直接这么两重wqs二分是假的, 一重wqs二分时有两种写法, 分别找到:

最大的斜率满足使用球数小于要求的
最小的斜率满足使用球数大于要求的

这两个的选择要和二分时的 check 函数相对应, 比如题目 P4694 Raper 中有些买光盘决策收益为0, 这类光盘如果不购买则使用个数较少, 购买则个数较多, 分别对应前面两种情况, 所以二分时是要有这种对应的, 而当拓展到二维时, 就需要我们找到两者都最少的, 这里以谁为第一关键字似乎是个问题. 目前有两种解法:

给每个数再加一个很小的随机权值, 直接避免出现这类二分遇到直线和平面的情况
二分过程中mid不再等于l+r, 而是等于两者之间的一个随机位置, 这个样跑一次成功概率较小, 需要重复多次选一个答案最小的(来自机房大佬qyc), 注意这种方法保证正确性的同时会TLE并不能通过

所以还是很玄, 我再思考能不能在dp决策过程中使某个最小但仍然很困难. 有人有好办法了告诉我.

P2619 Tree I [wqs二分] [最小生成树]

是时候来点清新WQS二分了

凸性的证明是困难的(目前还没看到), 先尽量感性理解, 就是考虑总边数一定的情况下, 使用白边少时会需要用一些不优点黑边顶上, 多时要必须选一些不优的白边, 说明它是有一个谷的. . . 然后就不会了

在通过打表, 瞎猜等方式得到凸性之后就很简单了, 二分给每个白色边加上一个权值C(给所有黑色边也是一样), 再按照新的权值跑Kruskal, 统计有多少条白边去调整二分区间即可.

P4983 忘情 [wqs二分] [斜率优化]

中规中矩的wqs二分

首先把给的式子拆开后发现~~npy很善良~~其实就是 $(sum+1)^2$ , 那么不考虑段数情况下就是简单斜率优化, 考虑段数的情况就再使用wqs二分, 给每一段一个附加代价二分

这个题凸性证明由qyc给出, 先考虑原始dp方程, 即 $f_{i, j}$ 表示前 $i$ 个划分 $j$ 段, 则有

$$
f_{i, j}=\min(f_{k, j-1}+(sum_i-sum_k)^2)
$$

对于类似 $f_{i, j}=\min(f_{k, j-1}+w(k, i))$ 这种方程, 或者更泛化一些,对于在一个 DAG 上走k步从1走到n的最短路问题, 如果边权满足四边形不等式, 那么答案是关于k的凸函数

然后再把sum变成前缀和形式拆开, 平方也拆开, 就有了一个显然斜率优化, 其中k和x都是单增多, 单调队列即可

几个关于决策单调性/凸性结论

wqs二分实现难点

为了统一, 把wqs二分中二分的值为 $C$ , 通过二分改变的题目要求的值为 $K$ , 答案为 $A$

问题主要是二分时二分区间变化的选择要与check函数相对应, 比如如果check函数选择的是给定 $C$ 下 $K$ 最小的, 那么二分时就应二分最大的小于等于 $K$ 的, 否则如果是给定 $C$ 下 $K$ 最大的, 则二分最小的大于等于 $K$ 的, 是一个十分重要的细节, 例子:

Tree I中, 出现黑色白色边权值相同时, 如果选择白色边, 则相当于选择 $K$ 最小的, 我们要二分出最大的小于 $K$ 的
忘情中, 对于斜率优化中是否取等, 不取等相当于选择 $K$ 最小的, 要二分出最大都满足条件段数的
Gosha is hunting中, 对于遇到使用不使用球期望相同的情况, 选择不使用相当于 $K$ 最小, 要二分最大的球数小于 $K$ 的
Raper中对于获益为0的光盘是否要买也是相同的

凸性证明

费用流问题, 费用是关于流量的凸函数
忘情中写的对于在一个 DAG 上走k步从1走到n的最短路问题, 如果边权满足四边形不等式, 那么答案是关于k的凸函数
打表出奇迹
四边形不等式的一个思考方式, 首先只要证明 $f(l, r)+f(l-1, r+1)$ 与 $f(l-1, r)+f(l, r+1)$ 的关系, 其次一个常用方法是, 因为问题常常是每个位置有一个贡献, 这个贡献和区间的其他位置有关(而不是直接跟区间), 那就仅考虑 $l-1$ 位置从区间 $[l-1, r+1]$ 移动到 $[l, r]$ 的贡献

P4481 BJWC2018 序列合并 [dp] [区间dp]

qyc说这是他童年阴影题, 然而他只用了两分钟就秒了

首先它长的这么像石子合并, 让人想到一个区间dp, 于是一种做法是记 $f_{l, r}$ 表示区间 $[l, r]$ 合并成一个的代价, 转移时就相当于要把这一段划分成k段, 所以可以用一个 $O(n^3)$ 的dp, 然后会得到一个五次方TLE做法

然后简单想一下发现对每个l向右跑一遍就能得到所有的r, 就成了四次方, 卡卡常就过了

不过还有一种长的更像区间dp的理解, 设 $f_{l, r, k}$ 表示把区间 $[l, r]$ 合并成k段, $g_{l, r}$ 表示这一段合并成一段的答案, 则方程就是

$$
\begin{aligned}
f_{l, r, k}&=g_{l, p}+f_{p+1, r, k-1} \ s. t. \ , k\ge 2 \
g_{l, r}&=\min f_{l, r, k} \ s. t. \ k \in [L, R] \
f_{l, r, 1}&=g_{l, r}
\end{aligned}
$$

P4767 邮局

[结论] : 对于一个区间中的一个邮局, 若区间长度为奇数则邮局建在中位数上, 偶数则建在中间两个数的任意一个上~~小学奥数经典~~

于是就可以考虑把原序列分成 $P$ 个区间, 每个区间里放一个邮局, 所以设 $f_{i, j}$ 表示前 $i$ 个村庄分了 $j$ 段(也就是建了 $j$ 个邮局)的代价, 转移即

$$
f_{i, j}=\min f_{k, j-1}+cost(k+1, i)
$$

其中 $cost(l, r)$ 表示在区间 $[l, r]$ 中建立一个邮局的最小代价, 这个代价可以 $n^2$ 递推, 但我认为这种方法更好: 考虑知道中位数后, 距离就是对中位数两边的位置一一匹配后匹配位置间距离的和, 如图:

示意图

可以结合图理解, 蓝色点表示村庄, 红色即表示一对位置的匹配, 总代价就是所有匹配点之间距离的和, 也就是右边的每个点位置分别减去左边每个点位置之和, 可以先处理一个前缀和之后 $O(1)$ , 用这个式子去做复杂度就成了 $O(n^2p)$ , 由于奇数偶数时的差异, 式子是

$$
cost(l, r)=(sum_r-sum_{\lfloor \frac {l+r}{2} \rfloor})-(sum_{\lfloor \frac {l+r-1}{2} \rfloor}-sum_{l-1})
$$

接下来遍历能进行的优化策略, 式子有与 $k$ , $i$ 均有关的项废掉了单调队列, 这个项里与 $i$ , $k$ 相关的东西在下标里废掉了斜率优化, 只剩下wqs二分和决策单调性, 由于我在上面wqs二分总结的结论, 问题就转化为证明 $cost$ 满足四边形不等式

抛开式子会发现包含单调性的显然, 在原有区间上增加新村庄代价一定不会降低

对于四边形不等式的证明复杂一些, 首先因为 $x$ 单调递增, 所以 $sum$ 是凸函数, 此外在证明 $cost_{l, r}+cost_{l+1, r-1}\ge cost_{l+1, r}+cost_{l, r-1}$ 时会消掉所有 $sum_r$ 和 $sum_{l-1}$ , 剩下的可以套用琴生不等式证明

这样同时证明了四边形不等式和凸性, 单用四边形不等式可达到 $n^2$ 通过, 使用 wqs 二分和决策单调性可以达到 $n \log n\log v$

汪娟的一套dp题

[BJOI2019]光线

若干层玻璃叠在一起, 一束光照到玻璃上时会有 $\dfrac{a}{100}$ 的光透过而 $\dfrac{b}{100}$ 的光反射. 不保证 $a+b=100$ 求从一边射入1, 从另一边射出多少.
$n\le t\times 10^5$

$f_{i, 0/1, 0/1}$ 表示第 $i$ 个玻璃从前/后方向射进去光从前/后出来的大小是进去的多少倍即可.

[SCOI2009]粉刷匠

$n$ 条木板, 每条有 $m$ 个格子, 要被涂成0/1, 每次只能选择一个木板上连续的一段涂成0/1, 每个格子只能被涂一次, 只能粉刷 $t$ 次, 求能对多少.
$n, m\le 50, t\le 2500$

考虑一条木板上的情况, 显然设 $f_{i, j}$ 表示前 $i$ 个涂了 $j$ 次的最多个数即可.

那么现在有多条木板, 做一个泛化背包合并即可. 复杂度 $nm^2$ 之类的

P1373 小a和uim之大逃离

$n\times m$ 的网格, 每个格子上有一个数, 从任意格子开始任意格子结束, 每次向右或向下走一步. 手上有两个数初始都为 $0$ , 站在走到的第奇数个格子时(包括开始和结束格子)让第一个数加上网格上的数, 否则让第二个数加上. 每次加上之后都与 $k+1$ 取模. 求由多少种方案结束的时候两个数相同.
$n, m\le 800, k\le 15$ .

如果从 $(1, 1)$ 起点是简单的, 设 $f_{i, j, k, l}$ 表示走到 $(i, j)$ 左右手分别是 $k$ , $l$ 的方案数, 复杂度 $n^2k^2$ .

可以进一步优化, 由于我们只关心是否相同, 可以用emiya家今天的饭的方法只记录差, 去掉一个 $k$

从任意位置结束只要求所有位置的dp值累加, 从任意位置开始只要每个位置转移的时候都额外算上这个位置的. 同时注意因为起始位置不同还要记录一维 $0/1$ 表示这一步加给哪个数.

CFdp乱做

是选择通过人数降序, 难度2600, 标签dp.

带有combination/greedy的可能没有, 被收录到数数/贪心中.

CF1431G

给一个 $n$ 个数的集合, 每轮A选一个不是最大值的数删掉, 然后B选一个比A选的大的数删掉, 并给得分累加两数的差, A希望最大得分, B希望最小得分, 求最后得分.

$n\le 400, k\le \lfloor \dfrac{n}{2} \rfloor$

首先发现, 任意情况B选的一定是A选的后继, 只要B按照这个选就一定是最小的, 即使 $[1, 2, 3, 4]$ 中A选 $2$ , B选 $3$ 后下一次强制 $1$ 和 $4$ 也不比 $(3-1)+ (4-2)$ 更劣, 于是B的方案就是确定了. 所以实际上选出的是若干连续段, 对于一个连续段 $[l, l+2x-1]$ , 其得分为 $\sum_{i=l}^{l+x-1}+ a_i-\sum_{i=l+x}^{l+2x-1} a_i$

接下来就考虑A要如何选, 考虑dp, 设 $f_{i, j}$ 表示前 $i$ 个元素中, 两人选了 $2j$ 个数的情况下的得分, 转移是这个数不选或枚举最后选的一段, 复杂度 $nk^2$

注意这题只能Kotlin交哦.

CF1740F Conditional Mix

给定 $n$ 个数, 每次可以把两个不交集合并起来, 求任意次合并后集合大小组成的可重集的方案数. 膜998244353.

$n\le 2000$

值排序, 从小往大扫的好处是对不用考虑交.

$f_{i, j}$ 表示前 $i$ 个值, 组成 $j$ 个集合, 加入这一层的时候可以选择新开若干层或者加到已有的里面去. 但是 $S$ 只关心大小就死了.

考虑一个多重集 $S$ 合法当且仅当其和为 $n$ 并且降序排列时 $\sum_{i\in[1, k]} S_i\le \sum_{i\in [1, n]} \min(k, cnt_i)$ . $cnt_i$ 为数 $i$ 的出现次数.

感觉必要性比较显然(前 $k$ 个集合最多每个选 $1\ldots n$ 各一个), 充分性就直接体会把可以合并的拆开肯定是没问题的.

于是直接dp, 设 $f_{i, sum, last}$ 表示选了前 $i$ 个, 总和是 $sum$ , 最后一个是 $last$ 的即可. 复杂度 $n^3$ .

进一步分析, 考虑 $n\ge last\times i$ , 于是 $last$ 的取值是自然对数, 总复杂度就是 $n^2\log n$ 了.

[trick] 数数dp考虑最终合法判定

CF321E Ciel and Gondolas

给定 $a_n$ , 要求你把它分成 $k$ 组, 若 $a_i$ 和 $a_j$ 分为一组会产生 $w_{i, j}$ 的代价, 最小化代价和.

$n\le 4000, k\le 800, w_{i, j}\ge 0$

看一看发现是简单题, 显然 $cost(l, r)$ 是满足四边形不等式, 直接分治就结束了.

CF631E Product Sum

给定序列 $a_n$ , 移动一个数最大化 $\sum i\times a_i$

$n\le 2\times 10^5$

可以先假定是往后移动, 再反过来做一遍即可.

考虑 $f_i$ 表示从某个位置插入到 $i$ 后面的答案最大值, 那么就是

$$
\max_j suf_{i+1}+pre_{i}-a_j j+a_j(i+1)+sum_i-sum_j
$$

直接斜率优化.

CF662C Binary Table

给定 $n\times m$ 01矩阵, 每次选择一行或一列翻转01, 求翻转任意次后1的个数的最小值.

$n\le 20, m\le 10^5$

对每一种行的是否翻转情况, 列是否翻转是确定的. 只是不能直接计算.

猜到是FWT, 但不会. 做法是, 设 $a_i$ 表示 $i$ 这种状态的出现次数, $b_i$ 表示二进制数 $i$ 的0/1个数的较小值, 那么当行的状态为 $S$ 的时候答案就是

$$
f_S=\sum_T a_T\cdot b_{T\mathrm{xor}S}\
f_{S \mathrm{xor} T}=a_S\cdot b_T
$$

于是直接FWT-XOR即可.

CF1208F Bits And Pieces

给定 $d_n$ , 求 $i<j<k$ 最大化 $d_i\mathrm{or}(d_j\mathrm{and}d_k)$

$n\le 10^6$

又是FWT.

考虑从高到低贪心, 那么要确定是否有三个数这样运算起来包含一个前缀.

先解决后两个的与运算, 做一遍高维后缀和得到包含每个位置下标的最大值, 次大值即可.

然后再解决或, 做一遍高维前缀和得到每个位置被贡献的最小位置即可.

然后就简单贪心.

CF1344C Quantifier Question

给定 $n$ 个变量 $x_n$ 和 $m$ 个关系, $m$ 个关系每个形如 $x_i<> x_j$ , 求序列 $q_n, q_i\in{\exists, \forall}$ , 使得拼出来 $q_i x_i$ 满足这 $m$ 个关系. 求最大的任意的个数和一个 $q$ 的方案, 或判断无解

我天什么烂题面, 举个例子:

假设 $n=2, m=1$ , 关系是 $x_1<x_2$ , 那么可以 $\forall x_1, \exists x_2, x_1<x_2$ , 不能 $\exists x_1, \forall x_2, x_1<x_2$ 或两个都是 $\forall$ , 所以最大个数是1.

$n, m\le 2\times 10^5$

考虑建一个图, 若要求 $x_1<x_2$ 则 $x_1\to x_2$ , 如果有环肯定无解, 注意到序列维和图上都是有意义的. 考虑若 $i<j$ 且 $x_i\to x_j$ , 那么显然 $x_j$ 不能是任意, 如果有 $i<j$ 且 $x_j\to x_i$ 同理, 于是一个点可以选当且仅当没有一个在它之前的点与它连通. 注意到有向图所以不能直接搞连通块, 而是类似dp的做法: $f_u$ 表示能走到 $u$ 的最小的, 那么 $f_u=\min { u, \min f_v}\ s. t. \ v\to u$ 即可. 反着也是类似.

CF6D. Lizards and Basements 2

给定序列 $a_n$ , 每次可以选定 $i\in (1, n)$ , 对 $a_i$ 减去 $c_1$ , 对相邻的两个减去 $c_2$ , 问几次全小于0.

$n\le 10, 1\le c_2<c_1\le 10, a_i\le 15$

不是, 为啥数据范围有点小啊?

显然顺序无所谓, 于是 $f_{i, j}$ 表示前 $i$ 个位置, 第 $i+1$ 个位置减去了 $j$ 的代价, 那么转移到 $f_{i+1, k}$ 的时候只要枚举 $i+1$ 上被减了几下即可. 但这个是不对的, 发现可能干 $i+1$ 的时候 $i$ 死了, 所以再多记一维即可.

CF750E New Year and Old Subsequence

给定 $a_n$ , $q$ 次询问给定区间 $l, r$ , 删去最少的使得其没有子序列 $\texttt{2016}$ 而有子序列 $\texttt{2017}$

$n\le 2\times 10^5$

画出识别2016, 2017的自动机

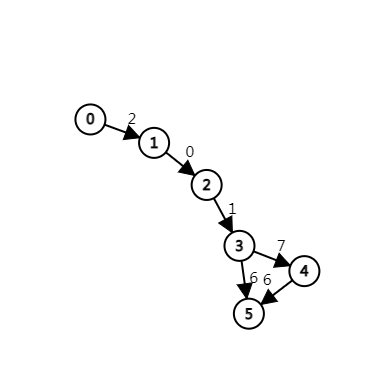
然后设 $f_{i, j}$ 表示前 $i$ 个自负, 走到节点 $j$ 至少要删多少, 用静态ddp做就好了.

CF1363F Rotating Substrings

给定 $s_n, t_n$ , 每次可以选择 $s_{l\ldots r}\to s_{r, l, l+1, \ldots r-1}$ , 求最少次数让两者相等.

$n\le 2000$

把循环移位操作看成插入, 就不考虑除了 $r$ 以外字符的影响了.

于是 $f_{i, j}$ 表示前 $i$ 个字符相等, 已经插入 $j$ 个字符的最小代价, 那么现在让 $i$ 这一位相等, 发现根本不会. 因为后面可能有若干字符跑到前面去, $s_{1 \ldots i}$ 不会和 $t_{1\ldots i}$ 相等, 所以改为 $f_{i, j}$ 表示 $s_{1\ldots i}=t_{1\ldots j}$ 的最小代价.

可能的转移包括:

$s_i=t_j$ , $f_{i, j}=f_{i-1, j-1}$
$s_i$ 需要被插入到前面去, $f_{i, j}=f_{i-1, j}+1$
$s_i$ 从后面被插入过来, $f_{i, j}=f_{i, j-1}$

取个 $\min$ 即可.

CF650D Zip-line

给定 $a_n$ 和 $m$ 个操作 $x_i, v_i$ , 表示把 $x_i$ 改成 $v_i$ , 对每个操作求出操作后的LIS, 操作独立.

$n, m\le 4\times 10^5$

是修改一次后的LIS. LIS分为不跨过 $i$ 的, 当前包含 $i$ 的, 将来包含 $i$ 的三种, 第一种显然直接解决.

考虑当前包含 $i$ 的影响, 只要求出 $f_i$ 和 $g_i$ 分别表示 $i$ 往前, 往后的LIS长度. 删掉 $i$ 就是 $f_i+g_i-1$ .

最后一种是将来包含 $i$ 的, 新的 $f_i, g_i$ 的dp值就是直接矩形数点, 就做完了.

CF1554E You

给定 $T=Tree(n)$ , 生成 $a_n$ 的过程是每次选择一个未被标记的点 $u$ , $a_u$ 为与 $u$ 相邻的点未被标记的个数, 然后将它标记, 求 $T$ 生成的排列中 $\gcd=k$ 的数量

膜 $998244353$ , $n\le 10^5$

本质是给边定向, $a_u$ 是点 $u$ 的入度.

那么任意两种不同定向方式 $a_u$ 是否可能相同? 你感觉一下发现只有有环才有可能, 所以合法的 $a$ 到定向方式是双射.

考虑若 $a$ 可以得到, 一定要满足 $\sum a_i=n-1, a_i<d_i$ , 显然不充分.

不会凑, 那只好从树上看定向方式, 设 $f_{u, v, 0/1}$ 表示子树内和 $u$ 的父边所有定向方式中, 父边朝外/内形成的 $gcd$ 为 $v$ 的方案数, 每次转移考虑父边的方向. 似乎是可以的. $u$ 取值范围只有 $\log$ . 转移的时候就先合并子树内的方案, $g_{i, j}$ 表示 $u$ 度数为 $i$ , 当前 $gcd$ 为 $j$ 的方案数, 加入一个子树时是gcd卷积, 最后复杂度应该是 $n\log n\log\log n$ 吧.

看题解, 原来 $k>1$ 的的时候方案最大是1, $k=1$ 的时候减去大于1的

考虑如何判定大于1的即可, 首先所有叶子边都是内向(不能有入度是1), 然后叶子全删了到下一层, 这样每次定向叶子即可. 原来我才是智障啊.

CF755F PolandBall and Gifts

给定 $p_n$ , 点 $u$ 是好的当且仅当点 $u$ 不是坏的且 $p_v=u$ 的点 $v$ 也不是坏的, 现在已知有 $k$ 个点是坏的, 求此时最少/最多有多少点不是好的.

$n\le 10^6$

看到排列想形成了若干环.

考虑根据这个定义一个点坏了其实是坏了它和它连向的点, 所以是每次干掉一条边, 求答案.

那么对于最大值, 一定要先让它每次干掉两个点, 最后干长奇数的环剩下的一个点即可. 对于最小值, 最好的方式显然是干满若干环, 这样平均每次干都是1的贡献.

于是最大值可以直接统计奇环个数, 最小值要找若干环加起来是 $k$, 所以就成了多重背包.

$10^6$ 卷起来上过不了了, 但显然不同的环长只有根号个, 就多重背包直接结束了.

CF258D Little Elephant and Broken Sorting

给定排列 $p_n$ , $m$ 次操作交换 $p_i, p_j$ , 每一个操作有0. 5概率执行, 求逆序对期望.

$n, m\le 1000$

交换和逆序对没有简单关系, 因为 $n\le 1000$ 考虑拆贡献.

于是求每一对数 $i, j, p_i<p_j$ 的概率. 设这个为 $f_{i, j}$

初始状态应该是 $f_{i, j}=[p_i>p_j]$ . 每次进来一个操作 $a, b$ , 考虑:

$$
f_{i, a}=\dfrac{1}{2}f_{i, a}+\dfrac{1}{2}f_{i, b}
f_{a, b}=f_{b, a}=\dfrac{1}{2}
$$

最后求个和就做完了.

CF1223F Stack Exterminable Arrays

对于一个序列, 定义其可消除当且仅当从头开始扫它, 若栈顶等于当前元素就弹, 否则就入栈, 最后栈是空的.

给定 $a_n$ , 求有多少子区间是可消除的.

$n\le 3\times 10^5$

从前往后扫, 一个序列可以消除当且仅当其第一个元素入栈前和最后一个元素出栈后栈相等.

直接hash变成求相等元素对数.

就是dwtoj 括号序列加强版

CF1389F Bicolored Segments

给定 $n$ 条线段 $[l_i, r_i]$ , 每个线段有颜色 $t_i\in {1, 2}$ , 要选择最多的线段满足没有两个颜色不同的线段有交集(包括包含)

$n\le 2\times 10^5$

考虑结束时, 一定是若干段颜色相同的, 之间没有交.

于是设 $f_{i, 0/1}$ 表示前 $i$ 个位置, 最后一段是 $0/1$ , 就要找 $f_{k, 0/1}+w(k, i)$ 最大, 然后发现是线段树优化dp, 移动到一条线的右端点就区间加即可.

CF1566F Points Movement

数轴上有 $n$ 个点 $a_i$ , $m$ 个区间 $[l_i, r_i]$ , 你可以任意次花费1的代价将一个点向左向右移动1, 求保证每个区间都有过某个时刻含有至少一个点的最小代价.

$n\le 2\times 10^5, \vert a_i\vert, \vert l_i\vert, \vert r_i\vert \le 10^9$

读错题了.

那么先删掉显然多余的区间(已经有点的, 包含另一区间的). 可以把区间, 点排序.

于是现在是若干段点和区间, 每个点一定只会折返一次并且不会跨过起点.

于是现在每个点走过包含自己的一个区间. 如果一个点跑过一段区间编号 $[i, j]$ , 那么一定是走过 $[r_i, l_j]$ , 代价是 $r_i-l_j+\min(x-r_i, x-l_j)$ .

于是考虑dp: $f_{i, j}$ 表示前 $i$ 个点干掉了前 $j$ 个区间的最小代价, 注意状态数线性因为每个点的区间不会越过相邻点, 于是只要考虑转移, 现在的情况是

$$
f_{i, j}=f_{i-1, k}+cost(k+1, j, i)
$$

其中 $cost(x, y, z)=(r_y-l_x)+\min (r_y-p_z, l_x-p_z), (y<z)$ 那因为都是一次项在没有 $min$ 的时候可以直接优化, 有的话就对 $min$ 两边分别维护即可.

CF797F Mice and Holes

$n$ 个老鼠, $m$ 个洞, 告诉你他们的一维坐标和 $m$ 个洞的容量限制, 问最小总距离.
$n, m\le 5000$

模拟费用流!

(我感觉这题网络流直接冲)

可以dp. $f_{i, j}$ 表示前 $i$ 个老鼠, 进前 $j$ 个洞的最小总距离, 转移可以枚举这个洞装了几个老鼠, $f_{i, j}=f_{k, j-1}+cost(k+1, i, j)$ , $cost$ 是区间中的点到另一个点的最小距离, 直接前缀和, 于是单调队列优化, 于是做完了.

CF813D Two Melodies

给定 $a_n$ , 求找两个不交子序列使得长度和最大, 要求子序列满足相邻两个元素差为 $1$ 或膜 $7$ 同余.

$n\le 5000$

一个子序列很显然, 两个子序列设两维, $f_{i, j}$ 表示第一个子序列选到 $i$ , 第二个选到 $j$ . 因为影响一个序列后面能不能选的只有最后一个元素所以我们是正确的.

CF917D Stranger Tree

给定 $T=Tree(n)$ , 对每个 $k\in [0, n-1]$ , 求有多少 $T’=Tree(n)$ 与 $T$ 有恰好 $k$ 条边相同. 相同指边的两个顶点相同.

$n\le 100$

见到这种是不是应该立刻容斥, 钦定 $k$ 条边相同, 于是现在有 $n-k$ 个连通块, exCaylay说你要算 $\sum \prod siz$ , 注意选完这 $k$ 条边的连通块一定是树上的连通块, 所以就 $f_{i, j, k}$ 表示子树 $i$ 内选了 $j$ 个连通块, 连到 $i$ 上的这个里有 $k$ 个点. 复杂度 $n^4$ .

然后发现组合意义: $\prod siz$ 相当于每个连通块选一个点, 于是第三维改成 $0/1$ 表示是否已经选过, $j$ 一维合并的时候用树上背包的办法, 复杂度就 $n^2$ .

CF1051E Vasya and Big Integers

Vasya 有三个大数字 $a, l, r$ . 求把 $a$ 划分成连续的若干段使得每一段的数字大小在区间 $[l, r]$ 之内(注意是按照数字大小比较而非按字符串大小比较), 且不含前导零的方案总数. 由于答案可能很大, 只需输出答案对 $998244353$ 取模的结果.

$n\le 10^6$

首先地球人都知道的dp是 $f_{i}$ 表示前 $i$ 个, 想了想你觉得设后 $i$ 个更好, 此时满足条件的 $i$ 一定是一个区间.

那不就直接做了, 每次满足条件的一个区间, 区间长度与 $l, r$ 不同的可以直接搞掉, 现在还剩下判断相等的怎么弄, 可以二分/exkmp算一算lcp然后比较lcp的下一位即可.

CF441E Valera and Number

给定 $x$ , $k$ 次操作, 每次有 $p$ 概率乘 $2$ , 否则加 $1$ , 问最终 $x$ 二进制末尾0个数的期望.
s
$x\le 10^9, k\le 200$

考虑这个是左移和加一.

发现加一的影响相对有点小. 感觉可以设最后8位表示的数是 $x$ 之类的, 但一个全1段就死了, 那再记录一个从最后8位开始的1长度是不是就行了, 现在状态成了 $f_{i, j, k, l}$ 表示 $i$ 次操作, 最后8位是 $j$ , 从最后8位往上有 $k$ 个0, $l$ 个1.

你想了想, 发现 $k$ 和 $l$ 有一个一定是0, 所以就解决战斗了吧.

可以去杜赢那里看另外两个做法.

CF576D Flights for Regular Customers

给定有向图 $Graph(n, m)$, 当走过至少 $d_i$ 条边后允许走第 $i$ 条边, 问 $1$ 到 $n$ 最短路
$n, m\le 150, d_i\le 10^9$

$n, m$ 很小而 $d$ 很大, 可以考虑邻接矩阵快速幂. 于是想到按 $d_i$ 排序, 不断加边. 用矩阵快速幂维护走 $k$ 次能到的位置并用bitset加速. 并且用每一次的位置集合跑多源bfs即可.

CF932F Escape Through Leaf

有一颗 $n$ 个节点的树(节点从 $1$ 到 $n$ 依次编号). 每个节点有两个权值, 第 $i$ 个节点的权值为 $a_i, b_i$.

你可以从一个节点跳到它的子树内任意一个节点上. 从节点 $x$ 跳到节点 $y$ 一次的花费为 $a_x\times b_y$. 跳跃多次走过一条路径的总费用为每次跳跃的费用之和. 请分别计算出每个节点到达树的每个叶子节点的费用中的最小值.

注意: 就算树的深度为 $1$, 根节点也不算做叶子节点. 另外, 不能从一个节点跳到它自己.

$2\leq n\leq 10^5$, $-10^5\leq a_i\leq 10^5$, $-10^5\leq b_i\leq 10^5$.

dp方程显然(设 $f_u$ 表示 $u$ 的答案, $f_u=\min_{v\in subtree(u)} f_v+a_u\cdot b_v$)

于是李超线段树合并优化dp看起来很好.

[trick] 李超树合并复杂度单log.

证明就是考虑每一个线最多被下传 $\log n$ 次.

CF1733E Conveyor

有一个 $120$ 行, $120$ 列的棋盘, 行列编号均为 $0, 1, \cdots, 119$, $i$ 行 $j$ 列的格子的坐标为 $(i, j)$, 左上角的格子坐标为 $(0, 0)$. 每一个格子上都有一个传送带, 初始方向为右.

一开始, 有一个史莱姆在 $(0, 0)$, 其他格子都什么也没有, 每一秒传送带的方向都会如下变化:

所有的史莱姆随着传送带的方向移动一格. 如果传送带的方向没有格子, 史莱姆就会离开棋盘; 如果两个史莱姆到了同一个格子上, 就会合并为一个史莱姆.

所有有史莱姆的传送带的方向都会改变, 向右的会变成向下的, 向下的会变成向右的.

$(0, 0)$ 处会出现一个史莱姆.

给定 $q$ 个询问, 问在第 $t$ 秒, $(x, y)$ 格是否有史莱姆.

显然两个史莱姆不可能碰上

显然一个格子的周期是 $2^{x+y-2}$, 但发现一个格子第一次到达的时间貌似没啥规律, 所以取模这套行不通了.

考虑一个好算的是前 $t$ 时刻内经过一个格子的次数, 可以 $n^2$ 递推(必然一半一半的到了下方和右方).

于是就做完了.

[trick] 把有没有前缀和成经过次数来做

POI Pizza delivery

给一棵 $n$ 点树, 有边权, 要求选至多 $k$ 条路径(可重复经过点和边), 使得每个点经过至少一次, 最小化路径经过的边权和(重复经过算多次).

$n, k\le 10^6$

显然每条路都停在叶子上.

朴素dp说 $f_{u, i, j}$ 表示有 $u$ 点进去 $i$ 条边出来 $j$ 条边.

但注意到, $j\le 1$, 因为你往一个 $u$ 里放好多条路径的目的就是让其中的路径不用出来, 如果有两条路径都要出来不如替换成一条路径.

又注意到, 如果 $j=1$ 则 $i=1$, 因为又出来的路径做了个环, 可以接在进去没出来的上面, 然后原来那条出来的路径删掉这个环.

于是 $f_{u, i}$ 表示 $u$ 个点, 其中有 $i$ 条边进入子树且没出来.

$$
f_{u, 0}=2 \cdot edgesum(u)\
f_{u, k}=wk+\min_{a_n} \sum_{v} f_{v, a_v}
$$

注意到, 叶子显然是凸的, 如果 $f_v$ 是凸的, 那么一次min-add卷积再加一个一次函数之后也是凸的(下凸).

而 $f_{u, 0}$ 按照上面的式子算比下面的多考虑了父边, 所以只会更大, 因此合并上去也是凸点.

于是wqs二分即可.

CF1461F Mathematical Expression

给一个长度为 $n(n\le 10^5)$ 的序列 $a$, $0 \le a_i\le 9$, 现在给定你可以用+, -, *, 中的集合 $S$ 中的符号填到序列中 $n-1$ 个位置上, 使得最后的式子运算结果最大, 乘法运算优先于加法与减法, 请输出最后的式子
$n\le 10^5$, $S\subseteq {+, -, *}$

考虑如果 $S$ 不包含 ${+, *}$, 那么这是智障题, 于是现在 $S$ 是 ${+, *}$

但此时不能直接一个斜率优化板子dp拍上去: 因为前缀积存不下.

分析性质, 注意到如果有 $0$ 直接拆成若干毫无关系的段, 对于每一个, 显然连续非 $1$ 段中间都是乘号, 问题来到了两段之间的 $1$(第一个段前面的 $1$ 当然都是加号).

注意到, 如果所有数乘起来不出意料的存不下, 那么一定中间全是乘号.

否则, 因为每个段至少是 $2$, 所以段数只有 $\log$ 段, 直接段数平方dp.

CF1511G Chips on a Board

Alice 和 Bob 有一个 $n\times m$ 的棋盘. 每行恰好有一个棋子.

他们以如下的方式进行一个游戏:

选择一对整数 $l, r(1\leq l\leq r\leq m)$, 将除第 $l\sim r$ 列之外的部分从棋盘上移除.

轮流进行操作, Alice 先手. 每一次操作, 玩家需要选择一个棋子, 并将其向左走任意正整数步(不能移出棋盘). 第一个不能移动的玩家判负.

给定 $q$ 次独立的询问如 $L_i, R_i$ 所示, 试求如果第一步中选择的整数是 $(L_i, R_i)$, 谁会赢得游戏.

$1\leq n, m, q\leq 2\times 10^5$.

如果不考虑那个区间, 博弈论部分当然不能更简单了: 就是每行坐标异或和.

于是现在就是求一个值域区间的所有数减左端点值的异或和.

一个众所周知的技巧是trie全局加减1, 那么在这个过程中维护异或和, 搭配一个莫队可以做到 $n\sqrt n\log n$. 卡常听说可过.

考虑假设左端点固定, 区间 $[l, l+2^{k-1}]$ 和 $[l+2^k, l+2^k+2^{k-1}]$ 的前 $k$ 位异或和是相同的, 并且第 $k$ 位只和后一个区间内的数的个数有关. 于是用这个倍增即可做到单log.

[2022SDFZ省选模拟赛1]石子游戏

Alice 和 Bob 在玩取石子的游戏.

他们共有 $N$ 堆石子, 第 $i$ 堆石子有 $a_i$ 个石子.

Alice 和 Bob 轮流取石子, Alice 先取, 每一次取石子, 当前取石子的人可以任选一堆还没有被取完的石子, 从中取出至少 $1$ 个, 至多 $x$ 个石子.

如果当前取石子的人没有石子堆可选, 那么他(她)就输掉了游戏. 他们想知道, 如果 Alice 和 Bob 都用最优策略玩游戏的话, 谁会胜利.

由于 Alice 和 Bob 还没商量好 $x$ 取多少, 所以对于每个 $1$ 到 $N$ 之间的 $x$, 你都需要告诉他们谁将取得胜利.

$N\le 5\times 10^5, a_i\le N$

类似上一题

CF1218C Jumping Transformers

你要从 $(0, 0)$ 向右或向下走到 $(N - 1, M - 1)$

图上有 $K$ 个障碍, 每个障碍有 $(t_i, e_i, d_i, x_i, y_i)$, 在 $t_i$ 时刻, $(x_i, y_i)$ 会出现一个障碍, 并且接下来的每秒会按照 $(x+d, y-d), (x+d, y), (x, y+d), (x, y)$ 的方式周期性移动(保证不会跳出边界). 恰好碰到这个障碍时, 你可以花费 $e_i$ 将它移除(以后都不出现). 问从起点到终点最小花费

$1 \le N, M \le 500$, $0 \le K \le 5 \times 10^5$, $d_i \ge 1$, $0 \le t \le N+M-2$

todo

CF1765C Card Guessing

有 $4$ 种花⾊的牌, 每种牌均为 $n$ 张, 则牌的排列⼀共有 $(4\cdot n)!$ 种.

现在你从牌堆中逐张地取出牌, 取牌之前你都会猜⼀下这张牌是什么花⾊. 你会根据之前的 $k$ 张牌中出现最少的花⾊来猜这张牌.

如果有多种花⾊都是最少的, 你随机地猜⼀种. 如果之前抽出的牌不⾜ $k$ 张, 就按之前的所有牌中的最少花⾊来猜.

问你猜对的期望次数是多少?

$n\le 500$

容易想到求某一次猜对的概率.

那么对于要考虑前 $k$ 张牌时, 方案数是

$$
\begin{gathered}
\binom{4n-k}{n-a, n-b, n-c, n-d}\binom{k}{a, b, c, d}\dfrac{n-\min(a, b, c, d)}{4n-k}\
=(a+b+c+d)! (4n-a-b-c-d-1)! \cdot \dfrac{(n-\min(a, b, c, d))}{a! b! c! d! (n-a)! (n-b)! (n-c)! (n-d)! }
\end{gathered}
$$

此时你枚举一个 $\min(a, b, c, d)$, 然后把序列 $i! (n-i)!$ 卷起来, 然后再乘上其他的那些只和 $a+b+c+d$, 也就是卷完的下标有关的东西就行了. 复杂度是 $n^3$(暴力卷)或 $n^2\log n$

CF1425B

给定一张 $n$ 个点 $m$ 条边的无向连通图, 保证无自环, 保证除节点 $1$ 外每个点的度数都为 $2$.

有两人 $\text{Red}$ 和 $\text{Blue}$ 同时从节点 $1$ 出发. 初始时所有边都是灰色. $\text{Red}$ 每经过一条边就会将它染成红色, $\text{Blue}$ 每经过一条边就会将它染成蓝色. 每轮中, 每人会选择一条与当前所在节点相连的、灰色的边, 并走到边的另一端. 同一轮里两人选择的边不能相同.

当无法进行下一轮时, 整个过程停止. 问两人能走出多少种不同的最终局面, 答案对 $10^9+7$ 取模. 两个最终局面不同当且仅当存在一条边, 在最终局面下颜色不同.

数据范围: $1\le n\le 2000$, $1\le m\le 2n$.

图的形状是一堆环, 有一个公共点1.

设环的大小序列为 $a$, 则一种方案对应集合划分 $S, T, {u} or \varnothing$, 使得 $S$ 中元素和与 $T$ 中和的差不多于 $a_u$

然后直接背包.

Luogu一个dp题单

P8321 『JROI-4』沈阳大街 2

给定 $a_n$, $b_n$, 求 $\dfrac{1}{n! }\sum_{p_n} \prod_i \min(a_i, b_{p_i})$
$n\le 5000$

考虑贡献由两个数中大的一个决定, 序列顺序是无所谓的, 实际上是寻找 $a$ 到 $b$ 的全匹配.

于是把 $a, b$ 放到一起, $f_{i, j}$ 表示前 $i$ 个数, 其中有 $j$ 个 $a$ 元素选择比它大的 $b$, 于是根据元素个数能算出 $b$ 选比自己大的 $a$ 的数量, 贡献都留到消去一个插头的时候算.

CF1628D2 Game on Sum (Hard Version)

Alice 和 Bob 正在玩一个游戏, 游戏分为 $n$ 个回合, Alice 和 Bob 要轮流对一个数 $x$ 进行操作, 已知这个数初始值是 $0$.

具体每个回合的行动规则如下:

Alice 选择一个在区间 $[0, k]$ 之间的实数 $t$.

Bob 可以选择让 $x$ 变成 $x+t$ 或者 $x-t$, 但是 Bob 在 $n$ 个回合之内至少选择 $m$ 次让 $x$ 变成 $x+t$.

Alice想让最终的 $x$ 最大, Bob 想让最终的 $x$ 最小.

已知双方均采用最优策略, 求最终的 $x$ 值(对 $10^9+7$ 取模).

数据范围保证: $1\le m\le n\le 10^6, k\le10^9+7$, $\sum\limits n\leq10^6$ .

考虑一个暴力, $f_{i, j}$ 表示用 $i$ 次, 其中减了 $j$ 次. 那么 $f_{i, j}=\max_c \min(f_{i-1, j}+c, f_{i-1, j-1}-c)$.

那么Alice应该会让内层全是 $\dfrac{f_{i-1, j}, f_{i-1, j-1}}{2}$. 边界大概是 $f_{i, 0}=ik, f_{0, i}=0$.

注意到没有 $\dfrac{1}{2}$ 再把 $k$ 变成 $1$ 就是组合数, 于是就做完了.

P8290 [省选联考 2022] 填树

有一棵 $n$ 个节点的无根树, 刚开始树上每个节点的权值均为 $0$. KK 想对这棵树进行一些修改, 他会任选一个节点作为初始的当前节点, 然后重复以下动作:

将当前节点 $i$ 的权值修改为一个正整数 $x$, 需满足 $l_i \leq x \leq r_i$. 其中 $l_i, r_i$ 是输入中给出的两个正整数.

结束修改过程, 或移动到一个与当前节点相邻的权值为 $0$ 的节点(如果不存在这样的节点, 则必须结束修改过程).

现在 KK 有两个问题:

在修改结束后, 可以得到多少棵不同的树, 满足树上非零权值的最大值和最小值的差小于等于 $K$? 其中 $K$ 是输入中给出的一个正整数.

这些满足条件的树的权值之和为多少? (树的权值定义为这棵树上所有节点的权值之和)

你需要输出这两个问题的答案模 $10^9 + 7$. 我们认为两棵树不同当且仅当至少存在一个节点的权值不同.

$n\le 200$

其实一年前看过一次了.

发现对于一个节点, 枚举一个最大值 $x$, 就能确定最小值的范围. 于是对于一个节点, 方案数是关于 $x$ 的 $5$ 段一次函数, 总和应该是 $5$ 段二次函数.

那么最后是 $5n$ 段的大约 $n$ 次函数, 考虑如何得到.

设 $f_u(x)$ 表示从 $u$ 出发向子树走的函数, $g_u(x)$ 表示 $u$ 以内的函数, $h_u$ 表示 $u$ 自己的函数. 树形背包合并这些分段函数.

对于子树 $u$, 其内的函数至高为 $siz$ 段 $siz$ 次, 合并应该是 $siz^2$ 的. 总复杂度是 $n^3$ 的.

笑死, 一直以为树上 $\sum siz^2$ 可以树卷积

然后你最后会求出一个多项式, 可以对着有限微积分把他做了.

不过更合理的是, 分析出 $n$ 段 $n$ 次的东西后, 直接刚才那个dp可以 $O(n)$ 算一次, 再配一个拉插就行了.

然后发现我dp的时候是个智障: 记录了 $f_{u, 0/1}, fh_{u, 0/1}$ 表示 $u$ 子树内有没有最大值的和 $u$ 子树内且由 $u$ 出发的路径中有没有最大值的, 但实际上可以去掉那一维容斥出来不好吗.

[AGC034E] Complete Compress

给你一颗 $n$ 个节点的树, 并用二进制串告诉你哪些节点上有棋子(恰好一颗).

可以进行若干次操作, 每次操作可以将两颗距离至少为 $2$ 的棋子向中间移动一步.

问能否通过若干次操作使得所有的棋子都在一个点上, 如果能, 输出最小操作次数, 如果不能, 输出 $-1$ .

$2 \leq n\leq 2000$.

考虑把最后所有节点都在的点当成根.

发现, 两个祖孙棋子向中间走是多余的. 于是每一步都让总距离减2, 步数变得确定.

那么设 $f_u$ 表示 $u$ 之内的点走到 $u$ 需要外面的点向上走几步, 那么转移的时候就是要解决, 给定一个数组, 每次给两个元素减 $1$, 求最后剩下的数最小. 暴力模拟的话, 每次是 $c\log c$($c$ 是儿子个数)(先排序, 然后不断用最大值和次大值匹配消掉).

注意到, 如果最大值不多于总和的一半, 那么一定可以消到 $sum\bmod 2$, 考虑消不掉一定是因为某一时刻最大值大于总和的一半, 而每次消最大值和次大值是不会发生这样的事情的.

于是可以直接转移了.

P4765 [CERC2014]The Imp

这道题的场景为你想要在商店里购买一件最值钱的魔法实体, 但是你只能携带一件, 每个魔法实体都锁在一个特殊的魔术宝箱中, 而宝箱的开启需要一定的金币, 同时小恶魔会用魔法将某一个魔术宝箱内的实体转化为毫无价值的灰尘(消耗你的金币), 你必须保留你已购买的魔法实体并离开商店. 你需要在小恶魔使用 $k$ 次灰尘魔法的前提下, 最大化你的收益(所购实体的价值减去购买所有实体和之前的灰尘的费用), 小恶魔则希望将这个收益最小化, 并且你和小恶魔都使用最佳策略.

$1\le n\le1. 5\times10^5, 0\le k\le9, 0\le v_i, c_i\le10^6$.

[trick] 一个确定性的(所有已经确定的信息公开, 不存在概率)问题, 可以看成双方决策透明, 可以按照你先提供你的所有可能方案, 然后它给你的每个方案给出它的策略, 在所有的里面选一个最小的.

需要注意到你的选择是 $v$ 从小到大的, 假设你选了一个大的, 再选一个小的, 发现无论恶魔在大的处打断, 还是小的处打断, 都是不优的.

于是你选了一个递增的序列, 而恶魔每次决定是否打断. 但是你并不会算打断后的贡献所以不会转移.

于是从后往前转移, $f_{i, j}$ 表示你最大的 $i$ 个中选, 其中恶魔用了 $j$ 次魔法的收益即可.

P4363 [九省联考 2018] 一双木棋 chess

两个人在 $n$ 行 $m$ 列的棋盘上下棋, 菲菲执黑棋先手, 牛牛执白棋后手. 落子规则是一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子. 每个格子上都写有两个非负整数 $a_{i, j}$ 和 $b_{i, j}$. 在游戏结束后, 菲菲的得分是所有有黑棋的格子上的 $a_{i, j}$ 之和, 牛牛的得分是所有有白棋的格子上的 $b_{i, j}$ 的和. 菲菲和牛牛都希望自己的得分减去对方的得分得到的结果最大. 问题是, 在给定的棋盘上, 如果双方都采用最优策略且知道对方会采用最优策略, 那么最终的结果如何.
$n, m\le 10$

尝试用chatgpt生成简化题意. 字确实少了100来个吧.

考虑我们只关心哪些格子可以落子. 状态数是要数一个阶梯数. 考虑差分就是 $0\ldots 10$ 中选10个数使和为10, 可以写一个搜, 发现原来这么少, 那么就随便做了.

[HNOI2007]梦幻岛宝珠

给你 $n$ 颗宝石, 每颗宝石都有重量 $w_i$ 和价值 $v_i$. 要你从这些宝石中选取一些宝石, 保证总重量不超过 $W$, 且总价值最大, 并输出最大的总价值.

$1\le n \le 100$, $1\le W, w_i, v_i \le 2^{30}$.

保证每个 $w_i$ 能写成 $a \times 2^b\space (a, b \in \mathbb N)$ 的形式, $a \leq 10$ , $b \leq 30$, 且答案不超过 $2^{30}$.

一个奇怪背包, 很经典.

因为看到那个保证, 所以按照 $b$ 分层处理.

于是 $f_{i, j}$ 表示 $2^i\times j$ 时的最大价值, 按照数位dp的思路从高位向低位做即可.

[AGC032D] Rotation Sort

给定一个排列 $p_n$, 你可以花费 $a$ 使一个区间最左边的数跑到最右边, 或者花费 $b$ 的代价使最右边到最左边, 求把整个序列变成升序的最少花费.
$n\le 5000$

每个数显然一次到位.

注意到不动的数是LIS, $f_{i, j}$ 表示前 $i$ 个数, 不动的数中最后一个是 $j$. 每次碰到一个新数, 比 $j$ 大可以固定, 或者往右走(从 $j$ 到 $i$ 这一段都被移动过, 一段往右的和一段往左的中间一定可以有一个不动的), 比 $j$ 小就往左走.

CF1626F A Random Code Problem

考虑期望线性性算每个 $a$ 自己的贡献, 那么 $f_{i, j}$ 表示选了前 $i$ 次, $a$ 已经被减去了 $j$, 此时的贡献. 复杂度是 $nk^3$

注意到, 如果两个数膜 $lcm(1\ldots 17)$ 相同, 转移是一样的, 可以一起处理, 只要dp的时候记录的是 $f_{i, j}$ 为一次函数表示贡献即可.

注意到, 膜17的余数没有用, 所以现在复杂度是 $lcm(1\ldots 16)k^3$

又考虑到, 你可以把所有数合起来一起dp, 记录 $f_{i, j}$ 表示当前数是 $i$, 还有 $j$ 轮要进行的贡献, 复杂度是 $720720k$

[AGC030F] Permutation and Minimum

有一个 $2 N$ 个数的序列 $A$, 从 $1$ 到 $2 N$ 标号. 你要把 $1 \sim 2 N$ 这些数填进去, 使它形成一个排列.

但是已经有一些位置强制填了特定的数了, 输入时会给出.

最后令长度为 $N$ 的序列 $B$ 为: 令 $B_i = \min{A_{2 i - 1}, A_{2 i}}$.

询问所有方案中能得到的不同的 $B$ 的数量.

$1 \le N \le 300$.

首先全是 $-1$ 的时候发现实际上看成选一条从 $(0, 0)$ 每次走 $(1, 1)$ 或 $(1, -1)$ 走到 $(n, 0)$ 的方案数再乘 $n!$, 因为显然此时只要考虑给数配对, 每一对数的 $\min$ 的集合, 于是从小到大, 让第 $i$ 次走 $(1, 1)$ 表示第 $i$ 小的数作为一个数对的 $\min$ 即可.

而现在有了一些确定的数, 显然填好的数对直接扔了, 而填了一半的是重点, 因为现在它的位置是重要的了! 那么只能考虑dp, 肯定是记录 $f_{i, j, k}$ 表示前 $i$ 个数, 有 $j$ 个填了一半且位置不定的和 $k$ 个填了一半且位置确定的. 如果从小到大走发现, 从大到小则很容易, 每次要么新开一个对要么结束一个以前的对, 如果用当前位置位置确定的结束一个不确定的对则要乘上不确定的个数, 相当于此时为那个对确定位置. 复杂度 $n^3$.

感觉比较迷惑的在于怎么看出转移方向, 主要问题就在于每个对中大的那一个不重, 于是从小到大dp时结束一个对的位置不同不应算多次, 但这个没法整.

其他

CF1768F Wonderful Jump

给定整数 $n$ 和长度为 $n$ 的序列 $a$.
从位置 $i$ 跳到位置 $j(1\leq i\leq j\leq n)$ 需要花费 $\min(a_i, a_{i+1}, \cdots, a_j)\times(j-i)^2$ 枚金币.
对于 $k=1, 2, \cdots, n$, 求出从位置 $1$ 经若干次跳跃后跳到位置 $k$ 需要的最小金币总数.
$n\le 4\times 10^5, a_i\le n$

考虑现在在 $i$ 要从 $j$ 转移, 区间最小值为 $m$.

容易发现的结论是, 如果 $m=a_j$, 你选择的一定是一个后缀min, 如果是 $a_i$ 就没什么规律.

不容易发现的结论是, 如果一步走过去优于每次走一格, 即 $i-j=l, l^2\min_k a_k<\sum a_k<nl\Rightarrow ml<n$

有了这个剩下就, 根号分治, 对于 $l>\sqrt n$ 的情况, 如果 $m=a_j$ 就维护单调栈, 元素显然少于 $\sqrt n$, 如果是 $a_i$, 直接暴力往前走到第一个 $a_j\le a_i$, 因为每个值只会最多覆盖整个序列一遍所以复杂度对的.

[trick] 存在两种可能操作, 可以看一种在什么时候才会优于另一种使得复杂操作代价减少. 类似的还有nfls集训 CF354D

杜赢的blog上的P8580 [CoE R5] 罚球

有 $n$ 个人在玩罚球游戏, 游戏规则如下:

每个人编号为 $1, 2, \dots, n$ , 最开始由 $1$ 号罚球, 接下来让下一个没有出局的人罚球. 特殊地, $n$ 号的下一个是 $1$ 号.

如果罚球者没有碰到篮板, 那么直接出局.

如果罚球者碰到篮板但没有进球, 那么如果上一个人进球了, 这个人就会出局, 否则不会出局.

游戏结束的条件是最后只剩下一个人.

注意最开始的那个人碰到篮板但没有进球不出局.

这 $n$ 个人中, 第 $i$ 个人碰不到篮板的概率为 $\dfrac{a_i}{1000}$ , 碰到篮板但没有进球的概率为 $\dfrac{b_i}{1000}$ , 求游戏结束时所有人总共罚球数量的期望值.

$n\le 18$

$n$ 很小, 直接状压, 设 $f_{S, i, 0/1}$ 表示还活着的是 $S$ , 然后现在是 $i$ 投球, 上一个人是否投中情况下期望值. 设 $next$ 表示 $i$ 之后下一个投球的人, 按照期望反向递推的套路写, 显然有:

$$
\begin{gathered}
f_{S, i, 0}=a_if_{S/i, nxt, 0}+b_if_{S, nxt, 0}+(1-a_i-b_i)f_{S, nxt, 1}+1\
f_{S, i, 1}=a_if_{S/i, nxt, 0}+b_if_{S/i, nxt, 0}+(1-a_i-b_i)f_{S, nxt, 1}+1\
f_{ {i}, i, 0/1}=0
\end{gathered}
$$

显然转移成环, 考虑分析:

首先, 环只有在同一个 $S$ 内部出现, $S$ 间不会有, 那么上来先按 $\vert S\vert$ 排序按顺序转移.

其次, 对于同一个 $S$ 内的, 发现 $f_{S, i, 1}$ 只在内部有环, 确定了 $f_{S, i, 1}$ 后 $f_{S, i, 0}$ 也只在内部有环, 考虑高消, 发现列出来每个方程都只有两个变量还是长成循环的样子, 用主元高消消元, 两个复杂度都是 $\vert S \vert$ 的.

主元高消指的是用一个变量表示其他变量(这也配起个名), 这里发现只要确定一个就能表示所有变量所以线性.

P2282 [HNOI2003]历史年份

给定由不超过2000个数字组成的字符串, 存在前缀 $0$, 按照一定规则将这些数字还原成正确的年份序列, 满足从小到大, 末尾最小在此基础上字典序最大.
$\vert s\vert \leq 2000$, 有多组询问.

容易想到满足末尾最小可以 $f_i$ 表示前 $i$ 个, 最后一个数是 $[f_i, i]$, 使最后一个数最小. 然后再一遍反着dp回来满足字典序.

此时dp式子大概是 $f_i=\max j \ s. t. \ c(f_j, j)<c(j+1, i)$, 因为字符串比较是 $O(len)$ 就成了 $n^3$

字符串比较容易优化: 只要先比较长度, 长度相同比较所在后缀字典序大小, 用SAM或SA都是 $O(1)$

优化dp: 填表形式需要每次给前面所有位置代表的 $c(j+1, i)$ 向后加一位, 不可做, 考虑刷表的时候一个 $i$ 一定贡献一个区间, 因为对 $c(i, j)$ 约束是一个下界, 所以区间赋值就能做.

因为还有一些 $0$, 使得你不能直接算长度, 而要预处理每个位置向左向右的 $0$ 长度并处理细节.

P2305 [NOI2014] 购票

今年夏天, NOI 在 SZ 市迎来了她三十周岁的生日. 来自全国 $n$ 个城市的 OIer 们都会从各地出发, 到 SZ 市参加这次盛会.

全国的城市构成了一棵以 SZ 市为根的有根树, 每个城市与它的父亲用道路连接. 为了方便起见, 我们将全国的 $n$ 个城市用 $1\sim n$ 的整数编号. 其中 SZ 市的编号为 $1$. 对于除 SZ 市之外的任意一个城市 $v$, 我们给出了它在这棵树上的父亲城市 $f_v$ 以及到父亲城市道路的长度 $s_v$.

从城市 $v$ 前往 SZ 市的方法为: 选择城市 $v$ 的一个祖先 $a$, 支付购票的费用, 乘坐交通工具到达 $a$. 再选择城市 $a$ 的一个祖先 $b$, 支付费用并到达 $b$. 以此类推, 直至到达 SZ 市.

对于任意一个城市 $v$, 我们会给出一个交通工具的距离限制 $l_v$. 对于城市 $v$ 的祖先 A, 只有当它们之间所有道路的总长度不超过 $l_v$ 时, 从城市 $v$ 才可以通过一次购票到达城市 A, 否则不能通过一次购票到达.

对于每个城市 $v$, 我们还会给出两个非负整数 $p_v, q_v$ 作为票价参数. 若城市 $v$ 到城市 A 所有道路的总长度为 $d$, 那么从城市 $v$ 到城市 A 购买的票价为 $dp_v+q_v$.

每个城市的 OIer 都希望自己到达 SZ 市时, 用于购票的总资金最少. 你的任务就是, 告诉每个城市的 OIer 他们所花的最少资金是多少.

$n\le 2\times 10^5$, 3s

容易想到dp, $f_u$ 表示 $u$ 的答案, 于是 $f_u=f_v+(dep_u-dep_v)p_u+q_u$, 其中 $v$ 是 $u$ 的祖先且 $dep_u-dep_v\le l_u$

然后这是个斜率优化, 考虑序列上的问题就直接斜率优化.

粗暴的做法是线段树套李超树, 出栈序+线段树套李超树.

Gym - 104128K NaN in a Heap

首先任意满足堆性质的都可以得到, 因为你从上往下插入肯定就不会发生调整了. 于是假如没有 nan且 $n=2^k-1$, 直接 $f_{i}$ 表示大小为 $i$ 的子树的答案即可, 转移就是 $f_i=\dfrac{1}{siz_i}f_{i/2}^2$.

那么如果有 nan, 转移的时候一方面要记录当前子树里有没有出现 nan, 一方面要把 $siz_i$ 改成 $siz_i-siz_{nan}$, 于是直接再加一维 $j$ 表示当前子树内 $nan$ 的大小, 没有则为 $0$, 就可以转移了.

然后想如果 $n\ne 2^k-1$ 怎么办, 发现大多数子树仍然是整的, 只有 $n$ 号点到 $1$ 号点这条链上大小不整, 那么再记录一维 $0/1$ 表示是不是整的子树状态下大小为 $i$ 的子树, 最后 $i, j$ 两维直接记的话都要开 map

CF1810G The Maximum Prefix

看起来是2021年夏令营的股票的加强版, 第一部分相同: 对于前缀和最大值, 如果从前往后dp比较困难, 需要记录当前前缀和和最大前缀和, 但从后往前dp则比较容易, 只需要记录最大值, 感觉因为加一个数对应的操作从局部的变成了整体的. 总之前缀和这种两边不对称的东西要都尝试一下.

于是 $f_{i, j}$ 表示还要走 $i$ 步, 当前前缀和最大值为 $j$ 的方案数, 那么 $f_{i+1, j}\cdot p_{i, c_i}\to f_{i, \max(0, j+c_i)}$ 就好了. 其中 $p_{a, 0/1}$ 表示在第 $a$ 步走 $0/1$ 的概率.

但问题是这样做不能一次得到所有前缀的答案, 需要dp $n$ 次, 注意到每次dp除了初始状态之外都是一样的, 那么对于这种很线性的dp可以先反向推出每个位置对答案的贡献, 然后直接统计贡献.

[trick] 只有加法乘法的dp可以递推出每个位置的起始值最后加到结果中的系数, 以处理多次询问

CF917C Pollywog

首先任意时刻青蛙一定在长度不超过 $k$ 的区间内, 因为一开始是这样的, 而后来怎么跳也不会改变这件事. 然后, $k$ 怎么才 $8$, 那就可以直接压出这 $2^8$ 种状态, 然后矩阵搞出转移. 特殊处理那 $q$ 个位置即可.

AGC018C Coins

考虑先让所有人选 $x$, 然后就是选 $y$ 个 $b-a$ 和 $z$ 个 $c-a$, 那么直接建图 $s \stackrel{(y/z, 0)}{\rightarrow} y/z, y/z\stackrel{(1, b_i-a_i/c_i-a_i)}{\rightarrow} i, i\to t$, 那么对着这个模拟费用流, 这题直接模拟比增量简单.

AT_arc085_d NRE

个全为 $0$ 的数组 $a$, 给一个数组 $b$ 和 $q$ 个操作, 每个操作将数组 $a$ 指定区间改成 $1$, 问合理选择部分操作后使得两个数组的 $\sum [a_i\ne b_i]$ 最小.

$n, q\le 2\times 10^5$

和前两天一个USACO2018Life Guards P一模一样啊()

右端点排序, 设 $f_i$ 表示前 $i$ 个区间最后一个区间必选开始dp, dp时分有交和无交用线段树维护转移即可.

AT_abc304_g Max of Medians

给定一个长度为 $2N(1\le N\le 10^5)$ 的序列 ${A_i}(0\le A_i< 2^{30})$, 你需要将其中元素两两配对并求异或和, 得到 $N$ 个数的集合 $B$. 最大化 $B$ 的中位数, 其中集合的中位数定义为将集合排序后得到序列的第 $\lfloor\dfrac N2\rfloor + 1$ 项.

用 $u_0, u_1$ 表示 $u$ 在01trie上的儿子.

看见中位数, 二分答案, 变成只有大于 $x$ 的能匹配求最大匹配.

然后建01trie贪心匹配, 从高到低遍历 $x$ 的位同时在trie上从根往下走, 前若干位是 $0$, 此时肯定优先跨子树匹配, 把多的那边剩下的数递归下去, 然后出现一个 $1$ 就要跨子树匹配了, 设 $f(u, v)$ 表示 $u$, $v$ 之间匹配最大数量, 那么如果此时 $u, v$ 所在层对应 $x$ 为 $1$ 就只能跨子树匹配 $u_0, v_1$ 和 $u_1, v_0$, 否则若剩下了还可以匹配 $u_0, v_0$ 或 $u_1, v_1$, 就做完了.