杜赢OJ选做
21 BCT NOIP Day 1-2 暨<高龙强总结>登顶纪念赛
[21 BCT NOIP Day 1-2] 宝石 (gem)
智障题
[21 BCT NOIP Day 1-2] 小恐龙 (dino)
位置 $x$ 可以跳到 $x+1$ 或 $x+k$ , 若目标位置有障碍则不能跳, $q$ 次询问, 每次将一个格子变成障碍或者求恰好到第 $x$ 个格子的最小大跳(跳长 $k$ 的)次数.
$n, q\le 2\times 10^5, k\in [\dfrac{n}{100}, n-1]$
我天看错题了!
看这个 $k\ge \dfrac{n}{100}$ 的特殊含义.
考虑一个朴素dp, $f_i$ 表示跳到 $i$ 的次数.
那么 $f_i$ 总和是 $100n$ 的. 考虑把这个做为势能.
那倒着做, 一开始每个势能都当成 $101$ , 每次会让一个位置能用, 就暴力更新它能更新到的所有位置, 如果一个位置更新了就往下接着更新否则就停, 就做完了.
[21 BCT NOIP Day 1-2] 序列 (sequence)
给定序列 $a_n$ , 对每个 $k\in [2, n]$ , 求最短的区间 $[l, r]$ 满足在这个区间的数在 $a$ 中至少连续出现了 $k$ 次.
你的答案正确当且仅当与标准答案相对误差在 $6%$ 以内.
$n\le 10^5, a_i\le 10^6$
这个 $6%$ 那必然是做法的关键.
考虑此时, 若真实答案是 $c$ , 那么 $[0. 94c, 1. 06c]$ 的答案都可以由 $c$ 表示. 那么你发现实际上 $10^6$ 种不同的答案可以由不到 $200$ 个 $c$ 表示.
那你就考虑对每个答案求连续出现长度, 如果值域上, 就是01序列, 支持单点改, 查全局最长连续段长度, 好像很难线性. 但从序列上是简单题, 双指针就完了.
[21 BCT NOIP Day 1-2] 基础计数练习题 (count)
居然是CF1237F Balanced Domino Placements.
21 BCT NOIP Day 1-1 暨 LKawaii AK 纪念赛
[21 BCT NOIP Day 1-1] 星形 (star)
给一个 $n$ 个点的树, 要删掉若干个点使得这棵树变成星形, 求方案. 星形定义是恰好一个点度数大于 $2$
$n\le 5\times 10^5$
直接枚举每个节点为根去计数即可.
[21 BCT NOIP Day 1-1] 树状数组 (fenwick)
给定序列 $a_n$ , $q$ 次操作, 每次对区间 $\forall i\in[l, r]$ , 给 $[i-\mathrm{lowbit}(i), i]$ 加 $v$ , 或求区间和.
$n\le 10^6$
把序列补齐成 $2$ 的幂, 则线段树节点和树状数组节点对应.
维护区间加标记和区间树状数组节点加标记, 树状数组节点加标记表示编号在这一区间的树状数组节点全被加了一个数值, 修改时如果被完整包含就给树状数组加标记加, 并且视情况打区间加. 因为可以预处理每个区间的树状数组加的实际对和大贡献所以可以合并标记. 复杂度 $m\log n$ .
[21 BCT NOIP Day 1-1] 多叉树 (ktree)
给一个深度为 $n$ 的满 $k$ 叉树, 叶子节点权值初始为0, 非叶子节点权值为儿子之和. 一次操作可以给一个叶子加1, 求有多少操作序列满足, 对于任意一个节点 $u$ , $u$ 的儿子中权值的极差不超过1, 且满足 $m$ 条限制, $i$ 条是 $t_i$ 次操作的叶子必须是 $x_i$ .
膜998244353, $k\le 10^6$
考虑 $m=0$ 怎么做, 显然我们每次是对所有节点”轮着”加, 那么设 $f_n$ 表示深度为 $n$ 的答案, 发现 $f_n=f_{n-1}\times (k! )^{k^{n-1}}$
解释就是经过 $k^{n-1}$ 次操作, 所有 $n-1$ 层节点的权值就会加1, ${(k! )}^{k^{n-1}}$ 就是考虑了这 $k^{n-1}$ 个第 $n-1$ 层的节点的孩子们加的顺序, 但还没考虑这 $k^{n-1}$ 个节点之间的顺序, 这个问题可以把这些节点视作叶子递归到 $f_{n-1}$ .
那么现在有了限制, 假设某个点的儿子种有 $x$ 个被固定, 显然方案数是 $(k-x)!$ , 那么分治的时候将限制分治到对应的儿子下面即可, 分治后有可能要对着同一个叶子加两次那就死了.
[21 BCT NOIP Day 1-1] 括号序列 (bracket)
一个长 $2n$ 的括号序列是由 $n$ 种括号构成的序列, 保证每个括号只出现一正一反, 给出长 $2n$ 的序列 $a$ , 求方案把 $a$ 划分成两个子序列且子序列的括号配对合法.
$\sum n\le 1. 5\times 10^6$
感觉D < C啊.
考虑两个括号相交如 $\texttt{[(])}$ , 则必须分属不同的子序列.
那么你得到一个暴力建边+黑白染色的方法, 考虑如何在不建边的情况下做这个东西.
首先显然的, 把括号视作区间 $[l, r]$ , 那么相交的括号 $[x, y]$ 满足的限制是平面上两个 3-side 矩形. 也就是一个点连向一个矩形.
那么自然想到KDT, 但这里 $10^6$ 肯定过不了, 另一个想法是主席树优化建图(因为两个矩形都是3-side), 但常数太大实际也过不了.
考虑,数点实际上是丢了性质, 考虑从左往右扫, 把每个区间挂在右端点上, 当处理到 $[l, r]$ 时, 所有还挂在这个区间上的都作为它的儿子, 钦定 $[l, r]$ 是黑色, 那么可能会对所有儿子反色(子树取反), 这样求出来再check即可.
当我们不能建出所有关系的时候可以考虑把必要的关系建出来再判能不能行.
21 BCT NOIP Day 2 暨 Dowt 总统膜拜功能上线纪念赛
[21 BCT NOIP Day 2] 成绩 (score)
两个随机排列 $a_n, b_n$ , 定义一个元素的排名它在两个排列中的位置之和的排名, 为现在已知某元素在第一个排列中位置为 $x$ , 第二个排列位置为 $y$ , 求它排名的期望.
膜998244353.
$n\le 998244352$
用概率去考虑, 那么它的期望是每个元素在它前面的概率之和. (可以从期望的线性想).
那么一个元素在它前面的概率, 对于一个元素确定的在 $a$ 中排名 $u$ , 其 $b$ 中排名 $v$ 的可能取值是一个区间, 那就直接等差数列求和即可.
[21 BCT NOIP Day 2] 插旗 (flag)
给定一棵 $n$ 点树, 每次你可以跳到一个当前没走过且距离不超过 $k$ 的位置, 求最小的 $k$ 可以走过树上所有点.
$n\le 10^4$
考虑, 要走到一个子树一定要先走到其根, 并且我们要走一圈上来, 而我们希望最后一次往上跳的一布越靠上越好, 于是设 $f_u$ 表示 $u$ 出发从子树走一圈最后上来的那个节点的深度最小值, 每次会从最小的 $f_v$ 转移上来, 就行了.
[21 BCT NOIP Day 2] 括号序列加强版 (bracketplus)
小 T 得到了一个序列 $a$ . 如果一个序列能被看作一个括号序列, 那么小 T 称这样的序列为符合规范的超级括号序列.
“符合规范的超级括号序列”的定义如下:
- 空序列, $S S$ 均是符合规范的超级括号序列, 其中 $S$ 表示一个在 $[1, n]$ 之间的正整数(以下规
则中的 $S$ 均为此含义);- 如果 $A$ 为非空的符合规范的超级括号序列, 那么 $S A S$ 为符合规范的超级括号序列;
- 如果 $A$ 和 $B$ 均为符合规范的超级括号序列, 那么 $A B$ 为符合规范的超级括号序列;
- 所有符合规范的超级括号序列均可通过上述 $3$ 条规则得到.
小 T 想知道有多少 $a$ 的非空子区间使得它是符合规范的超级括号序列.
$n\le 3\times 10^5$
对着一个降智题想了一年并没想出来. 昨天qyc题明明是一样的技术
考虑判定一个整的可以直接用一个栈, 从左往右扫, 和栈顶一样就弹栈, 不一样就压栈.
然后发现一个区间合法当且仅当它这个栈在左端点和右端点长的一样, 直接hash就做完了.
[21 BCT NOIP Day 2] 研究表明 (string)
给定一个01串 $a$ , 若 $a$ 生成 $b$ 当且仅当存在排列 $p_n$ 满足 $\forall i\in [1, n], -1\le p_i-i\le k, b_{p_i}=a_i$ , 其中 $k$ 为给定的正整数, 求给定的 $a$ 的所有子区间能生成的01串个数之和. 并且因为 $a$ 太长了, 其是由输入串 $c_n$ 重复 $t$ 次得到的.
$n\le 2\times 10^6, t\le 10^9, k\le n-1$
考虑对循环移位进行分解, 发现一定可以分解成0 0 0 0 1或1 1 1 1 0这样的段, 那么设 $f_i$ 表示以 $i$ 结尾的方案数, 发现它是区间 $f_j$ 和再加1得到. 而最后的答案就是 $f$ 的和, 发现这里暴力转移(而不是前缀和)的复杂度是对的, 因为它必须是一个01切换的时候付出前面连续段长度的代价. 现在可以做到 $nt$ 了.
考虑在这个基础上再进行一轮dp这个过程, 实际上只是给 $f_1$ 了一个初值, 而其他都没有变. 发现我们因为每次是一个求和, 所以实际上整个dp的值是一个一次函数, 把一次函数的值像这样复合到自己同样是一次函数, 所以我们是线性变换, 所以dp一轮直接写成矩阵快速幂即可.
21 BCT NOIP Day 3-1 暨 gxd 停课纪念赛 & 简单题信心赛
[21 BCT Day 3-1] A
智障题
[21 BCT Day 3-1] B
给定序列 $a_n$ , 求最长的子序列 $c_k$ 满足 $c_i=c_{i-1}+c_{i-2}$
直接设 $f_{i, j}$ 表示以 $i$ 结尾, 上一个是 $j$ 的序列长度.
那么它能由 $f_{k, l}$ 转移过来, 当且仅当 $a_k=a_j$ 且 $a_l=a_i-a_j$ .
开个map.
[21 BCT Day 3-1] C
给出一个 $n$ 个点的完全二叉树, 点有点权, 定义一个大小为 $k$ 的连通块 $s$ 的 $f_a(s)$ 为其第 $\lfloor\dfrac{k-a+1}{2}\rfloor$ 大的元素, 则对每个 $a\in [0, n-1]$ 输出 $\max_s f_a(s)$
$n\le 2\times 10^5, w_i\le n$
考虑序列上怎么做, 考虑对于一个确定的 $a$ 判定一个答案, 把大于它的设为 $1$ , 小于它的设为 $-1$ 若最大子段和不小于 $a$ 就是对的.
那么对于所有 $a$ , 只要从小到大枚举一个答案, 每次区间赋值即可.
那么现在搬到树上, 就是要维护最大子连通块和即可. 这里暴力dp就行.
[21 BCT Day 3-1] D
给定序列 $a_n$ , $m$ 次查询区间 $[l, r]$ 中最长的值域不等于 $[l, r]$ 的值域的子区间.
$n, m\le 2\times 10^6$
考虑这个相当于求区间内, 相同值的相邻最大距离, 且把区间端点视为和所有数相同. 发现完整包含区间内的和与区间端点形成的都可以直接数点, 就做完了.
另一个想法是考虑直接扫描线, 扫右端点维护左端点出发的答案, 那么每次就是给一个区间取 $\max$ , 因为单调所以是区间赋值.
22 正睿 AB班 DAY 1 暨 lixp 粉丝线下见面会
[22AB Day1] 谁是演员
给定正整数 $n$ 和一个长度为 $n$ 的序列 $a_1, a_2\ldots, a_n$ . 你需要将序列划分成 $k$ 个连续段, 每段的权值是内部序列的极差, 你需要最大化所有段的权值和. 你需要对 $k=1, 2, \ldots, n$ 求出答案.
$n\le 10^5$
首先简单分析能得出极差这个函数是凸性的, 那么再用经典DAG定长最短路结论能得到整个答案也是凸性的.
考虑把答案看成一个函数 $f_i(x)$ 表示 $i$ 管辖的段中, 分 $x$ 段的方案. 那就直接分治, 每一层通过凸函数合并(闵和)得到答案. 复杂度就是 $n\log n$ . 然后比较麻烦的是要考虑中间那一段最大值在左/右边.
这个题的启发仍然是把dp看作函数, 提醒我们凸性dp可以看成函数跑闵和.
[22AB Day1] T-90A
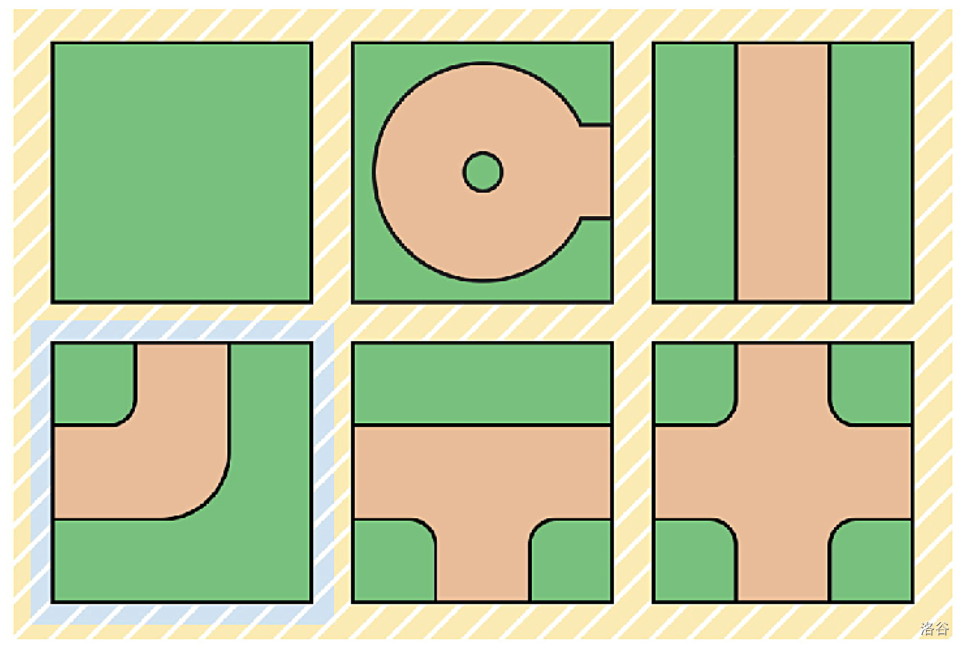
你是一个水管工. 有一个 $n\times m$ 的长方形网格, 每一个格子的水管可以为以下这几种类型之一:
注意上述水管可以旋转. 我们称第四种水管(蓝色高亮标识)为高级的. 如果一个局面中每个位置都放置了如上六种水管之一, 并且所有水管都连起来了(每条水管接口都与相邻的水管相连), 那么就称这个局面是合法的. 注意不能朝向边界外.
目前有一些格子中放置了高级水管, 你能在若干个其他格子中放置一些高级水管. 在此之后, 你的同伴——另一个水管工会尝试在剩余未被放置水管的格子中放置水管, 使得最终变成一个合法的局面. 注意你和你的同伴不能旋转那些提前放置的水管. 此外, 对某些格子, 你不能够在其中放入高级水管, 并且对另外某些格子, 你必须要在其中放入一种高级水管.
你需要求出在你放完高级水管之后最多有多少个格子中为高级水管, 并使得你的同伴能完成工作. 如果无解, 输出 $-1$ .
$n, m\le 100$
把格子建成网格图, 一个高级水管等价于一个格子的对边两两连通性不同. 且发现其他情况是任意的.
困难的, 不会.
[22AB Day1] 探查民情
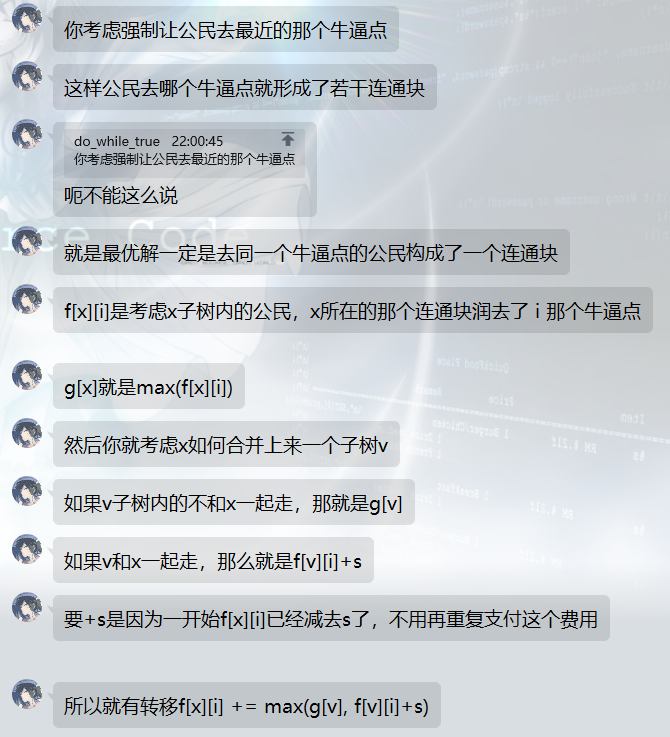
给一棵 $n$ 点树, 点有点权 $a_i$ , 边长度, 你要选择点集 $A$ , 获得 $(\sum_{u\in B} a_u t)-s\vert A\vert$ , 其中 $B$ 是所有到 $A$ 中点距离不大于 $d$ 的点. $s, t, d$ 为常数.
$n\le 1000$
考虑树形dp如何计算子树对外面的影响, 发现取决于子树内最浅的在 $A$ 中的点(可能让一些子树外的 $B$ 加入贡献)或子树内最深的不在 $B$ 的点(可能让子树外的时候因子树内的 $B$ 贡献), 于是直接记录这两个dp, 可以达到 $n^3$
然后你发现实际上要么子树内延伸到外面, 要么外面到子树内, 两个事不会同时发生, 所以你只用记录一个, 就 $n^2$ 了.
杜赢提供了更厉害的做法
22 正睿 AB班 DAY 10 暨 lkw 人赢经验分享
A. [22 AB Day10] 签到
问所有长度为 $n$ 的合法表达式, 其中其中每个字符一定是 $\texttt{123456789+*}$ 中的一种, 运算结果的和.
一个表达式合法当且仅当:
首尾字符不能是 $\texttt{+}$ 和 $\texttt{*}$ .
不能连续两个字符是运算符号.
输出答案对 $998244353$ 取模的结果.
$n\le 10^18$
考虑表达式像是被加号分割单若干个连乘的部分, 那么记录最后一个加号前的和, 最后一个加号往后乘积, 以及最后一个乘号之前到最后一个加号这一部分的乘积, 设为向量 $v=[a, b, c]$ , 则后面增加一个数字 $d$ 会变成 $[a, 10b+cd, c]$ , 加一个乘号变成 $[a, b, 0]$ , 加一个加号变成 $[a+b, 0, 1]$ .
于是假设三个转移分别写成变换矩阵 $A, B, C$ , 要求 $v$ 乘上 $A, B, C$ 组成的一个序列的和, 你发现这玩意实际是 $v(A+B+C)^n$ , 那就直接矩阵快速幂. 但是它要求不能有两个符号接起来的, 所以实际上是 $v_i=v_{i-1}A+v_{i-2}(B+C)A$ 的 $v_n$ , 矩阵大小是7.
[think] 对线性变换做线性变换还是线性变换, 如这里后面加一个是线性变换, 那么整体求和仍然是线性变换.
[think] 如果范围给你矩阵快速幂的感觉, 但转移不线性, 那么枚举状态设计可能会让它线性.
B. [22 AB Day10] 送分
给定 $n$ 个点 $(x_i, y_i)$ , $x_i$ 互不相同, 询问矩形内任选两点连线斜率最小值是多少.
$n\le 7000, q\le 7\times 10^5$
结论数据结构题.
[trick] 斜率最小的两点一定是 $y$ 方向上最接近的两个点.
然后就是简单题了, 在 $x$ 方向上扫描进行莫队, 维护 $y$ 方向上两相邻点之间的斜率即可. 复杂度 $n\log n\sqrt q$
22 正睿 AB班 DAY 2 暨 hws 粉丝线下交友会
A. [22 AB 联考 Day2] 序列
给定 $a_n$, $q$ 次问区间 $[l, r]$ 中有多少子区间使得区间内部不同数的个数为奇数.
$n, q\le 5\times 10^5$
考虑扫描线, 维护每个左端点到当前右端点的区间内不同数个数. 于是每次加一个数是给区间奇偶性取反.
然后问题变成了要累加这么个东西, 那这个就是把询问挂在右端点, 扫描到右端点的时候问区间历史和. 扫到左端点的时候也要问(差分一下).