LYHDP选做
LYHDP
slide. pptx
day6那个做不动啊, 还是看看简单点的.
CF1409F Subsetsequences of Length Two
给定 $s_n, t(\vert t\vert=2)$ , 可以修改 $s$ 的最多 $k$ 个字符使得 $t$ 作为子序列在 $s$ 中出现次数最大.
$n\le 200$
$f_{i, j, k, l}$ 表示前 $i$ 个, 修改 $j$ 个, $t_1$ , $t_2$ 的个数分别为 $k, l$ 的 $t$ 出现次数.
哦, $t_1, t_2$ 只需要记录一个.
CF1404B Tree Tag
给定一棵树 $T=Tree(n)$ , $AB$ 初始时在 $a, b$ 两点, 每次可以移动到距离不超过 $d_a, d_b$ 的点, 交替移动 $A$ 先手, 若 $A$ 能抓住 $B$ , $A$ 获胜. 问谁赢.
$n\le 10^5$ .
考虑因为无限步数, 可以忽略前面过程, 直接想什么时候必然抓住:
- $A$ 站在直径中点上, $B$ 死了
- $d_b\le 2d_a$ , 此时它不能跨过 $A$ , 那 $A$ 只要一步一步压缩即可.
- 一开始 $B$ 离 $A$ 太近
CF1349C Orac and Game of Life
给定 $n\times m$ 01矩阵, 每次若一个位置与它四连通的位置01相同就取反, $q$ 次询问 $i, j$ 在 $p$ 秒后是几.
$n, m\le 1000, t\le 10^5, p\le 10^18$
一个连通块总是同步的, 可以缩起来.
如果一个格子某一时刻变了, 那么它接着会一直变.
于是直接求每个格子最早的变化时间(容易发现非常早), bfs一遍转移.
CF1338B Edge Weight Assignment
给定无根树 $Tree(n)$ , 为每条边赋值 $w>0$ , 使得任意两个叶子路径异或和为0, 求最少最多的颜色数.
$n\le 10^5$
要求任意两个叶子中所有数出现偶数次, 那最少的情况显然可以中间的全相等, 在叶子上调整(再找两个数异或等于刚才的数一调就行了).
最多的情况, 考虑一个点的所有叶子儿子到它的边要相同, 除了这个之外都可以不同(初始化一个相同的解, 然后在非常高的位置调整出一个1)
CF1334D Minimum Euler Cycle
给定 $n$ 点的有向完全图(任意两点之间有两条边), 求字典序最小的欧拉回路的第 $l$ 到第 $r$ 个点.
$n\le 10^5$
出发位置是最小值, 以后每次走出边最小的就是策略了.
考虑这么做形成若干个环, 对每个点统计这里出发的环的大小? 不对.
降智, 正确做法: 完全图, 所以实际上你可以任意走, 要保证每条边正反各一次, 直接构造:
$1\to 2\to 1\to 3\to \ldots 1\to n\to 2\to 3\to 2\ldots$
CF1329A Dreamoon Likes Coloring
你有序列 $a_n$(初始为 $0$) , 进行 $m$ 次区间 $l_i, r_i$ 赋值 $i$, 要求最后每个颜色 $i>1$ 出现至少一次, 且 $a_i\ne 0$. $r_i-l_i+1$ 给定, $l_i$ 不给定.
$n, m\le 10^5$
考虑直接把 $l$ 对应 $r$ 排序然后随便模拟.
CF1322B Present
给定 $a_n$ , 求 $a$ 中任意两数对的和的异或和.
$n\le 4\times 10^5, a_i\le 10^7$
每一位分别考虑, 要求一个数与其他所有数在第 $i$ 位上为 $1$ 的个数. 两种情况: 要么是直接加的, 要么是进位出来的.
进位就是每个数只取前 $k-1$ 位, 加起来大于 $2^k$ , 于是可以直接做了.
CF1320C Battle for Azathoth
矩形加-最大矩形和, 扫掉一维即可.
CF1312E Array Shrinking
直接区间dp, 注意若一个区间可以合并成单点, 这个数是唯一的.
CF1288D Minimax Problem
二分答案+变成一堆二进制数或起来全1+FMT. 想不到吧, 是可以直接枚举两个二进制数的(值域很小)
CF1276B Two Fairs
$a, b$ 是割点, 于是图分成三部分, 答案是两边两部分的积.
哦, $a, b$ 不一定是割点, 而是删掉它们之后, $u, v$ 是分别只和 $a, b$ 相连的两部分.
CF1213G Path Queries
离线排序从小到大, 问连通块平方和之类的.
CF1030E Vasya and Good Sequences
可以对每个数都把一整到最前面, 一定不劣? 不对, 比如6, 7, 14这个样的, 你会让它们下面的抵消, 最后用6消掉上面的.
于是实际条件是, 1的个数为偶数, 并且最大的数的1的个数不超过总共个数的一半, 发现不满足第二个限制的区间最长是 $w$ 的, 于是暴力即可.
CF959E Mahmoud and Ehab and the xor-MST
异或和为1的会连接任意 $2i, 2i+1$ .
异或和为2的会连接差2的点.
发现加入异或和为 $2^i$ 的会合并前 $2^i$ 位, 其他的不会合并.
于是答案就是
$$
\sum_i \lfloor \dfrac{n}{2^i*2} \rfloor 2^i
$$
CF900D Unusual Sequences
都除以 $x$ , 问题变成互质序列加起来是 $\dfrac{y}{x}$ 的方案数.
没有互质可以直接隔板法是 $2^{y-1}$ . 于是你就容斥, $g(x)$ 表示 $\gcd$ 为 $x$ 的因数的方案数, $f(x)$ 表示恰好为 $x$ 的方案数, 莫反即可.
CF859D Third Month Insanity
直接dp, 一遍算在点 $u$ , $x$ 获胜的概率, 一遍dp点 $u$ 子树内走到 $u$ 的是 $i$ 的情况下得分期望和.
CF853C Boredom
简单容斥+二维数点
CF1408E Avoid Rainbow Cycles
考虑把图简化, 一个集合连一个团可以变为给每个集合建一个点, 集合内的点向它连边.
此时原边权是现在两条边中间那个点的点权.
发现因为集合每个点多颜色是唯一的, 这样做又不会形成同集合的环, 所以只要有环就是rainbow.
然后开始想什么网络流建图可以约束没有环这一条件, 哦, 是最大生成树啊/hanx.
CF1217E Sum Queries?
给你 $n$ 个数 $a_i$ .
对于一个子序列 $p$ , 定义 $s_p$ 为子序列中所有数的和.
定义一个子序列 $p$ 是好的, 当且仅当 $s_p$ 用十进制表示时, 对于 $\forall i$ , 都能在子序列 $p$ 中找到一个数 $x$ , 使得 $s_p$ 从低到高的第 $i$ 位与 $x$ 从低到高的第 $i$ 位相等.
你需要对序列 $a$ 做 $2$ 种操作:
- 把 $a_i$ 修改成 $x$ .
- 在 $a_l, a_{l+1}\cdots, a_r$ 构成的序列中, 找一个 $s_p$ 最小的子序列 $p$ , 使得 $p$ 是坏的. 你需要输出 $s_p$ . 如果不存在, 输出 $-1$ .
$1\le n, m\le 10^5, 1\le x, a_i<10^9$
考虑如果一个集合是坏只要有一位不全为0. 于是每一位开线段树维护最小值和次小值.
CF1215E Marbles
有 $n (n \le 4 * 10^5)$ 个珠子 , 第 $i$ 个珠子颜色是 $c_i (c_i \le 20)$ , 每次操作把相邻的两个珠子交换. 现在要把相同颜色的珠子排列在相连的一段, 问至少要多少次操作 .
给珠子钦定一个顺序之后就是排序了, 排序是好做的.
那么设 $cost(a, b)$ 表示 $a$ 排在 $b$ 之后的代价, 直接状压dp即可.
CF1188C Array Beauty
定义一个序列 $b_1, \ldots, b_n$ 的美丽值为 $\min_{1 \leq i < j \leq n}{\vert b_i-b_j\vert }$ . 给定一个长度为 $n$ 的序列 $a$ , 求 $a$ 的所有长度为 $k$ 的子序列的美丽值之和对 $998244353$ 取模的结果.
$2 \leq k \leq n \leq 1000$ , $0 \leq a_i \leq 10^5$ .
先枚举一个美丽值, 计算有多少个子集.
把 $a$ 排序.
$f_{i, j}$ 表示 $a$ 的前 $i$ 个里选 $j$ 个, 美丽值大于当前值的方案数, 复杂度 $n^2$ . 或者确切的, $nk$
似乎过不了, 但是你再想想, 值域其实不是 $\max a_i$ , 而是 $\dfrac{\max a_i}{k - 1}$ ! 你就过了.
[think] 分析复杂度确切一点!
CF1111E Tree
给定 $Tree(n)$ , $q$ 次询问给定 $k, m, r, a_k$ , 求将 $a_k$ 中点分为不超过 $m$ 组使得以 $r$ 为根的时候没有同组两点有祖先关系的方案数. 膜 $10^9+7$
$n, q\le 10^5, m\le \min(k, 300)$
直接虚树dp, $f_{i, j}$ 表示以 $i$ 的子树内分 $j$ 组的方案. 问题是合并两个子树信息的时候, 可能有跨过子树的组, 我们也不知道怎么办了(
枚举扫描线方向, 子树dp相当于从儿子到祖先, 考虑先祖先再儿子, 于是想到dfs序排序, 设 $f_{i, j}$ 表示前 $i$ 个点, 分 $j$ 组, 那么点 $i$ 的不能和它的祖先一组, 可以挤进去或者新开一组, 简单 $nm$ .
那么现在也不用虚树了, 只要求有多少个祖先是关键点, 简单单点加链求和.
但实际上手够硬也是可以的, 考虑一开始组带着标号算, 并且允许空组, 此时两个子树合并的时候就是直接 $f_{i, j}$ 相乘, 因为就相当于一共有这么多组, 每次把一个子树的东西填进去, 合并两个子树的时候就是直接对应相乘, 容斥出非空盒子个数除掉阶乘即可. 复杂度相同.
[think] 树上dp的扫描线方向, 带标号简化问题+容斥.
CF1097D Makoto and a Blackboard
给定 $n, k$ , 一共会进行 $k$ 次操作, 每次操作会把 $n$ 等概率的变成 $n$ 的某个约数
求操作 $k$ 次后 $n$ 的期望是多少, 答案对 $10^9+7$ 取模
$1 \le n \le 10^{15}, 1 \le k \le 10^4$
考虑把 $n$ 质因数分解, 发现答案关于每个因子 $p^a$ 是独立的, 此时就可以直接计算了.
[think] 计数要找独立! 独立!
CF1044D Deduction Queries
给定 $a_n$ 和 $q$ 次操作 $(1 \leq q \leq 2 \times 10^5)$ , 两种操作类型:
1, l, r, x: 表示已知 $a$ 的区间 $[l, r]$ 的异或和为 $x$ , 或者与已知矛盾忽略.2, l, r: 表示询问 $a[l, r]$ 的异或和或判断不可知.
强制在线. $(0 \leq l, r, x \leq 2^{30})$
它确实长了一张并查集的脸啊!
考虑带权并查集, 每个点维护到根的点的异或和, 就行了.
CF1043F Make It One
在数数题里.
CF891C Envy
给出一个 $n$ 个点 $m$ 条边的无向图, 每条边有边权, 共 $Q$ 次询问, 每次给出 $k_i$ 条边, 问这些边能否同时在一棵最小生成树上.
$n, m, q, w, \sum k_i\le 5\times 10^5$
考虑Kru的过程, 那么一条边权为 $w$ 的可以在最小生成树上当且仅当所有边权小于 $w$ 的都被插入之后 $w$ 两端点不连通. 于是如果询问边权没有相同的可以直接可持久化并查集. 如果有相同的元素按照任意顺序都是对的, 于是按照任意顺序一个一个合并进去即可.
哦, 实际上可以干掉可持久化, 建操作树+撤销即可.
CF875F Royal Questions
给定二分图, 左边 $n$ 个点, 右边 $m$ 个点, 右边第 $i$ 个点连向左边第 $a_i$ , $b_i$ 个点, 权值为 $w_i$ , 求权值最大的匹配.
$n, m\le 2\times 10^5, w_i\le 10^4$
将右边点看成边, 于是一个连通块合法当且仅当是基环树或树. 于是用最大生成树的做法去做.
[think] 枚举多种建图方式.
CF870E Points, Lines and Ready-made Titles
在一个平面上有 $n$ 个不同的点( $n$ 给出). 而对于每一个点而言, 你可以对它作一条垂直线, 也可以作一条水平线, 并且也可以不对它进行任何操作. (若有重合的线段则视为一条直线). 请问你能得到多少种不同的图片呢? 得出的答案对 $10^9+7$ 取模.
考虑点相互影响的关系, 发现只有在同一水平竖直线才相互影响, 于是每个点向四方向最近点连边, 拆成若干个独立连通块.
考虑单独计算一个连通块, 结论是, 对于一个连通块, 如果是树, 答案为 $2^{A+B}-1$ , 否则是 $2^{A+B}$ .
考虑如果一个连通块是树, 选择一个根, 钦定其方向, 然后让每个点和父亲的方向不相同, 发现可以铺满除了根所在的所有行/列, 于是只有全满的一种方案无法选择. 如果一个连通块有环, 此时选择环上一点做为根, 就能全满.
CF868F Yet Another Minimization Problem
显然四边形不等式. 直接分治决策单调性. 然后这个是莫队+分治的那个trick(分治的时候用莫队计算决策, 端点移动量级是 $n\log n$).
CF856B Similar Words
单词是由小写英文字母组成的非空串.
若一个单词去掉首字母后与另一个单词相同, 则这两个单词相似.
现给定 $n$ 个单词(可能重复), 请挑选尽量多的新单词组成集合 $T$ 并满足条件:
- $T$ 中的新单词为原 $n$ 个单词的前缀(包含自身)
- $T$ 中的新单词两两不相似.
求 $\max \vert T \vert$
$\sum s_i\le 10^6$
考虑先求出所有前缀和每个前缀相似的字符串, 可以用hash, 把看每个前缀向删掉第一个字符之后得到的点连边, 最后就是选最多的点使得没有两点有父子关系, 直接树形dp.
CF815C Karen and Supermarket
在回家的路上, 凯伦决定到超市停下来买一些杂货. 她需要买很多东西, 但因为她是学生, 所以她的预算仍然很有限.
事实上, 她只花了 $b$ 美元.
超市出售 $n$ 种商品. 第 $i$ 件商品可以以 $c_i$ 美元的价格购买. 当然, 每件商品只能买一次.
最近, 超市一直在努力促销. 凯伦作为一个忠实的客户, 收到了 $n$ 张优惠券.
如果 Karen 购买第 $i$ 件商品, 她可以使用第 $i$ 张优惠券, 将该商品的价格减少 $d_i$ 美元. 当然, 不买对应的商品, 优惠券不能使用.
然而, 对于优惠券有一个规则. 对于所有 $i\ge 2$ , 为了使用第 $i$ 张优惠券, 凯伦必须也使用第 $x_i$ 张优惠券 (这可能意味着使用更多优惠券来满足需求. )
凯伦想知道. 她能在不超过预算 $B$ 的情况下购买的最大商品数量是多少?
$n\le 5000$
考虑 $x_i$ 形成的结构显然是森林, 依赖是自顶向下的, 设 $f_{u, i, 0/1}$ 表示 $u$ 子树内是否使用优惠卷, 此时用了 $i$ 元的最大收益, 不行, 换成买 $i$ 件物品的最少价格, 转移就是背包.
CF804D Expected diameter of a tree
给一片森林, $q$ 个询问, 每个询问两个点, 问从这两个点所在的连通块内各自均匀随机两个点, 连接起来组成的新连通块, 它的最远两点的距离的期望值是多少.
$n, q\le 10^5$
先考虑一次询问.
一个点的贡献是 $b(\max_i dis_{u, i}+\dfrac{1}{2})$ , 其中 $b$ 为对面集合的大小, 那就对每个集合维护这个即可. 显然 $u$ 是两个直径之一.
不对, 新直径可能是原来两个连通块的直径.
那么算两个集合的和小于 $x$ 的个数和总和, 考虑分别排序, 那么双指针就能算. 或者在里面二分+前缀和.
现在多次询问, 不会了.
好厉害的自然根号, 考虑如果二分+前缀和, 我们的询问只与小的那个大小有关, 对于小于 $\sqrt n$ 的连通块算一次是 $\sqrt n$ , 对于大于 $\sqrt n$ 的只有 $\sqrt n$ 个大于它的, 所以只要对大于 $\sqrt n$ 的记忆化复杂度就是1log.
[think] 总和为 $n$ 的集合, $\sum_a \sum_b \min(a, b)\le O(n\sqrt n)$
CF600E Lomsat gelral
模板-线段树合并
CF1379F2 Chess Strikes Back
给出一个 $2n\times 2m$ 的黑白交错棋盘, 其中格子 $(1, 1)$ 为白色. 每次拿走或放回一个白格, 问能否在剩下的白格中放入 $n\times m$ 个国王使得它们不互相攻击.
$n, m, q\le 2\times 10^5$
考虑有解条件, 首先这个 $n\times m$ 和 $2n\times 2m$ 的关系不是没用的, 考虑分成 $2\times 2$ 的块, 于是任意一个块里恰有两个白格, 一个国王. 形成了一个类似2sat的限制, 图上显然只有偶环.
没前途, 2sat的模型并不适合性质, 考虑一个矩形, 发现要确定对角顶点的状态才唯一, 于是发现没有一方格满足, $A$ 左上角不能放, $B$ 右下角不能放, 且 $B$ 在 $A$ 的右下方, 仅在此时中间的矩形不满足. (否则, 一定在内部已经出现这样的格子对).
于是直接线段树维护两种最靠左上的 $A$ 和最靠右下的 $B$ 即可.
CF1310C Au Pont Rouge
给出一个长度为 $n$ 的字符串 $S$ 以及整数 $m, k$ .
对于一个把 $S$ 分割成非空的 $m$ 段的一个方案, 我们用这个方案中分割出的字典序最小的一个串代表这个分割方案.
eg. $S=abaabb, m=3$ , 存在分割方案 ${ab, aab, b}$ , 则我们用字典序最小的 $aab$ 来代表这个分割方案.
现在把所有分割方案对应的代表该方案的串按字典序从大到小排序, 求排序后的第 $k$ 个串.
$n, m\le 1000, k\le 10^18$
考虑二分字典序, 现在求大于一个串 $t$ 的划分方案数.
显然为了满足 $m$ 和大于的条件, 考虑记录 $f_{i, j}$ 表示 $[1, i]$ 划分 $j$ 段的方案数, 那么此时有
$$
f_{i, j}=\sum f_{k, j-1}, \ s. t. \ s[k+1, i]>t
$$
此时转移是 $n^3$ 的, 因为我们找不到转移到性质–字典序更多取决于开头的 $k$ 而不是 $i$ , 所以同一个 $i$ 的决策看不到性质.
那么考虑倒着dp, 记录最后一段 $[i, n]$ 的, 此时转移的是一个后缀, 就直接做了.
看看lyh的解法, 考虑正着dp的时候一个 $j$ 可以转移到一个后缀的 $i$ , 于是用转移 $f_{i, j-1}\to f_{i, j}$ , $f_{i-1, j-1}\to f_{i, to_j}$ 做到这个转移.
[think] 可以感受到dp的自动机特性, lyh的解法相当于做了前缀优化建图. 适用于前后缀(因为自动机不能记忆你是什么时候开始的区间).
CF1270F Awesome Substrings
给定 $s, s_i\in {0, 1}$ , 求它有多少个子串满足其长度为1个数的倍数.
$\vert s\vert \le 2\times 10^5$
倍数一般与某些自然根号, 对数性质有关.
考虑一个经典做法是对于一个固定倍数 $k$ , 把 $0$ 当成 $-1$ , 1当成 $k$ , 有解就是区间和为0, 可以扫一遍得答案. 那么此时想到根号分治, 这个用于 $k<\sqrt n$ .
对于 $k>\sqrt n$ , 则 $1$ 的个数要小于根号, 于是枚举小于根号的1的个数就行了.
CF1270H Number of Components
给一个长度为 $n$ 的数组 $a$ , $a$ 中的元素两两不同.
对于每个数对 $(i, j)(i<j)$ , 若 $a_i<a_j$ , 则让 $i$ 向 $j$ 连一条边. 求图中连通块个数.
支持 $q$ 次修改数组某个位置的值, 每次修改后输出图中连通块个数.
$n, q\le 5\times 10^5, 1\le a_i\le 10^6$ , 保证任意时刻数组中元素两两不同.
首先考虑连通块的性质, 发现若 $i, j(i<j)$ 连通, 则任意 $k\in [i, j]$ 都连通, 于是一个连通块一定是一个区间.
于是问题变成有多少个 $i$ 满足 $\min_{j\in [1, i]} a_j>\max_{j\in [i+1, n]} a_j$
考虑一个折线模型, 发现 $i$ 满足条件代表 $y=a_i-\dfrac{1}{2}$ 这条线与整个折现只有一个交点, 发现我们成功的把修改时信息的影响变得局部–折现只与它左右两边的元素有关, 于是用值域线段树维护每个位置被折现覆盖了多少次的最小值何最小值个数(或者, $y=x$ 与多少条折现经过), 修改就是区间加了.
CF1260F Colored Tree
给定一棵树, 每个节点有一个颜色 $h$ , $h_i$ 为 $[L_i, R_i]$ 内的一个整数.
现在, 对于所有 $\prod (R_i-L_i+1)$ 种不同的染色方案, 求出下列式子之和:
$$\sum_{h_i=h_j, 1\leq i<j\leq n}dis(i, j)$$
$n\leq 10^5, 1\leq L_i\leq R_i\leq 10^5$ , 答案对1e9+7取模.
能不能拆成边的贡献啊. . . 一条边的贡献为每种颜色 所有方案下在两边的个数乘起来 之和, 然后呢?
那再考虑对每个颜色分别求, 这个好像可以虚树实现.
于是问题变成求一个颜色在一个子树内的所有出现方案的出现点数之和.
考虑写成 $a+x$ 卷起来, 要求系数和次数的点积. 那是不是求导把次数移下来就好了. 所以是问在1处的导数.
这个是可以做的, $(\prod_i a_i)’=\sum_i (a_i’\prod_{j\ne i}a_j)$ , 于是就是在这个区间里选一个的贡献是导数, 剩下的是原来的, 这个问题是可合并的, 或者从ddp上想. 于是可以单点修改/查子树.
设 $R_i-L_i=l_i$ .
诶好像建虚树是错的啊. . . 复杂度假了. . . 但上面那部分是对的, 再想想, 考虑扫描线颜色维(这里颜色实际是有大小关系的), 设每个边两边的这种颜色的所有方案的出现点数之和分别是 $A, B$ , 那么 $A\times B$ 就是这条边的贡献, 那么现在扫着扫着要支持添加一个点或删除一个点, 发现按照刚才的做法求导之后 $A=\sum_i \prod_{j\ne i}l_j$ , 就要求 $(\sum_i \prod_{j\ne i} l_j)\times (\sum_k \prod_{l\ne k}l_k)$ , 发现添加一项不是线性变换, 但可以直接两边都除以 $\prod_i l_i$ , 这个对所有点是相同的提出来, 就成了 $(\sum_i \dfrac{1}{l_i})(\sum_j \dfrac{1}{l_j})$ , 就是线性变换了.
然后写成矩阵, 发现行列式恒为1, 于是是可逆的, 就支持加点删点了, 用线段树维护dfs序, 复杂度1log.
这个题还有其他做法啊: 好像大家都是考虑的点对贡献而不是边.
于是点对 $u, v$ 贡献就是
$$
dis(u, v)\times \dfrac{all}{l_ul_v}
$$
然后依旧扫描线, 这次用点分树维护跨过根的即可.
CF1254D Tree Queries
给定一棵 $N$ 个节点的树, 有 $Q$ 次操作
$1\space v\space d$ 给定一个点 $v$ 和一个权值 $d$ , 等概率地选择一个点 $r$ , 对每一个点 $u$ , 若 $v$ 在 $u$ 到 $r$ 的路径上, 则 $u$ 的权值加上 $d$ (权值一开始为 $0$ )
$2\space v$ 查询 $v$ 的权值期望, 对 $998244353$ 取模
$1\leqslant N, Q \leqslant 150000$
固定 $r$ , $v$ 决定了加到子树的哪一边. 好像很不可做.
固定 $u, v$ 考虑被加了几次, 显然是 $dis(u, v)$ , 问题就成了每次给 $u$ 加上 $dis(u, v)*d$ , 单点询问.
那么这个很经典啊, 点分树+线段树. 等等, 看成给 $r$ 到 $v$ 的路径上了加.
再看看, 是给 $v$ 子树外的点加子树大小次, 自己加 $nd$ 次, 关键是子树内的点, 每个被加了子树大小减自己所在的子树的大小.
最后这块不好办, 考虑树上差分, 并且每个位置维护子树被加了几次, 就是要给 $v$ 子树加1, 每个儿子这个次数减1, 上科技的做法是毛毛虫剖分
考虑一个阳间做法, 树剖, 每次修改的时候给重儿子区间加, 对于轻儿子, 跳它祖先上每一条轻边算贡献即可.
CF1223F Stack Exterminable Arrays
收录在dp里.
CF1220F Gardener Alex
给定排列 $p_n$ , 可以进行 $k$ 次向左循环移位, 问大根笛卡尔树深度的最小值以及循环移位次数
$n\le 2\times 10^5$
考虑动态的做: 每次从左边拿一个到右边叫 $u$ , 则原来 $u$ 的右儿子挂到 $u$ 左边第一个大于它的, 新的父亲是它左边第一个大于它的点 $v$ , 小于 $v$ 的没有影响, $[v, u]$ 之间的点挂到了 $u$ 的左子树且结构不变. 现在可以LCT+线段树1log.
考虑不LCT, 而是变成每个位置维护其深度, 是不是就做完了.
CF1188D Make Equal
给出 $n$ 个数字 $a_1 , a_2 , \ldots , a_n$ , 每次操作可以给其中一个数加上 $2$ 的非负整数次幂. 求最少的操作次数, 使得这 $n$ 个数相等.
$n\le 10^5, a_i\le 10^17$
考虑不能直接dp, 因为进不进位是乱的, 因为只能加不能减, 发现最优策略一定是, 先操作最大值, 然后把所有数操作到同一个数, 设 $ma=\max_i a_i$ , 则要最小化 $\sum_i \mathrm{popcount}(ma+x-a_i)$ , 所以设 $b_i=ma-a_i$ , 就是让它们加同一个 $x$ 了.
考虑此时再dp, 仍然要进位, 但因为都是加上同一个数, 所以进位到第 $k+1$ 位的只能是前 $k$ 位最大的那些数, , 设 $f_{i, j}$ 表示前 $i$ 位, 进位的是最大的 $j$ 个, 就可以了.
[trick] 加同一个数时进位的一定是一个后缀, 同CF1322B.
[think] 是构造了满足某条件(这里的进位)的一个偏序关系去压缩状态.
CF1142D Foreigner
给定数字串 $s$ , 求其中有多少子串表示的数是特殊的. 定义特殊的数是 $[1, 9]$ 的数, 或者对于 $k= \lfloor \dfrac{x}{10} \rfloor$ , $k$ 是第 $i$ 个特殊的数, 则要求 $x\bmod 10<k\bmod 11$ .
$n\le 10^5$
考虑在序列上扫, 维护以 $i$ 结尾的特殊的数, 那么显然它们必须在第 $i-1$ 位结尾时也特殊, 并且第 $i$ 位要小于它们的编号, 发现我们并不需要维护每一个特殊的数–编号膜11相同的对后面贡献相同, 所以 $f_{i, j}$ 表示以第 $i$ 位结尾, 编号膜11余 $j$ 的数的个数, 我们希望知道 $j$ 这一维怎么转移.
发现我们需要算编号为 $a$ 的数往后加上数 $b$ (这个操作起名拓展)后的新编号, 考虑由 $c<a$ 拓展得到的数一定都小于 $a$ 拓展得到的, 于是新编号就是
$$
9+\sum_{j\in [1, k-1]} (i\bmod 11)+c+1
$$
意思是算上不是被拓展的9个数, 以及比 $k$ 小的拓展的所有数. 发现 $i$ 每11个加的数是一样的(是 $0+1+2+\ldots+10=55\equiv 0 \pmod 11$ ), 于是我们确实可以像上面一样只记录余数转移了.
CF1129D Isolation
给出一个长度为 $n$ 的序列, 把它划分成若干段, 使得每一段中出现过恰好一次的元素个数 $\le k$ , 求方案数对 $998244353$ 取模后的结果.
$n\le 10^5$
设 $f_i$ 表示前 $i$ 个的方案数, 转移就是枚举最后一段断在哪, 是 $n^2$ 的.
于是优化这个, 考虑维护 $cnt_j$ 表示区间 $[j, i]$ 这一段恰好出现一次的数的个数, 那么现在加入一个位置 $i+1$ 后, 发现若设最大的 $k$ 满足 $a_k=a_{i+}$ , 则 $[k, i+1]$ 的 $cnt$ 加 $1$ , $[1, k]$ 的 $cnt$ 减 $1$ , 然后求 $cnt$ 大于一个数的 $f$ 的和, 可以时间分块+根号平衡, 或者直接序列分块.
CF1098D Eels
小V有一个水缸和一堆鱼, 水缸初始是空的, 小V接下来会向水缸内加入一些鱼, 同时也可能将已加入的鱼捞出来.
水缸里的鱼会相互攻击, 直到只有一条鱼为止. 也就是说如果有 $n$ 条鱼, 则会发生 $n-1$ 次攻击. 如果一条鱼的重量为 $A$ , 另一条鱼重量为 $B$ , 如果 $A\le B$ , 则 $B$ 鱼会吃掉 $A$ 鱼, 然后 $B$ 鱼体重变为 $A+B$ .
对于一场攻击来说, 如果一条鱼的重量为 $A$ , 另一条鱼重量为 $B$ , 如果 $A, B$ 满足条件 : $A\le B$ 而且 $B\le 2A$ 那么我们定义这场攻击是危险的.
现在小V会有 $q$ 次操作, 包括加入一条体重为 $x$ 的鱼, 或捞出一条水缸内的、体重为 $x$ 的鱼.
小V想知道, 在每次操作后, 水缸内能发生的最多的危险攻击次数是多少.$q\le 500000$
考虑一次询问怎么做? (好像不会啊. . . )
首先发现能现在危险的一定可以不拖到以后, 所以你先尽可能合并危险的.
直到现在任意两个鱼打都不是危险的, 发现此时最多有 $\log v$ 条.
发现不会.
考虑猜一个更厉害的结论, 一定每次拿最小的两个合并.
那么如果此时最小的 $a, b$ 是危险的你就直接合并, 现在发现 $a<2b$ , 那么假设此时合并 $bc, c>b$ 是危险的, 发现首先 $a$ 和后面的合并永远不是危险的了, 并且把 $a$ 先合并到 $b$ 上一定不劣, 就证完了.
于是考虑维护一个有序的数字, 答案就是 $a_i\le s_{i-1}$ 的 $i$ 个数, 其中 $s$ 为前缀和.
考虑不合法的合并只有 $\log V$ 次, 那么开个平衡树, 每个位置维护当前值减前缀和, 就要做到插入, 后缀加, 查询大于0的数的个数, 很遗憾这个做不了, 但是可以查区间最小值是简单的, 因为只有 $\log V$ 次每次往后跳复杂度是对的(finger search 1log! )
啊, 不对, fingersearch是2log的
看看题解的高妙做法, 根据权值划分段, $[2^i, 2^{i+1})$ 作为一段, 每一段只有最小的可能不是危险的, 直接维护和就做完了.
CF1044F DFS
给定 $T=Tree(n), G=Graph(n)=T$ , $q$ 次每次在 $G$ 中加一条边或删一条边, 不会删 $T$ 中的边, 问 $G$ 中有几个点满足从这里开始dfs有可能得到dfs树为 $T$ .
$n, q\le 2\times 10^5$
考虑一次怎么做.
那么要求, 若点 $u$ 在 $T$ 上是叶子, 你在图上走到 $u$ 的时候它的相邻点都走过了. 然后发现除了 $u$ 的其他 $fa_u$ 的相邻点应该都走过了这样的.
这样会在树上建一个DAG, 边数是线性的, 问一个点能不能走一个路满足这个先后关系, 好像完全不可做.
[think] 考虑单个操作的简单影响而不是全体操作复杂的限制.
发现对于一条非树边 $u\to v$ , 相当于让链 $u$ , $v$ 之间的点以及它们的子树全不行了, 发现也就是只有 $u, v$ 和链不同向的子树满足条件, 就直接区间加全局最小值个数.
CF917C Pollywog
$n$ 个位置编号 $1\ldots n$ , $x$ 只青蛙, 开始在最左侧的 $x$ 个位置上, 每一秒最左侧的青蛙向右跳, 位于石头 $i$ 的青蛙可以跳跃到 $[i+1, i+k]$ , 体力花费为 $c_1\ldots c_k$ , 不能有两个青蛙在同一位置.
另有 $q$ 个石头是特殊的, 若一个青蛙是特殊的, 则会额外花费 $p$ 的体力.
求它们跳到最右边的 $x$ 个石头的最小代价.
$x\le k\le 8, n\le 10^{18}, q\le \min(25, n-x)$
状压dp.
压缩 $f_{i, S}$ 表示最靠前的青蛙在 $i$ , 其中 $[i-7, i]$ 是否有青蛙的状态是 $S$ .
然后想到矩阵快速幂, 矩阵大小256*256, 那么预处理 $2^k$ 次转移的矩阵, 特殊点分成若干段, 每次用矩阵乘向量优化?
然而发现预处理已经上天了, 矩阵太慢了.
但倍增的思路一定是对的, 考虑设 $g_{i, S_1, S_2}$ 表示 $S_1$ 转移 $i$ 次到 $S_2$ 的代价, 发现可以倍增 $g$ , 转移 $f$ , 但这个和矩阵显然本质相同啊, 复杂度也没变.
不会了, 看lyh题解, 就是这个倍增dp, 只能用常数小解释了.
不过其实是可以优化到能过的范围的, 考虑实际上 $\vert S\vert=n$ , 所以矩阵大小不是 $2^k$ 而是 $\binom{n}{k}$ , 最大是 $\binom{8}{4}=70$ ! . 就无敌了.
刷糊完了lyh的一个课件!
Day6-slide. pdf
数数题默认膜998244353.
CF1408G Clusterization Counting
给定 $n$ 点带权无向联通图, 求把其划分成 $k$ 个不交的组的方案, 满足任意 $s, f, x, y$ 中若 $s, f, x$ 同组, $y$ 与 $x$ 不同组, 则 $w_{x, y}>w_{s, f}$
对 $1\ldots n$ 的每个 $k$ 输出答案.
$n\le 1500$
考虑这个限制的实际含义是组内边大于组间边(然后用形式化题意恶心人).
于是考虑直接按边权递增加边, 相同边权一起加, 那么每个组必然是出现过的连通块.
考虑连通块的总个数, 发现若形成新的连通块必然要加入新点和已有合并, 只有 $O(n)$ 个.
于是把 $O(n)$ 个连通块的包含关系建树, 那么问题就成了在树上选 $k$ 个没有祖先关系的点的方案数.
考虑dp, $f_{u, i}$ 表示 $u$ 子树内选了 $k$ 个即可.
[think] 把限制变成更实际意义的形式理解
[think] 不交的关系在包含关系的树上(父亲代表的集合包含儿子)表示为树上没有祖先关系.
CF1383E Strange Operation
有一个长度为 $n$ 的 $01$ 串 $s$ , 可以对该串进行若干次操作, 每次操作可以将两个相邻的数字合并为两者的最大值(操作之后字符串长度减少 $1$ ). 问操作后有多少种可能的字符串.
$n \le 10^6$
考虑合并操作实质是让一个连续0段或1段缩短一个, 但1段不会消失, 0段有可能消失.
那么考虑判定串 $t$ 可以被 $s$ 得到, 从头开始扫, 如果当前0段长度大于 $s$ 的0段, 那么认为 $s$ 的这个段被消没了接着往下匹配, 如果当前1段大于 $s$ 的1段, 那么认为下一个0段被消没了打通到下一个, 这么贪心的匹配.
那么考虑dp方案, 用dpofdp的思想, 内层状态只需要记录 $t$ 是0/1段, 长多少和 $s$ 的一段长多少, 显然是过不了的.
毫无用处.
看题解, 它用 $a_i$ 表示 $s$ 第 $i$ 个1和第 $i+1$ 个1之间0的个数, 认为可以得到叫包含, 则设 $f_i$ 表示 $a_1\ldots a_i$ 能够, 而更小的前缀无法包含的序列个数. 假设能包含的序列最后一项是 $x$ , 那 $x$ 肯定被 $a_i$ 包含, 考虑如果上一项被 $a_j$ 包含, 那么 $i, j$ 之间的 $a_k$ 都要小于 $x$ 不然就能被更短的包含了. 于是要找到最大的 $a_k\ge x$ 的 $k$ , 贡献到每个位置的 $k$ 是一个 $a$ 上从 $i$ 开始的后缀max, 容易发现每个 $k$ 只能贡献到一个 $i$(因为 $k<i$, 后面由 $i$ 贡献), 可以单调栈做.
然后再处理点边界, 如果 $s$ 只有0是简单的, 并且假设 $s$ 最后最前分别有 $x, y$ 个0, 那么可以把它们剥去, 最后乘上 $(x+1)(y+1)$ , 用两边都是1的做.
[think] 感觉就是, 当我们不知道如何数数的时候, 可以思考一个状态数 $O(1)$ 的判定($t$ 当前前缀最少被 $a_k$ 包含), 把它塞到dp里. 其实就是dpofdp
CF1372E Omkar and Last Floor
给一个 $n\times m$ 的网格, 每一行被分成若干块, 要把格子里填满0/1, 每个块内仅有一个1, 最大化 $\sum {q_i}^2$ , 其中 $q_i$ 为第 $i$ 咧的元素和.
$n, m\le 100$
考虑一定会让最多的列填满.
那么至少让一列填满. 填满的这一列可以把它分成两半, 每一半结论相同.
那么区间dp, 设 $f_{l, r}$ 表示 $[l, r]$ 完整包含的块的答案, 那么枚举一个满的列分成两边就行了. 注意只要完整包含是因为如果没有完整包含一定在其他地方有了1.
CF1366G Construct the String
给定一个包含小写字母和 $\texttt{. }$ 的串 $s$ , 字符 $\texttt{. }$ 表示backspace, 按顺序按下这些按键, 空串再删会崩溃, 求删除最少的字符使得结果为 $t$ 且不崩溃.
$\vert t\vert\le \vert s\vert \le 10^4$
$f_{i, j}$ 表示 $s$ 的前 $i$ 个, 匹配 $t$ 的前 $j$ 个都最小代价. 不会转移.
设 $f_{i, j}$ 表示前 $i$ 个删 $j$ 个得到 $t$ 的最长长度, 也不会转移.
哦第一个是可以转移的啊. 考虑如果一个区间如果执行完是空的, 那么就可以从这个区间前转移, 因为删这个区间中某个不是. 的东西等价于直接在前面删, 删这个区间中的. 相当于保留区间最前面的元素, 相当于把最后一个. 删了, 于是 $f_{i, j}$ 可以由 $f_{i-1, j-1}, f_{i, j-1}, f_{p, j}(\vert f(p+1, j)\vert =0)$ 转移过来, 预处理每个位置从哪里转移过来是简单的.
[think] . 的删除我们是会做的, 不会做的是. 生效, 于是把不删调整成跳过一段转移过来.
CF1342F Make It Ascending
给一个长度为 $n$ 的序列 $a$ , 你可以若干次选择 $i\ne j$ , 让 $a_j: =a_j+a_i$ 并删除 $a_i$ , 用尽可能少的操作将序列变成严格增.
$n\le 15$
$n\le 15$ , 但没有那么高妙, 只要猜状态.
考虑题目是要你选若干个集合, 和递增, 且每个集合选择其中的一个元素的位置递增, 且选的集合尽量多.
那你就设 $f_{S, i, j}$ 已经选了集合 $S$ , 已经选了 $i$ 个集合, 然后最后一个集合的元素的位置是 $j$ 的情况下最后一个集合的和的最小值.
状态好像挺自然? 小于20的dp要使劲设!
[think] upd: 隔一年来看不会做了. . . 直接dp满足条件的终态而非考虑过程
CF1326F2 Wise Men (Hard Version)
给定一个 $n$ 个点的无向图, 对于一个排列 $p_n$ , 对应一个 $01$ 序列 $a_{n-1}$ , 其中 $a_i$ 表示 $p_i$ 和 $p_{i+1}$ 之间是否有边, 给出图, 求对于每个01序列对应多少排列.
$n\le 18$
居然是容斥题.
考虑限制是第 $i$ 位为1或无所谓, 求方案数, 那么只要容斥就能得到答案了. 把这个得到的用FMT可以得到答案.
那么现在一个限制串 $s$ , $s_i$ 为1表示这一位必须为1, 否则任意, 那么其中的0将1分成若干段, 每一段内必须有边, 段间随便走.
那么每一段的大小加一(长 $k$ 的段决定排列中长 $k+1$ 的区间中路径必须都走有边的)构成的可重集相同的 $s$ 答案相同. 原因是考虑: 段间不做要求所以两个段可以任意互换.
于是对每个可重集求答案. 因为可重集总和是 $n$ , 所以只有18的划分数大概不到400种情况.
那么处理长度为 $i$ , 走过 $S$ 中点的方案数 $g_{i, S}$ , 要求的 $f$ 是若干个 $g$ 的卷积, 要满足 $S$ 的并是全集, 并且对应的大小是 $i$ . 那就对每个划分卷一遍就行了. 复杂度 $385\times 2^n+2^nn^2$ .
[think] 容斥放宽限制
[think] 计数问题找等价类(这里的 $S$)

CF1290F Making Shapes
给定 $n$ 个向量, 你可以把它们接起来走回原点得到多边形, 求这个多边形是凸的且可以被 $m\times m$ 的矩形框住的方案数. 不同位置的凸多边形算不同的.
$n\le 5, m\le 10^9, x_i, y_i\in [-4, 4]$
考虑实际上多边形的形状仅取决于每种向量的个数, 因为凸多边形意味着我们对向量极角排序.
于是问题变成确定每组向量个数使得它们两个方向上和为0. 设个数分别是 $c_1, c_2, \ldots, c_n$
这个东西很难做, 因为它们的数量实在太大. 考虑逐位确定个数, 设 $f_{i, x_pos, x_neg, y_pos, y_neg, 0/1, 0/1}$ 表示 $c$ 的前 $i$ 位确定时, $x, y$ 的正负部分的进位和正负部分和的前 $i$ 位是否等于 $m$ 的前 $i$ 位的方案数, 每次枚举 $n$ 个 $c$ 在下一位是0/1的 $2^n$ 种情况.
[think] 逐位确定个数, 用类似数位dp的方法设计状态, 用在值域大, 且我们关心的性质相对简单(比如这里只是大小关系)
CF1299D Around the World
等好好学线性基, 考虑dp, 则 $t$ 要么包含 $s$ 作为子串, 要么它的前缀是 $s$ 的后缀, 它的后缀是 $s$ 的前缀.
CF1292F Nora’s Toy Boxes
$m$ 个不同正整数 $a_m$ , 每次选择不同的 $i, j, k$ 满足 $a_i$ 整除 $a_j, a_k$ , 然后删掉 $a_k$ , 求不同的最长的删除序列数.
$m\le 60, a_i\le 60$
关系建图, $ka_i=a_j$ 则 $a_i\to a_j$ , 图有很多个来连通块, 每个是独立的. 现在可以只考虑一个连通块.
于是每次可以选一条边, 然后在起点连出去一个点.
考虑这是个偏序图, 所以所有点都由连通块没有入度的点直接相连, 并且因为它是一个连通块, 所以只要有一个数就能拓展出, 所以只要保留一个数就可以拓展出其他所有的.
[think] 关系建图辅助思考
[think] 删/加转化
再考虑计数重建的过程, 能加入点 $a$ 需要存在 $b$ 能与其有共同因数是根, 所以设 $f_{S}$ 表示连向加入的点的根的集合是 $S$ , 那么新的点的集合必然要与 $S$ 有交集并且没有加入过, 发现不会判断没有加入过这个条件. 发现如果新的点的质因子集合 $T$ 不被 $S$ 包含肯定没加入, 否则我们可以再加一维表示已经加入的点数, 此时知道被 $S$ 包含的总点数和已经加入的点数, 于是知道还没加入的点数, 那么从这里面挑一个转移就也能做了. 复杂度是 $2^r\times (n-r)^2$ , 其中 $r$ 是根的个数.
[think] 我们不知道某个性质的东西, 但可以知道它们的总数, 那么数数的话有的时候只要知道总数就能转移了.
考虑如果一个根超过 $\dfrac{n}{2}$ , 显然连不到任何东西是孤立点, 现在考虑小于 $\dfrac{n}{2}$ 的互不包含的数, 发现只考虑质因数2(删去所有质因数2后的不同数个数)就已经能分析到 $r<\dfrac{n}{4}$ , 所以可以过.
CF1286F Harry The Potter
假设有一个包含 $n$ 个元素的数组 $a$ , 现在需要把此数组的每个元素都变为 $0$ .
可以进行的操作有:
- 选定两个数 $i$ 和 $x$ , 然后把 $a_i$ 减去 $x$ . (注意, $x$ 可以是负数)
- 选定三个数 $i, j$ 和 $x$ , 然后把 $a_i$ 减去 $x$ , 把 $a_j$ 减去 $x+1$ .
请输出最少的操作次数.$\vert a_i\vert \le 10^{15}, n\le 20$
完全不会.
考虑用2类操作节省必须是 $k-1$ 步干掉 $k$ 个数, 所以是划分若干集合, 每个集合用2操作 $k-1$ 步删完, 剩下的用操作1.
[think] 用不弱的操作等效替换. 通过极大, 极小的性质简化(这里要求集合是极小的才有这个性质).
每个集合内的从左可以形成一棵树(边是 $k-1$ 个操作, 点是 $k$ 个数, 又要连通, 显然不能有环). 树是二分图, 可以将点分到两边, 发现每一步是将两边的差改变1并将一个数变成0. 于是差最多变化 $\vert S\vert-1$, 于是能不能节省的条件就是差在这个范围内并且差的奇偶性与 $\vert S\vert -1$ 一样. 于是现在判定一个集合就是要找到左右两边.
[think] 博弈论, 操作这类的抽取关键特征(左右两边的差)证充要.
那么判定一个集合这件事用meet in the middle是简单的, 现在要判定所有集合, 那么直接暴力是
$$
\sum \binom{n}{i} \cdot 2^{(\dfrac{i}{2})}=(1+\sqrt 2)^n
$$
没问题.
最后就是dp, $f_S$ 表示 $S$ 能找出多少个这样的集合, 可以或者 $3^n$ dp.
说是可以子集卷积, 但是我不会啊.
CF1279F New Year and Handle Change
- 给出一个01串(表现为大小写), 可以最多选择 $k$ 个 $l$ 长度的子串, 全部变为0或1.
- 求操作后的 $\min(cnt_0 , cnt_1)$ 的最小值
- $1 \le n, k, l \le 10^6$
感觉 $10^6$ 很难做, 而且我们会不限次数的版本($f_i$ 表示前 $i$ 个的最小值, 直接转移), 所以想一想得干掉 $k$ 这一维.
感觉能用的方法只有wqs二分. 显然收益是递减的, 否则可以把收益更大的放到前面做. 于是做完了.
CF1276D Tree Elimination
给定一棵 $n$ 个点的树, 点编号 $1 \sim n$, 第 $i$ 条边连接 $a_i$ 和 $b_i$.
初始时你有一个空的序列, 树上的 $n$ 个点都有标记.
现在按照边的编号从小到大考虑每一条边:
- 如果这一条边连接的两个点都有标记, 则选择其中的一个点, 擦除它的标记并将它的编号放入序列的末端;
- 否则什么都不做.
求能够由上述操作得到的不同的序列数量 $\bmod\ 998244353$.$n\le 2\times 10^5$
不同的序列就是不同的消除编号方案.
从边权维考虑很扯, 并且因为限制相对局部, 只能从树这一维去做.
对于一个点的方案, 一个点向上转移时我们只需要知道这个点和父亲见面的那次结果. 考虑把出边权值排序, 设 $f_{u, 0/1/2/3}$ 表示 $u$ 没被删掉/在遇到父亲前被删掉/遇到父亲时被删掉/遇到父亲之后被删掉.
$f_{u, 1/3}$ 转移是考虑枚举这个点被哪个儿子干掉了, 那么这个儿子前的儿子只能选 $1, 2$, 干掉父亲的儿子可以选 $0, 3$, 后面的只能选 $0, 1, 3$. 懂了这个其他的就显然了.
[think] 枚举树上扫描线方向, 有些问题(比如这个)看起来是序列维的(比如这里从小到大插入边), 但实际上树上一个点邻边是一个局部的东西, 所以可能仍然是树这一维.
CF1225G To Make 1
给定 $a_n$ 和 $k$, 保证 $k\not{\vert}\ a_i$, 每次可以选择 $x, y$ 删除并加入新的数 $f(x+y)$, 其中
$$
f(x)=
\begin{cases}
f(\dfrac{x}{k}), k\vert x\
x, otherwise
\end{cases}
$$
问最后能不能只剩下 $1$. 构造方案.
$n\le 16, k\le 2000, \sum a_i\le 2000$
$f_{S, i}$ 表示 $S$ 中集合凑出 $i$ 是否可行. 转移的时候删掉一个拼过来, 复杂度是 $2^nnv^2$
不会了. 考虑每个数对总答案的贡献是 $\dfrac{a_i}{k^{p_i}}$, 显然如果有这样一组 $p_i$ 使得和为1, 那么一定可以找到答案, 只要每次选择最大的两个合起来即可.
那么考虑找到 $p$ 的方式, 模拟 $p$ 的形成过程, 也就是一开始找到若干数的和是 $k$ 的倍数, 合并并给它们 $p$ 加1, 不断重复, 于是类比模拟设计dp, $f_{S, i}$ 表示集合 $S$ 中数的贡献和是 $i$, 转移是除以 $k$ 或者新加一个数, 复杂度是 $2^nnv$(真的能过啊算一算, 不过bitset优化到 $\dfrac{1}{w}$).
[think] 考虑一个数经过若干操作后对答案的贡献, 通过一组合法贡献构造策略.
[think] 把一个策略形成过程的几种操作作为dp的转移设计dp, 比如这里的 $p$
CF1197F Coloring Game
- 有 $n$ 条纸条, 第 $i$ 个纸条被分成了 $a_i$ 个格子, 编号从 $1$ 到 $a_i$, 最开始每个格子是 $3$ 种颜色中的一种.
- 游戏开始时, 有 $n$ 个棋子放在每个纸条的第 $a_i$ 个格子(即最后一个格子). 然后两个玩家进行轮流操作, 先不能操作者输.
- 每次操作选择一枚棋子, 向后移动 $1, 2$ 或 $3$ 格. 要求棋子不能越过纸条的边界, 且若要从颜色为 $i$ 的格子向前移动 $j$ 个格子必须满足 $f_{i, j}=1$.
- 现在有些格子是未进行过染色的, 问有多少种染这些格子的方案, 使得后手有必胜策略, 对 $998244353$ 取模.
$1\le a_i\le10^9$, $1\le m\le 1000$, $1\le x_i\le n$, $1\le y_i\le a_{x_i}$, $1\le c_i\le 3$, $0\le f_{i, j}\le1$.
先考虑单个纸条算SG, 因为一个位置只能移动到往后三个位置, 所以SG值最多是3.
一个dp说 $f_{i, j}$ 表示第 $i$ 个格子颜色为 $j$ 的SG值, 那么dpofdp说 $f_{i, j, k}$ 表示第 $i$ 个格子, 颜色为 $j$, SG值为 $k$ 的方案数. 这个东西仍然性质很局部, 写成矩阵就冲了.
CF1194G Another Meme Problem
定义一个分数 $\dfrac{y}{x}$ 是好的当且仅当其等于某个 $\dfrac{x’}{y’}$, ($x’, y’\in [1, 9]$), 其中 $x’, y’$ 分别出现在 $x, y$ 的十进制表示中. 求有多少 $x, y\le n$ 的分数是好的.
$n\le 10^{100}$. 膜 $998244353$.
首先可能的 $\dfrac{y}{x}$ 的值只有81种. 枚举一个 $(x’, y’)$ 计算.
于是要求 $x=kx’, y=ky’$, 可以数位dp, 但是有重复的情况, 于是钦定互质, 但那样的话同一个 $x, y$ 可能不满足 $(x’, y’)$ 而满足 $(ax’, ay’)$, 注意到 $a$ 很小(最大是 $9$, 第二大是 $4$), 所以状压dp, 就是 $f_{i, s_1, s_2, 0/1, 0/1, 0/1, 0/1}$ 表示前 $i$ 位, $x, y$ 分别可能的 $a$ 的集合是 $s_1, s_2$, 两者分别的进位, 与 $n$ 的大小关系即可.
这里分析复杂度的话注意不需要具体的 $s_1, s_2$, 而是两者只要包含了相同的 $a$ 之后立刻就没有意义, 所以实际状态数更小一些.
CF1152F2 Neko Rules the Catniverse
欸刚刚杂题里写了.
CF1146H Satanic Panic
给定平面上 $n$ 个点问以5个点为顶点能组成多少五角星, 对边长无要求, 对边的相交方式有要求.
保证无三点共线, $n\le 300$.
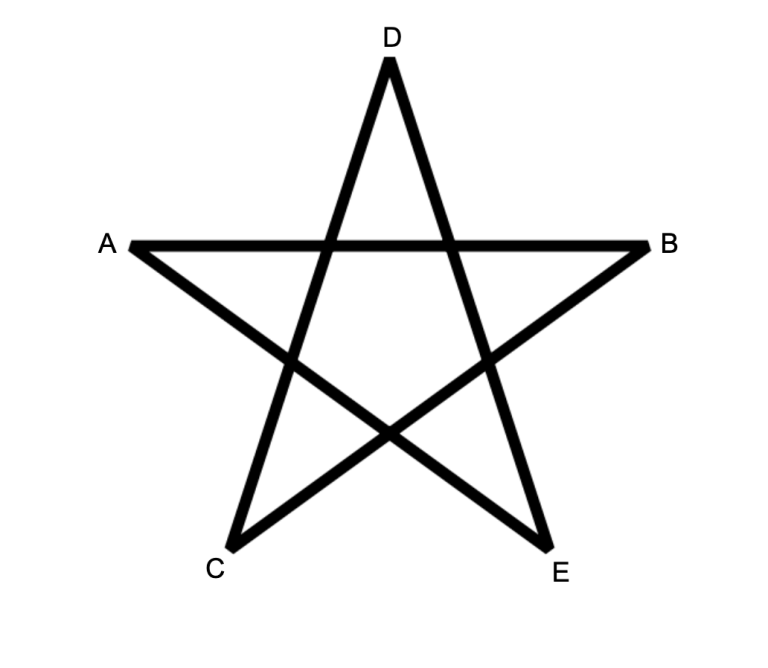
需要先观察一下五角星. 发现是任何一个凸五边形即可.
第一个反应是用点dp, $f_{i, j, k}$ 表示点 $i$ 开始, 第一条边的角度是 $j$, 走 $k$ 条的方案数, 状态数是 $n^3$, 转移的时候要枚举另一个状态就成了 $n^4$. 那如果 $j$ 一维用线段树是不是可以 $n^3\log n$ 啊.
考虑把点对作为对象, 那么可以极角排序, $f_{i, j}$ 表示走了 $i$ 条边走到点 $j$, 再枚举一个起点即可.
注意不会重复计算某个多边形因为极角排序了, 相当于它只会沿着递增的斜率走.
[trick] 在 $n$ 几百的情况下凸多边形的问题可以考虑把点连成边用边做. 这个套路和 P2924 [US ACO08DEC]Largest Fence G 是一样的.
CF1142D Foreigner
slide. pptx里面有了, 讲了两遍啊.
CF1119F Niyaz and Small Degrees
有一个 $n$ 个结点的树, 每条边有边权, 结点度数就是与之相连的边数量. 对于 $0 \le x < n$, 删掉一些边使每个结点的度数不大于 $x$, 求出删掉的边的权值和最小值. 对每个 $x\in [0, n-1]$ 求答案.
$n\le 250000$
先考虑一个确定的 $x$. $f_{u, 0/1}$ 表示 $u$ 的子树内的最少代价, 其中有没有删 $u$ 的父边. 转移考虑先都选 $f_{v, 0}$, 然后把 $f_{v, 1}-f_{v, 0}$ 排序, 把一个前缀删了. 复杂度是 $n\log n$
[trick] 注意只要关心度数大于 $x$ 的点, 发现所有 $x$ 关心的点的个数总和是度数和 $2n-2$.
但暴力转移不对–一个菊花的边就能炸掉.
要让复杂度关于点, 那么考虑关心的点形成若干连通块, 每个连通块分别做, 那么每个点开一个数据结构维护所有已经不敢兴趣的点的边, 如果大小超过要删的个数就干掉最大值, 此时堆内元素和即为叶子答案, 对于每个连通块, 先求连通块的叶子, 然后把答案传给父亲, 将感兴趣的孩子传上来的放到堆里求最小的若干个再复原即可让复杂度和不感兴趣的儿子无关. 数据结构是个堆, 复杂度 $\log n$
CF1103D Professional layer
给定 $1 \le n \le 10^6$ 个正整数 $a_i, 1 \le a_i\le 10^{12}$ , 修改第 $i$ 个正整数 $a_i$ 的花费为 $e_i, 1 \le e_i \le 10^9$ , 以及正整数 $1 \le k \le 10^{12}$ .
要求选出若干个正整数进行一次修改, 使得修改后所有正整数的最大公约数等于 $1$ . 修改操作为: 对于正整数 $a$ , 选择 $a$ 的一个约数 $d \le k$ , 把 $a$ 修改为 $\frac{a}{d}$ .
设选出并修改的正整数有 $x$ 个, 他们的花费之和为 $y$ , 则总的修改花费为 $x \times y$ . 求最小花费.
考虑全局的 $gcd$ 设为 $g$, $g$ 显然最多有 $m=11$ 个不同的质因数. 那么首先其他质因子都等于没有直接杀了, 此时还剩下 $M=12000$ 个数(打表算啊). 每种数效果显然是相同的, 那么最多是都从同一种数操作, 所以每一种数只需要保留 $m$ 个数. 那么可以算出这个数消掉每个 $g$ 的质因子的子集的代价, 复杂度 $Mn2^m$.
于是对于每个子集, 我们知道了哪些数可以消掉它, 此时仍然只有前 $m$ 个有用(因为我们最多用 $m$ 个数消完, 所以前 $m$ 个数一定不会全都被其他因子用了).
于是考虑状压dp, $f_{i, j, S}$ 表示前 $i$ 个数字 $c$ 次操作消掉集合 $S$ 的代价, 转移只要枚举 $i$ 对应的子集和与其不相交的 $T$ 即可从 $f_{i-1, c-1, T}\to f_{i, c, T\cup S}$, 复杂度 $m^23^m$
CF1097G Vladislav and a Great Legend
给定 $Tree(n)$, 对于点集 $X$, 设 $f(X)$ 表示至少选多少条边可以使点集联通, 求 $\sum_{X\subseteq {1\ldots n}, X\ne \varnothing} f^k(X)$
$n\le 10^5, k\le 200$
考虑工业化的处理 $f^k(X)$ 而不是在这里试图智慧的处理这个幂, 普通幂对组合意义没有下降幂友好, 斯特林数变成
$$
\begin{gathered}
n^k=\sum_i {k \brace i}n^{\underline{i}}\
\sum f(X)^k=\sum_i {k \brace i}(f(X))^{\underline{f(X)}}\
=\sum_i {k\brace i} i! \sum \binom{f(X)}{i}
\end{gathered}
$$
前面那部分不用管了, 组合意义说后面相当于对于每个虚树选 $i$ 条边的方案数之和. 要 $nk$ 算所有的.
考虑dp, $f_{u, i}$ 表示 $u$ 的子树内选 $i$ 条边的答案. 其中一条边被选了要求它下方的子树有点在 $X$ 中被选. 再设 $g$ 是多考虑了父边. 那么 $f$ 的转移是先合并所有子节点的 $g$, 而 $g_{u, i}=f_{u, i}+f_{u, i+1}$(关于上面那条边选不选). 因为每次都要考虑当前节点选不选, 所以 $u$ 合并儿子的时候初始状态是 $f_{u, 0}=2$. $g_{u, 1}$ 要减1表示子树内并没有点但你选了个父边.
对于统计答案, 钦定在一个虚树的根统计这个虚树, 那么不是根的情况就是所有的全来自同一子树, 其他点和根都没选, 此时减去 $g_{v, i}$.
总复杂度 $k^2+nk$.
CF1085G Beautiful Matrix
一个矩阵是漂亮的当且仅当其中只包含 $1\ldots n$ 的正整数, 每行元素互不相同, 每个上下相邻的元素不相同. 给定漂亮的矩阵 $A$ 问这个矩阵在所有的漂亮矩阵中的字典序(从0开始). 字典序是从上到下逐行比较.
$n\le 2000$
那肯定是计数有多少个矩阵字典序小于当前矩阵, 因为是字典序所以只要钦定第一个小于 $A$ 的位置就是不重不漏. 再考虑所有漂亮矩阵的方案数是 $n! \cdot {D_n}^{n-1}, D_n$ 为错排数. 那么假设钦定了 $i, j$ 是第一个小于的, 问题就变成了这一行 $j$ 之后有多少种方案. 发现这个方案数只和有多少数在前面出现了有关(因为是等价的, 可以认为是 $k$ 个位置 $a_i\ne i$ 的排列), 若 $A_{i-1, j+1\ldots n}$ 和 $A_{i, j+1\ldots n}$ 有 $k$ 个数相同, 则这个比它小的也有 $k$ 个相同. 求相同个数是简单的.
于是问题就变成如何求长 $i$ 的序列有 $j$ 个钦定不能的方案数 $f_{i, j}$, 考虑递推, 是 $f_{i, j-1}-f_{i-1, j-1}$(长 $i$ 的限制了 $j$ 位的减去最后一个选了 $n$ 的).
总复杂度是 $n^2\log n$($\log n$ 来自求相同个数的时候用的树状数组).
CF1082F Speed Dial
给定 $n$ 个电话号码 $t_i$, 第 $i$ 个被输入 $m_i$ 次, 你可以设置 $k$ 个串 $s_i$, 每次输入一个电话号码的时候可以选择一个 $s_i$(或者不选), 在其基础上补充完剩下的部分. 最小化输入次数(设置 $k$ 个串的部分不算次数).
$n, \sum t_i\le 500, k\le 10$
因为预先设置的都作为前缀, 考虑建一个trie. 此时问题变成选择 $k$ 个节点, 每次输入的代价是到最近的点的距离.
以子树为扫描线方向去做, 关键问题是如何统计子树内到 $u$ 的贡献. $f_{u, k, i}$ 表示 $u$ 的子树内选了 $k$ 个点, 到 $u$ 的路径上没有选点的权值总和为 $i$. 转移如果 $u$ 选就 $i$ 置为 $0$, 否则就累加起来再加 $1$($u$ 自己). 转移需费用提前计算. 复杂度是爆炸.
不会了, 看看lyh的dp是设 $f_{u, c, d}$ 表示 $u$ 距离上面最近的关键点距离为 $d$, 子树内有 $c$ 个的最小代价. 相当于假定一个关键点计算代价. 感觉与费用提前计算本质相同.
[think] upd: 对于一个子树, 我们不知道的是没有选到关键点的点的代价, 它相当于一个内部外部选点组合的代价 $cost(S, T)$, 一个是内部选点, 一个是外部选点, 内部的方案对贡献本质有 $\sum m$ 种, 而外部只本质有 $n$ 种.
CF1067E Random Forest Rank
给定一棵 $n$ 个节点的树, 每条边有 $\frac{1}{2}$ 的概率出现, 可以得到一个森林, 求这个森林邻接矩阵的秩的期望.
$n\le 5\times 10^5$
好了第一步转化就不会了, 结论是 $rank$ 是最大匹配的两倍. 证明是考虑把这些点对应的行拿出来是原来的一组基且线性独立.
剩下的部分可以想一想, 要对森林的匹配求和. 肯定是子树结构, 想一想最大匹配怎么求, 可以贪心从下往上选, 那么设 $f_{u, 0/1}$ 表示 $u$ 有没有被选的方案数, $g_{u, 0/1}$ 表示答案就能转移.
CF1063F String Journey
给定 $s_n$, 求选出最多不交子串满足出现的位置不相交且一次排列($t_{i+1}$ 在 $t_i$ 之后), 且 $t_{i+1}$ 是 $t_i$ 的真子串. 求最大的 $k$.
$n\le 5\times 10^5$
从后往前, 一定可以每次只添加一个新字符. 同时也能看出来 $k$ 和 $\vert t_k\vert$ 是 $\sqrt n$ 量级.
那么dp的几种可能是, $f_i$ 表示最后 $i$ 个字符最大匹配几个 $t$, 或最后 $i$ 个 $t$ 最少匹配到哪. 第二种不会转移, 第一种可以hashtable维护做到 $n\sqrt n$.
考虑优化: 首先显然相邻两个 $f$ 相差不超过1. 那么可以考虑一个判定来转移, 每次给定 $i, k$ 判断能否 $f_i\ge k$, 从第一个位置开始往下问就可以 $O(n)$. 考虑如何判定, 通过这个可以确定这次的 $t$, 枚举删哪个端点就判定知道上次的 $t$, 那么建SAM, 就是查 $t$ 在 $i-k$ 之前的 $endpos$ 的最大值, 然后直接查那个位置的 $f$ 即可.
CF1060F Shrinking Tree
给定 $Tree(n)$, 每次等概率随机删掉一条边 $u\to v$, 并在边的两个端点随机一个, 把这个点 $u$ 的所有边 $u\to v$ 接到另一个点 $w$ 上变成 $w\to v$, 问每个点被剩下的概率.
$n\le 50$
怎么才2900. . . 好难想的状态. . . 是外国人都这么会DP所以分低吗?
先说解法, $f_{u, i}$ 表示 $u$ 的子树内, 删掉最后 $i$ 条边之前和之后根相同的概率. $g_{u, i}$ 是根是 $u$ 的父亲并且加上 $fa\to u$ 这条边.
那么对于合并 $u$ 的儿子 $v$, 转移分两步:
- 加入 $v$ 父边, 也就是 $f$ 到 $g_{v, j}$, 只要考虑边 $u\to v$ 的加入时间 $i$:
- 如果 $i>j$, 也就是 $i$ 删除时间更早, 那么它的结果不影响(只关心 $j$ 之后的), 直接 $f_{v, i}\to g_{v, j}$
- 如果 $i\le j$, 也就是 $i$ 是 $j$ 之后删除的, 那么为了不影响根要求删它的时候必须选 $v$, 所以 $\dfrac{1}{2}f_{v, i}\to g_{v, j}$
- 合并, 也就是 $g_v$ 到 $f_u$, 枚举最后 $i$ 条中 $g_v$ 中有 $j$ 条, $f$ 中有 $i-j$ 条, 转移是两个隔板法的组合数.
[think] 至于状态设计, 我的理解是考虑到每个点表示原图的一个连通块, 并且根可能移动, 所以设计”根相同”这样离谱的状态, 而最后 $i$ 条是考虑到 $u\to v$ 没删的时候子树 $v$ 内部的顺序不影响 $u$.
最后复杂度是 $n^3$(第一部分前缀和优化, 第二部分树形背包分析).
写了代码, 如果按照概率写(这个题要求输出小数, 这样有精度), $g_v$ 合并到 $f_u$ 这一步, 若最后 $i+j$ 条有 $j$ 条来自 $v$, $i$ 条来自已经合并完的 $u$ 的部分, 那么你的新概率应该是 $g_{v, j}f_{u, i}\cdot \dfrac{\binom{siz_u}{i}\binom{siz_v}{j}}{\binom{siz_u+siz_v}{i+j}}$. 考虑如果求的是方案数, 你不能直接插板: 直接插板不能保证插完了最后 $i+j$ 个里面有 $i$ 个来自 $u$, 你需要前面后面分开插. 同时, 因为 $f_u$ 实际上是 $\dfrac{f’_u}{siz_u! }$, 这个推一下就产生分母上的组合数.
CF1038F Wrap Around
考虑dp, 则 $t$ 要么包含 $s$ 作为子串, 要么它的前缀是 $s$ 的后缀, 它的后缀是 $s$ 的前缀.
设 $f_{i, l, r, p, 0/1}$ 表示 $t$ 的前 $i$ 个字符, $t$ 最长的是 $s$ 子串的前缀对应子串为 $s_{l\ldots r}$, 最长的后缀对应 $s$ 的前缀是 $s_{1\ldots p}$, 是否包含 $s$ 作为子串.
这里这么设是因为, 在往 $t$ 的后面添加字符的情况下, 我们可以容易的确定匹配 $s$ 的前缀, 但不能容易的确定匹配 $s$ 的后缀, 所以第一部分要记录 $l, r$ 而第二部分只记录 $p$. 而 $0/1$ 位的转移更是简单的.
CF995F Cowmpany Cowmpensation
$n$ 个点的有个树, 需要给每个点赋 $[1, D]$ 之间的值, 满足每个点的权值不超过其任意祖先. 问方案数.
$n\le 3000, D\le 10^9$
$f_{u, k}$ 表示这棵子树, 所有点权不超过 $k$ 的方案数, 有 $f_{u, k}=f_{u, k-1}+\prod_v f_{v, k}$, 发现是关于 $k$ 的 $size_u$ 次多项式(归纳可得). 所以拉插.
CF981H K Paths
给定 $Tree(n)$, 找到 $k$ 条有编号的路径, 满足树上每条边只能被 $0/1/k$ 条路径覆盖且至少有一条被 $k$ 条覆盖. 求方案数.
$n, k\le 10^5$
考虑固定了 $u, v$ 为这 $k$ 条路径的交的两个端点, 有两种可能: $u, v$ 有祖先关系, 或者没有.
那么问题就是处理出 $f_u, g_u$ 表示一个端点为 $u$, 另一个端点在 $u$ 子树内/外的方案数, 于是没有祖先关系的直接相乘 $f$, 再给每个点 $u$ 加上 $g_u \sum_{v\in subtree(u)} f_v$. 问题变成如何求 $f, g$.
先考虑 $f$, 注意到不会有两个链延伸到相同的子树, 而在一个子树内显然另一个端点随便选, 所以有 $i$ 条没有停留在点 $u$ 的生成函数就是 $F=\prod_{u\to v} (1+siz_v\cdot x)$, 某个 $i$ 的方案数是 $[x^i]F$, 总方案数就是 $\sum_i k^{\underline{i}}a_i$. 这个复杂度是 $c\log^2 c$, 其中 $c$ 为儿子个数, 因为度数总和是线性所以没问题.
但不会算 $g$, 这个东西复杂度现在和父亲度数有关. 考虑直接带着和答案一起算, 那么设 $G=\sum b_ix^i$ 刚才说的 $g_u \sum_{v\in subtree(u)} f_v$ 就是 $\sum_i k^{\underline{i}}b_i(\sum_{v\in subtree(u)}f_v)$. 前面那部分不变, 问题就是 $\sum_i \sum_v b_ix^i(\sum_v f_v)$, 设 $S_u=\sum_{v\in subtree(u)} f_v, A_v=1+siz_v\cdot x, B_v=S_v(1+(n-siz_u)x)$, 就是选一个 $B$, 其他都选 $A$ 的多项式的和, 可以用消失之物的那种分治去分治FFT算.
总复杂度 $n\log^2 n$
CF724E Goods Transportation
小明升任了 CF 国的大总管, 他管辖的 $n$ 个城市, 编号为 $1. . n$. 每个城市生产了 $p_i$ 个货物, 限制最多可以卖掉 $s_i$ 个货物. 对于每两个城市 $i, j$, 如果 $i < j$, 则可以最多从 $i$ 运送 $c$ 个货物到 $j$. 注意不能反向运送, 却可以在多个城市之间送来送去. 现在小明想知道, 经过运输后, 最多能卖掉多少个货物.
$n\le 10^4$
考虑一个简单最大流: $S\stackrel{p_i}{\longrightarrow} i, i\stackrel{c}{\longrightarrow} j, i\stackrel{s_i}{\longrightarrow} T$ 即可, 但即使前后缀优化建图看起来也过不了.
考虑转化成最小割设计dp, $f_{i, j}$ 表示前 $i$ 个点其中有 $j$ 个到 $s$ 有边, 那么对于新的 $i$ 要么割 $s\to i, a\to i(a<i)$, 要么割 $i\to t$, 对应转移即可. 复杂度 $n^2$.
两个ppt过一遍了! 联赛完有空再去看第三个! 接下来该练练码力!
杂题选讲2
CF1407E Egor in the Republic of Dagestan
给定一张有向图 $Graph(n, m)$, 边, 点有黑白两色, 边的颜色给定, 每个点只能走和它颜色相同的边, 求把点染色后 $1\to n$ 的最短路最大值, 不连通视为 $inf$.
$n, m\le 5\times 10^5$
考虑每个点的选择只和它出边有关, 所以从后往前做, 直接bfs看每条边能不能堵死就可以了.
CF1370F2 The Hidden Pair (Hard Version)
交互题, 给定一棵树和未知点对 $(u, v)$, 每次可以询问一个点集, 得到其中使 $dis(u, w)+dis(v, w)$ 最小的 $w$ 和最小值, $11$ 次询问找到未知点对.
$n\le 1000$
考虑如果点集中有一个点在 $u, v$ 之间, 则 $w$ 是这个点, 最小值是 $dis(u, v)$, 所以要想办法让在 $u, v$ 之间的点尽可能少, 同时要想着利用我们得到的, 确定在 $u, v$ 之间的点 $x$.
根据这两个思想, 发现问与 $x$ 距离为 $\max dis(x, u), dis(x, v)$ 的点可以得到一个端点: 因为这个圆上的其他点必定不在路径上, 于是就得到一个端点, 然后去问与这个端点距离 $dis(u, v)$ 的点即可得到另一个端点.
于是问题是求 $\max dis(x, u), dis(x, v)$, 考虑二分, 发现很好判断: 最小值不是 $dis(u, v)$ 就说明当前答案大了, 于是就做完了.