置换群论学习

我们要解决的问题是, 给定一个对象集合 $A$ , 一个颜色集合 $B$ 和一组针对映射的变换 $G$ , 求有多少种映射(将对象集合映射到颜色集合)的方案是本质不同的, 这里两种映射本质不同指不能通过变换把一个变成另一个.

简单理解就是对对象染色, 如果可以通过翻转旋转之类的操作变化到的算一种, 求有多少种染色方案. 要求这个变换操作关于他们的复合构成一个群, 称为置换群, 变换称为置换.

符号约定:

$F(A, G)$ 表示对 $A$ 染色, 在 $G$ 的情况下的本质不同方案数
$G(c)$ 表示应用到 $C$ 上不改变的置换组成的集合
$C(f)$ 表示 $f$ 作用上去不改变的方案组成的集合
$S(c)$ 表示和 $c$ 本质相同的染色方案组成的集合
方案 $c$ 经过置换 $f$ 得到的东西为 $cf$ , 先进行 $f$ , 再进行 $g$ (就是复合 $f$ 和 $g$ )的置换为 $h=fg$

Burnside引理

引理0

$G(c)$ 是群

照着定义显然成立

引理1

$$
\sum \vert G(c) \vert =\sum \vert C(f) \vert
$$

显然成立, 因为两边都是满足 $f$ 对 $c$ 没用的有序对 $(f, c)$ 的个数

引理2

作用在方案 $c$ 上与 $f$ 效果一样的置换 $g$ 数量为 $G(c)$ .

$$
fc=gc\
f^{-1}gc=c\
h*c=c
$$

这里因为构成群, 可以保证 $f^{-1}$ 和 $f^{-1}*g$ 一定存在, 同时对于一个 $f$ 满足 $g$ 和 $h$ 一一对应, 所以成立

引理3

$$
\vert S(c) \vert =\frac { \vert G \vert }{ \vert G(c) \vert }, \vert G(c) \vert =\frac { \vert G \vert }{ \vert S(C) \vert }
$$

由引理2, 可知每个 $f$ 有 $\vert G(c)\vert$ 个和它作用到 $c$ 上效果相同, 那么它们就构成了一个大小为 $G(c)$ 的等价类, 由于一共有 $\dfrac{\vert G\vert}{\vert G(c)\vert }$ 个等价类, 不同等价类会把 $c$ 置换成不同的东西, 所以定理成立.

引理4

$$
\sum_c \frac {1}{S(c)}=F(A, G)
$$

原因是每一组等价的 $c$ 正好加成了1

Burnside引理

$$
F(A, G) = \frac{1}{ \vert G \vert } \sum_c \vert G(c) \vert =\frac{1}{ \vert G \vert } \sum_f \vert C(f) \vert
$$

第二个等号直接用引理1得到, 较为显然. 而第一个等号是组合定理4和定理3:

$$
F(A, G)=\sum_c \frac{1}{S(c)}=\frac {1}{ \vert G \vert }\sum_c \vert G(c) \vert
$$

于是命题得证.

应用时, 因为置换一般远比方案少, 所以第三种形式比第二种形式常用.

Polya定理 (声调飞了)

那如何快速计算 $C(f)$ 呢, 考虑我们可以把一个置换写成这个形式:

$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
3 & 1 & 2 & 5 & 4
\end{pmatrix}
$$

表示1变成3, 2变成1, 3变成2, 4变成5, 5变成4. 这里数字表示的是染色对象集合里的元素, 比如一个圈把它旋转一下, 对应的大概就是:

$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
2 & 3 & 4 & 5 & 1
\end{pmatrix}
$$

这个形式, 表示第1个的颜色变成了第2个的, 第2个的变成了第3个的. . . 第5个的变成了第1个的.

而这个东西又可以再分解成若干个循环, 比如第一个例子我们换一个说法:

$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
3 & 1 & 2 & 5 & 4
\end{pmatrix}
$$

表示1变成3, 3变成2, 2变成1, 4变成5, 5变成4

相当于拆成了若干个首尾相接的置换的复合, 即

$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
3 & 1 & 2 & 5 & 4
\end{pmatrix}
=
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
3 & 1 & 2 & 4 & 5
\end{pmatrix}
*
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\
1 & 2 & 3 & 5 & 4
\end{pmatrix}
$$

我们称拆出来的一个为一个循环, 因为它是首尾相接的一个环, 那么一个循环里如果有任意两个元素不一样, 被这个循环置换一下就不一样了, 所以对于 $C(f)$ 的每个染色, 都要求一个循环里的元素被染成了相同的颜色. 而不同的循环是互不影响的, 所以得到

$$
C(f)=m^{k(f)}
$$

其中 $m$ 表示颜色总数, $k(f)$ 表示 $f$ 可以拆成多少个循环, 这就是polya定理了, 完整形式可以是

$$
F(A, G)=\frac {1}{ \vert G \vert }\sum m^{k(f)}
$$

例题

P4980 [模板]Pólya 定理

$t$ 次询问计数用 $n$ 种颜色对一个长 $n$ 的项链染色的本质不同的方案数, 两个方案本质相同指可以通过旋转(注意不能翻转)从一个变成另一个.

$t \le 10^3, n\le 10^9$

对一种颜色的数量没有限制, 一个置换就是把它转几下满足群的定义, 可以Polya, 问题是怎么算 $k(f)$ , 即怎么算旋转 $i$ 步的置换能拆成几个循环.

考虑在旋转过程中, 每个位置开始的情况是一样的所以在一个循环中不会重复经过一个数, 拆出的每个循环的情况是一样的所以每个循环的长度相等. 由于一个位置回到原位走的路程是 $\mathrm{lcm}(n, i)$ , 也就是转了 $\frac{\mathrm{lcm}(n, i)}{i}$ 步后回到原来的位置, 也就是单个循环长度, 所以循环个数就是 $\dfrac{n}{\frac{\mathrm{lcm}(n, i)}{i}}=\gcd(n, i)$ , 于是就是要求

$$
\sum_f{n^{k(f)}}\
=\sum_i n^{\gcd(i, n)}\
=\sum_{d \vert n} n^d\sum_i^n [\gcd(i, n)=d]\
=\sum_{d \vert n} n^d\sum_i^{\frac{n}{d}} [\gcd(i, \frac{n}{d})=1]\
=\sum_{d \vert n} n^d\varphi(\frac{n}{d})
$$

因为 $n$ 很大很难预处理, 但直接暴力就能过. 因为 $10^9$ 次方以内只有 $10^3$ 量级的因子, 每个再平均 $\sqrt{\sqrt{n}}$ 的求, 界就很松.

P4727 [HNOI2009]图的同构计数

问 $n$ 个点组成的不同构的完全图的个数, 两个图同构指它们可以通过重编号顶点相同.

$n \le 60$

一个置换就是对顶点重编号, 一共有 $n!$ 个置换

考虑对一个置换如何算它的 $C(f)$ , 这里的困难在于置换是对顶点的, 但染色对象确是对边的, 需要先把对顶点的置换转化为对边的.

考虑一个顶点的重标号, 会形成若干循环, 考虑一个边要么连接两个循环, 要么在同一个循环里:

对于同一个循环里的边, 设循环长度为 $len$ , 发现这个点的置换关于边形成 $\dfrac{len}{2}$ 个循环, 如果不明白可以看这张图:

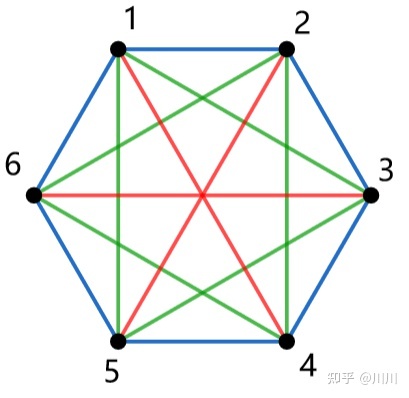
其中每个颜色代表了一个循环, 根据一条边跨越了几个顶点分类.
对于不在同一个循环里的边, 若两个循环大小分别为 $a, b$ , 则一共有 $ab$ 条这样的边, 此时相当于每个时刻有两个环一起转一步, 我们考虑一条边什么时候会回到原位, 发现小学数学可知它 $\mathrm{lcm}(a, b)$ 步后会回去, 所以一个边的循环大小为 $\mathrm{lcm}(a, b)$ , 所以个数就是 $\gcd(a, b)$ 个.

于是, 对于一个点的置换, 设它拆成大小为 $a_1$ , $a_2$ . . . $a_k$ 的循环, 那么它对于边的循环个数为

$$
\sum_{i=1}^k \dfrac{a_i}{2}+\sum_{i=1}^k\sum_{j=1}^{i-1}\gcd(a_i, a_j)

但现在由于我们要遍历 $n!$ 个置换, 仍然无法通过, 发现其实一个置换我们只关心每个循环的大小, 每个循环由哪些点构成是不重要的, 所以我们可以直接枚举所有循环大小的情况, 即枚举不同的升序序列 $A=a_1, a_2. . . a_k$ , 并计算有多少个置换会拆成这样的序列.

首先任意排列有 $n!$ 种, 再除掉每组内的相对顺序 $a_i!$ , 每组里是个圆排列乘上 $\dfrac{a_i! }{a_i}$ , 最后因为大小相同的组是不计顺序的, 设 $v$ 出现了 $c_v$ 次我们要再除掉 $\prod_v c_v!$ , 所以次数为

$$
\frac{n! }{a_i\prod_v (c_v! )}
$$

所以最后方案数为

$$
\frac{1}{n! }\sum_A \frac{n! }{a_i\prod_v (c_v! )} \times 2^k\
k={\sum_{i=1}^k \dfrac{a_i}{2}+\sum_{i=1}^k\sum_{j=1}^{i-1}\gcd(a_i, a_j)}
$$

拿这个算就好了. 我们枚举的这个东西其实是拆分数, 60的拆分数大约在1e6量级, 再乘上 $n^2$ 看起来过不了, 但其实大多数拆分项数较少, 所以跑的飞快.

CF1630E Expected Components

给一个长 $n$ 的序列 $A$ , 求随机一个 $A$ 的本质不同排列其权值的期望

定义两个序列本质不同当且仅当不能通过旋转得到

定义一个序列的权值, 为若相邻两数相同则连边, 最后形成的连通块数, 注意 $a_1$ 和 $a_n$ 属于相连的.

$n \le 10^6$

首先这个连通块数等于 $a_i\ne a_{(i\bmod n) +1}$ 的数量, 但要记得特判全相等的情况.

这个本质不同让人很想 burnside 或 polya , 但 $A$ 中可能会有相同的数导致不能用 $m^{k(f)}$ 的形式, 考虑burnside.

此外, 容易发现答案与 $A$ 中数的出现次数有关, 于数的大小无关, 所以用 $cnt_v$ 表示 $v$ 的出现次数, 颜色个数为 $k$ .

分成两步, 求本质不同的排列数和求答案.

求本质不同方案数

burnside后我们要计算一个置换的作用上去不变的数量(不动点), 考虑现在若是转 $i$ 步, 根据上面 polya模板那题的结论, 会有 $\gcd(n, i)$ 个长为 $\frac {n}{\gcd(n, i)}$ 的循环, 设循环长度为 $d$ , 考虑如果一个循环不是同一个颜色则一定不可能不变, 所以每个循环必然是同一个颜色, 也就是 $d \vert \gcd(cnt_1, cnt_2. . . cnt_k)$ , 令所有 $cnt$ 的 $\gcd$ 为 $g$ .

而当可以满足每个循环颜色均相同时, 我们可以直接用可重排列来做, 因为循环与循环是区分的, 但同种颜色的每个数是不区分的, 同种循环之间也是不区分的, 所以不动点个数为

$$
\dfrac{\dfrac{n}{d}! }{\prod_i \dfrac{cnt_i}{d}! }
$$

算一个置换的不动点个数是 $O(k)$ 的. 由于 $\sum_i cnt_i = n$ , 所以 $g=\gcd(cnt_1, cnt_2. . . cnt_k)\le \dfrac {n}{k}$ , 所以我们只算 $d \vert g$ 的不动点, 那么复杂度就是 $O(k\times \dfrac{n}{k})=O(n)$ .

为了方便, 这里记循环长度为 $d$ 的不动点数量为 $fixpoint_d$

求答案(权值和)

接下来要求答案, 考虑使用带权burnside, 形式为:

$$
\begin{aligned}
sum = \dfrac{1}{ \vert G \vert }\sum_f w(C(f))\
w(C(f))=\sum_{c\in C(f)} w(c)
\end{aligned}
$$

要算每个 $f$ 的 $w(C(f))$ , 这种问题常常要把贡献拆开, 发现一个特点是, 在上一步我们计算不动点个数时把所有 $cnt$ 和 $n$ 都除以 $d$ , 本质相当于我们去算一个长为 $\dfrac {n}{d}$ 的数组的可重排列, 而最关键的是若原序列两个位置是相邻的, 它们所在的循环一定也是相邻的, 所以我们考虑如何算在这个数组上两个相邻元素的贡献.

一个相邻而不想等的贡献应为确定这个之后其他的排布方案乘上它自己的贡献, 即

$$
\begin{aligned}
&\frac{(n-2)! }{\prod_{i=2} cnt_i! }\times d\times \dfrac{n}{d}\
=&fixpoint_d\times \frac{1}{n(n-1)}\times cnt_1\times cnt_2\times d\times \dfrac{n}{d}
\end{aligned}
$$

最后乘上 $d\times \dfrac{n}{d}$ , $d$ 是因为新数组每相邻两个之间的贡献为 $d$ , $\dfrac{n}{d}$ 是因为新数组上有这么多个位置, 我们当前算的两个东西可以在里面随便挑一个相邻.

所以总和就是

$$
fixpoint_d \times \frac{1}{n(n-1)}\times sum\ of\ cnt_i\times cnt_j\ s. t. (i\ne j)\times d\times \frac{n}{d}
$$

然后算就好了, 复杂度 $n \log n$ , $\log$ 来自 $\gcd$ .