网络流选做

建图套路深

费用流边的描述用 $u \stackrel{f, c}{\longrightarrow} v$ , $f, c$ 分别是流量和费用.

题目

P5458 水晶 [网络流] [最小割]

对于水晶, 染色时能量源染成一种, 能量源周围六个点间隔着染两种, 发现若共振则一定三种颜色都包含且相邻, 同色格子互不影响

于是可以每个能量源拆三个点, 分别表示三种颜色删去哪一种, 串联起来跑最小割, 表示从这三种任意删一个

P2774 方格取数问题 [网络流] [最小割]

黑白染色, 做成二分图, 两种颜色各一边.

对于一个格子, 向源点或汇点连自己点权的边(取决于自己在哪一边), 向周围四个格子连容量inf的边, 跑最小割即可

[思考] : 限制明显而许可(可以这么做)不明显时最小割

P5038 奇怪的游戏 [网络流] [思维]

看到相邻的两个格子想到黑白染色后一定一黑一白

于是黑白染色, 统计黑, 白色格子个数和权值和, 记为 $cnt_b, cnt_w, sum_b, sum_w$ , $sum_b-sum_w$ 始终不变设最后所有数都变成x, 接下来分两种情况

如果黑白格子数量相同, 因为权值差不变, 如果一开始不相等可以直接特判掉, 所以 $sum_u=sum_v$ 发现两者相同的情况下, 棋盘的长或宽一定有一个是偶数, 所以可以用相邻格子平铺使x+1, 所以答案具有单调性, 可二分
如果不同, 则 $sum_b - sum_w = x\times(cnt_b - cnt_w)$ , 解释一下就是因为操作时两者差始终不变, 所以一开始的差等于结束的差, 解出x后也要判断一下

于是要考虑如何判断是否可行, 对每个格子算出还剩几次操作到 x, 然后染色后分成两边, 向源点汇点连自己剩余次数的边, 中间连inf, 判断最大流是否流满

P4553 80人环游世界 [网络流]

每个点拆入点出点, 之间连上下界都是经过次数的边, 费用为0, 然后点之间正常连, 跑费用流

P4043 支线剧情 [网络流]

上下界网络流板子, 下界为1, 上界inf

上下界网络流方式是, 每个边流量设成上界-下界, 然后对于每个点出边下界和和入边下节和之差进行补流, 最后还要记得给汇点到源点连一条流量inf的边

P1646 happiness [网络流] [最小割]

建两个点表示文理, 从文科连到同学连到理科, 对于两个人同时选一科的情况建一个点, 一边连文理, 流量为共同选这个科目的开心程度, 另一边连这两个人, 边权为inf, 最后跑最小割

CF277E Binary Tree on Plane [网络流]

拆点成u1, u2, 每个点u1向所有可能的儿子的u2连容量1, 费用为距离, 源点像所有u1连容量2, 所有u2向汇点连容量1, 费用为0, 跑最小费用流.

CF103E Buying Sets [网络流] [最小割]

有一个大小为 $n$ 的全集, 每个元素是一个数 $a_i$ , 有 $n$ 个子集. 题目保证任意 $k$ 个子集的并的大小 $\ge k$ .
每个子集有一个可正可负的权值, 你需要选出一些子集使得这些子集并的大小等于子集个数, 且所选子集的权值和最小. 可以为空集.
$n\le 300$ , $a_i\in [1, n]$

好厉害的网络流!

当你试着搞费用流模型建图, 你会发现边需要是阶跃函数, 就寄, 此时如果确实是网络流题多半是最小割题了. 但这个题还是见过的极为巧妙的最小割问题.

建图是源点向所有表示集合的点连 $inf-a_i$ , 集合向元素连 $inf$ 的边, 元素向汇点连 $inf$ 的边. 并且选择一个集合是保留它的边, 选择一个数字是断掉它的边, 最后局面就是选了的集合里所有数字被断掉.

那么考虑这么做能保证集合数量等于元素数量, 由于每条边都加 $inf$ , 我们会断尽量少的边, 再考虑可以直接断所有右边的数字, 所以我们一定只断 $n$ 条边, 于是选的数字的个数和不选的集合的个数总和是 $n$ , 那么选的数字的个数就是选的集合的个数了.

十分巧妙啊!

要点主要是, 想到最小割后要想到全集是一种方案, 且不选集合的个数和选的数字的个数一定, 那么你很容易想到都加 $inf$ 这一步, 然后再针对构造.

CF132E Bits of merry old England [时间轴建图] [最大流] [网络流]

一个有 $n$ 个数组成的序列 $a$ , 你有 $m$ 个寄存器, 每次你可以给一个寄存器赋值为 $x$ , 代价为 $\mathrm{popcount}{x}$ , 或者输出一个寄存器, 代价为 $0$ , 求最小的代价按顺序输出这个序列. 输出方案.
$n\le 250, m\le 26$

极为厉害的网络流.

只能对时间建图. 并且有个贡献消除.

变量可以一直保留这件事十分毒瘤, 考虑变量不能保留, 但如果一个变量从上一次保留到这里, 我们在后面减去这一次赋值的代价.

看这个建图:

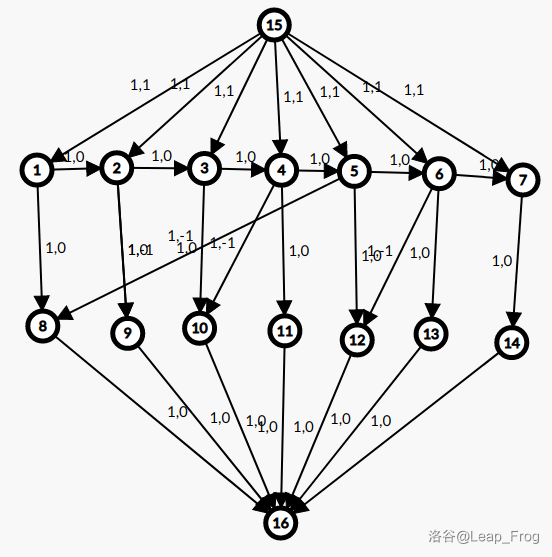
buildgraph

对每个 $a_i$ 建立两个点 $u_i, u_i’$ .
- $u_i\stackrel{1, 0}{\longrightarrow}u_i’$ 表示输出 $a_i$ 这一变量
- $s\stackrel{1, \mathrm{popcount}(a_i)}{\longrightarrow} u_i$ 表示这一时刻你进行赋值 $1$ 个变量, 花费 $1$ 的代价.
- $u_i’\stackrel{1, 0}{\longrightarrow} t$ 表示你输出 $1$ 个变量.
对每个 $u_i\stackrel{m-1, 0}{\longrightarrow} u_{i+1}$ , 表示上一时刻赋值的变量中有 $m-1$ 个.
对每个 $u_i$ , 设 $j$ 是最大的满足 $a_j=a_i$ , 连边 $a_i\stackrel{1, -\mathrm{popcount}(a_i)}{\longrightarrow}a_j$ . 表示上一次在 $j$ 处没有流 $u_j\to u_j’$ , 而是顺着 $u_i\to u_{i+1}$ 的边一直流到 $u_j$ , 再从这里回去流 $u_j’\to t$ , 就相当于把 $j$ 时刻的一个变量一直保留到现在.

然后就做完了, 输出方案的时候哪些 $u_i\to u_j’$ 的边被流了就能知道是不是被保留了.

太神仙了网络流.

CF164C Machine Programming [时间轴建图] [最大流] [费用流] [网络流]

直线上 $n$ 线段 $[l_i, r_i]$ , 每个线段有价值 $c_i$ , 你要选择若干条线段, 可以重叠, 但一点处最多有 $k$ 个区间重叠
$n\le 1000, k\le 50$

居然没见过这类网络流. . . 见识少了. 但一旦提示网络流, 想到时间轴建图还挺简单的. (可能是受上面那题影响? )

时间轴建图, 那么一个点最多有 $k$ 个重叠可以看作最多有 $k$ 个区间左右端点分属区间两侧, 那么直接每个时刻建一个点, 用 $(k, 0)$ 的边串起来, 对每个区间 $r_i\stackrel{1, c_i}{\longrightarrow}l_i$ , 跑最大费用任意流, 但因为权值全是正的所以跑最大流就行了.

P3980 NOI2008 志愿者招募 [网络流] [时间轴建图]

其实很早以前就做过了, 不过qyc今天在看这个题学网络流.

给定长 $n$ 的数轴和序列 $a$ , 有 $m$ 种区间 $[l_i, r_i]$ , 费用是 $c_i$ , 求最小代价使得位置 $i$ 至少被 $a_i$ 个区间覆盖.

$n\le 1000, m\le 10^4$

考虑时间轴建图, 每个区间从 $r_i\stackrel{1, c_i}{\longrightarrow} l_i$ , 每个点向下一个点连 $(inf, 0)$ , 每个点拆成两个, 内部连 $(a_i, 0)$ , 就做完了.

qyc: “这种建图本质上是用一个环表示一个区间“

[ABC193F] Zebraness

给你一个 $n\times n$ 的黑白矩阵, 格子 $(i, j)$ 可能是白的(W), 黑的(W), 不确定(? ). 现在让你确定每个不确定格子的黑白, 使得两边颜色不一样的边数最大, 输出这个最大值. (这里的边指的是每个格子的边)
$n\le 100$

小清新网络流, 来自dwt的vp.

容易想到最小割建图.

然后你只需要把相邻各自颜色反向就可以把很容易做的相同限制(若 $u\in S$, 则 $v\in S$)变成相反限制(若 $u\in S$ 则 $v\in T$)

[ABC326G] Unlock Achievement

x> 有 $n$ 个技能, $m$ 个成就. 每个技能有一个等级, 初始均为 $1$.

你可以用 $c_i$ 块钱令技能 $i$ 提升一个等级, 该操作没有次数限制.

第 $i$ 个成就达成的条件是对于 $\forall j\in [1, n], level_j \ge L_{i, j}$, 其中 $level_j$ 表示第 $j$ 个技能的等级. 达成成就 $i$ 后, 你会获得 $a_i$ 元的奖励. 注意这里奖励与成本是分开的, 也就是说你不能用奖励的钱去提升等级.

请最大化获得的奖励与所需成本之差, 并输出该值.

$n, m\le 50, , 1\le L_{i, j}\le 5, , 1\le a_i, c_i\le 10^6$.

退火!

这是个网络流题, 费用流很难处理不连续的收益, 考虑最小割, 对每个第 $i$ 个技能为 $j$ 级建点, 把 $6$ 个点串成一串, $t$ 连到 $6$ 级 $inf$, $j$ 级和 $j+1$ 级连 $jc_i$, 用割掉从下往上第 $i$ 条边表示选 $i+1$, 然后每个奖励会和 $i$ 的 $L_i-1$ 级连.

qyc讲课

建图

CTT22001177 无限之环

提示网络流题后, 容易想到相邻两个格子接头染色,

于是每个格子建表示向上下左右四个方向接头的四个点, 然后逐个分析出每个管子的边权即可.

CF1404E Bricks

注意到, 分析每个格子的边, 一个格子的邻边不能同时在同一个矩形内, 若一条边两边有一个格子是白色那就不能选, 于是就在每个格子内建边, 选的是二分图最大独立集.

循环流

做法是, 先强制满流正边(相当于上下界网络流预先流下界), 然后超级源和超级汇向每个点连边平衡, 此部分流量用来抵去所有超额部分, 这部分一定要满流才有解. (就是上下界弱化版啊).

志愿者招募

have done

ARC137E

循环流, 一条边表示一个位置, 一条反向边表示一个区间(类似上一个志愿者招募), 然后对 $a_i$ 取min是十分简单的, 两条费用不同的边即可.

HNOI2013 切糕

对每个格子建一列点, 割掉第 $i$ 条边表示第 $i$ 个点, 然后黑白染色, 相邻两个格子, 在两列格子跨度为 $d$ 的连 $inf$ 的边, 每列点顶上连源底下连汇, 但此时问题是可能会在一条链上删好几条边, 于是你在每个边权都加 $inf$ 就可以避免这件事.

人员雇佣

先全选, 用最小割表示限制, 让 $S\to i$ 表示选, 割 $i\to T$ 表示不选, 然后在任意两个 $i->j$ 连边, 在这个基础上赋边权跑最小割即可.

要点应该是你让它至少选不选都先断一条.

THUPC22 I. 分组

考虑仍然 $S\to i, i\to T$, 在上个题的基础上, 对 $(i, j)$ 建一个点 $c$ 也向源汇连边, 并让 $i\stackrel{inf}{\longrightarrow} c$, 最后只要给一些 $c\to i$ 这种东西就行了.

特殊图

单位圆图最大团

平面上任意两个距离少于1连边, 求最大团. $n\le 100$

注意到最大团必然在最远点对画半径为 $1$ 的圆的交里, 连这两个点把交划分成两部分, 则左右两部分都是团, 因此两部分都是二分图. 因为最大团是补图的最大独立集, 于是网络流跑二分图最大独立集即可.

CCPC2021 WEIHAI L. SHAKE HANDS

注意到 $\forall i < j < k$, 若 $i, j$ 没换过, $j, k$ 没有换过, 那么 $i, k$ 也没有换过, 于是小于并且没换过是偏序, 按照这个发现这个图的补图是可比图, 于是原图最大团补图最大独立集就是补图最长反链就是最小链覆盖.

剩下部分被qyc割了.

模拟费用流

费用流关于流量是凸的大家都知道

XX OPEN CUP GP OF KAZAN H. HONORABLE MENTION

先考虑全局, 用每条边表示一个 $a_i$, 费用为 $a_i$ 容量为 $1$, 每个点向源汇连边, 然后再加一些随便拆点就可以了. 于是要模拟费用流, 你可以建个线段树, $f_{i, j, 0/1, 0/1}$ 表示节点 $i$, 内部流量为 $j$, 左右端点连出去是否有流量, 因为费用流可以说明 $f$ 关于 $j$ 是凸的, 而你发现每次转移就是左右儿子做闵和.

那么区间问题的时候你要归并线段树上 $\log n$ 个区间, 因为我们只要求一个位置的值, 相当于你排序这 $log n$ 个区间的函数的差分取前 $k$ 大, 于是你二分那个第 $k$ 大的值, 然后在每个凸函数上求有多少个小于它的个数即可判定, 复杂度是 $3log$, ~~分散层叠成 $2log$ ~~

XX OPEN CUP GP OF SPB F. FESTIVE BAOBAB

首先费用流就是源连到根, 每个点连到汇, 因为源汇边不退流, 那么模拟费用流, 实际上这个图根本不带反悔的, 所以你干的就是每次找最小的.

ICPC SHENYANG L. FORGED IN THE BARRENS

考虑先把极差变成段内任意两个的差.

那么 $a_i$ 向源, 汇连边表示自己的贡献为正/负, 然后把所有 $a_i$ 双向穿一排, 但可能会有相交的, 于是拆两排解决掉这个问题.

然后你分析增广路发现, 每次要么是新加一个区间, 要么是在一个区间内再选一个最大一个最小, 用线段树维护区间最大最小值和区间内拆一个子区间的贡献, 再用set维护外部区间, 开一个堆维护全局最大值即可.

PA2013 RAPER

费用流怎么做是显然的. $S\to i, i\to i+1, i\to T$

那么你每次干的增广路是上去正着走或者上去反着走.

于是线段树维护, 注意到一个反向边容量有 $0$ 的区间不会再被减, 所以要维护每个区间当前的答案和所有点都减去区间最小值的答案, 后者维护左边极长有流量, 右边极长有流量的部分, 以及这个部分的最小值, 以及其他一些平凡物, 一共九个.

P1484 种树

考虑费用流建图, 假设用流量表示树, 那么可以用边表示坑, 用点表示坑之间的间隔, 就可以做到相邻两个只能选一个了.

于是就是每次取反一个区间并和左右两边的合并

增量网络

CF865D BUY LOW SELL HIGH

费用流和RAPER那个一样, 注意在一天买卖等于啥也没干所以不用管, 所以图建出来也是 $S\to i, i\to i+1, i\to T$.

然后分析增广路和负环, 决策仅有两种: 把这一支等到现在在卖, 或者把之前一次卖的不卖了现在卖. 一个堆即可.

网络流题目选做