分块选做
分块选做
省选分块显然也挂了, 感觉又能数据结构又练码力, 唯一的问题是不会做
P4108 HEOI2015 公约数数列 [分块] [分析性质]
[结论]:**一个序列前缀 gcd 是 log 段的函数!**因为每次gcd改变至少要除以2, 所以就 $\log n$ 段, 这个性质还挺优秀.
第二是发现序列长度为 $10^5$ , 但询问 $10^4$ , 放过了 $O(q\sqrt n \log n)$ 的做法
于是只需要考虑计算对于gcd的每一种取值是否可行即可, 如果线段树需要支持后缀异或一个数和查询一个区间是否存在某个数, 这是不可做的, 因为首先标记显然不能pushdown, 那么对于标记永久化, 可能会走到一个节点, 它一部分被打上了标记, 然后就G了
所以只能分块, 设块长为 $B$ , 对每个块维护块内 gcd 和 xor和, 再开一个哈希表存储当前块内前缀xor和为 $x$ 的最早的位置, 修改时暴力 $O(B)$ 重构当前块, 并对后面 $O(\frac{n}{b})$ 个块暴力, 询问则在外层从前到后遍历每一个块, 并在过程中记录当前块前缀 gcd 和 xor, 如果发现一个块前后 gcd不同, 则说明其 gcd 发生了改变, 在块内暴力扫一遍, 否则直接查维护的哈希表, 其实哈希表也可以map, 不影响复杂度. 由于gcd只会改变 $\log n$ 次, 所以这样做也只会暴力 $\log n$ 个块, 在B取 $\sqrt n$ 时总复杂度为 $O(n+q\sqrt n\log n)$
P4891 序列 [分块] [性质]
这个东西较难线段树, 然而据说貌似也可以, 但这里还是写分块做法, 把序列分成 $\sqrt n$ 块, 维护每一块 $\prod\limits_{i=1}^n \min(B_i, C_i)$ 的值和B的排序数组和B排序数组的前缀积数组
对于B的修改, 可以暴力重构所在块的答案, 排序数组和前缀积, 这里可以直接插入而不每次排序来砍掉一个 log, 复杂度 $\sqrt n$ .
对于A的修改, 由于C是A的前缀max, 所以一次修改相当于对一个后缀取 max, 若把位置 $i$ 修改为 $x$ , 可以二分最后一个满足 $C_i<x$ 的位置 $j$ , 相当于对区间 $[i, j]$ 赋值为x. 仍然暴力重构散块, 对于一个整块整体赋值为 $c$ , 则可以在 $B$ 排序后的数组中找到第一个满足 $B_i>c$ 的位置, 则答案就是两段拼起来, 直接二分的话会带个log, 发现这个c每次修改是单增的, 可以每一个块维护个指针, 一次对B的修改最多令一个块的指针移动一位, 应该就能砍掉一个 log
查询就暴力把每一块的答案乘起来, 最后总复杂度就是 $O(n\sqrt n)$
雅加达的摩天楼 [根号分治] [bfs] [暴力] [建图]
很妙的一个题, ~~虽然它是这个分块题单里不用分块和莫队的唯一的题. ~~
首先暴力, bfs状态为 $(pos, jump, time)$ 表示当前位置, 跳跃能力和已经用的次数, 则每次有三种转移:
- $(pos, jump) \to (pos+jump, pos, time+1) \ s. t. \ pos+jump<n$
- $(pos, jump) \to (pos-jump, pos, time+1) \ s. t. \ pos-jump\ge 0$
- $(pos, jump) \to (pos, p_i, time) \ s. t. \ b_i=pos$
比较显然, 最后一个多意思就是跳到一个楼上只后你换了一个 doge.
然后惊喜的发现这样暴力直接过了, 原因如下
- 首先每个(pos, jump)只可能对应一个最小的time, 也就是拿前两个判重
- 考虑进行根号分治, 对于一个 doge 的 $p_i$
- 若 $p_i\ge \sqrt n$ , 则它只能跳到 $\frac {\sqrt n}{p_i}\le \sqrt n$ 个位置, 一共只有 $m \times \frac {\sqrt n}{p_i}\le m \sqrt n$ 状态
- 若 $p_i< \sqrt n$ , 则一共n个位置, 每个位置一共 $\sqrt n$ 个可能的跳跃值, 所以一共只有 $n \sqrt n$ 个状态
然后这题实现的时候注意几个细节:
- 用 bitset 判重而不能用 map , unordered_map 也不行, 都会 TLE
- bitset空间玄学, 你可以开 $3\times 10^4$ 个大小为 $3\times 10^4$ 的 bitset, 但不能开一个大小为 $9*10^8$ 的
- BFS时边权有 0 有 1 , 所以要用双端队列 bfs, 注意标记访问过要在出队时, 不然可能会先有一个被扔到队尾的标记了访问使得后来要扔到队头的进不来
看到还有一种分层图的做法, 就是对于 $p_i>\sqrt n$ 可以直接暴力连边, 对于 $p_i\le \sqrt n$ 可以建立分层图, 每一层表示一个 doge, 层 $k$ 每个位置 $i$ 的点和 $i-p_k$ , $i+p_k$ 连边, 因为只对 $p_i\le \sqrt n$ 的建立, 所以层数只有 $\sqrt n$ , 也可通过.
王室联邦 [树分块] [分块]
树分块! 然而并不是我们分块常用的树分块, 更多给莫队用了
分块方法就是 dfs 每个点, 访问到一个点时, 维护一个集合表示还没有被分块的点, 然后依次遍历它的儿子, 把儿子中未被分块的点加进自己的集合, 如果大小超过 $B$ 就分一块, 首都为自己(而不是儿子), 最后把分块剩下的集合加上自己返回给父亲. 对于根节点, 剩下的部分塞进最后一个块里.
实现时可以用一个栈代替传递集合, 但要注意当前的栈底是进入这个节点时的栈顶, 而不是整个栈道栈底
这种分块保证了直径, 块内点个数和块数量, 但不能保证联通限制了较难应用在不是莫队的树分块上
P6177 Count on a tree II/[模板]树分块 [树分块] [分块] [bitset]
于是这是真正的树分块, 还是有挺多分块方法的, 这里只写几个最常用的
随机撒点法, 即完全随机的取 $B$ 个点, 每个点和它祖先中第一个关键点分为一块, 能满足
- 每个点到根的路径上期望经过 $n/B$ 个点能遇到一个关键点
- 一共 $B$ 个关键点
- 每一块点数期望 $n/B$
- 每一块直径期望 $n/B$
- 保证联通
对于这题, 可以预处理所有关键点两两之间的颜色构成的值域 bitset , 对于一个询问算出两个点的 lca, 于是分三类情况:
- 两个点到 lca 的路径上没有任何关键点, 则直接暴力
- 两个点到 lca 的路径上都有关键点, 则暴力从两个点向上跳到第一个关键点, 两个关键点之间的部分已经预处理好了
- 一个有一个无, 无的点直接暴力到 lca, 有的点先跳到第一个关键点, 然后再按关键点跳(每个关键点跳到它祖先中最深的关键点)到最后一个比 lca 深的关键点点, 这一段用预处理的, 最后再跳到lca
实现时第三种还是不要倍增, 因为并不能降低复杂度, 而且会在块长小的时候 WA , 原因如果倍增的数组不是处理的每个关键点的父关键点, 而是原本的父子关系, 最后并不能跳到最浅的比lca深的关键点
另外这题也可以仅处理关键点到它父关键点这段的答案, 但这样实现起来更麻烦, 因为一个询问要分成更多段处理, 然而预处理常数更小且空间小.
P5072 [Ynoi2015] 盼君勿忘 [莫队] [链表] [性质]
有人说不强制在线的YNOI常常是莫队
不强制在线和没有修改让人想到可以莫队. 首先考虑计算每个子序列的和必然是没有前途的, 所以考虑每个位置对这个区间的贡献, 由于要去重仍然不好办, 所以考虑每个值对区间的贡献, 只要计算它被多少子序列包含, 可容斥的计算又多少子序列不包含它, 发现若记 $v$ 出现次数为 $cnt_v$ , 区间长度为 $len$ , 则其被 $2^{len}-2^{len-cnt_v}$ 个区间包含, 贡献就是 $v \times (2^{len}-2^{len-cnt_v})$
这时我想到也许可以考虑加入一个值后每个答案都乘上了2, 再给它自己的答案除以2, 用数据结构维护, 然而由于每次询问模数不同导致这样做没有前途, 必须每次询问再计算答案.
[结论]:一个序列总长度 $n$ , 则值的出现次数的种类只有 $\sqrt n$ 量级, 推广对任意累计和为n的序列其不同元素数也是 $\sqrt n$ 量级, 原因是考虑 $1+2+3+. . . +\sqrt n = \dfrac {(1+\sqrt n)\sqrt n}{2}$
所以可以考虑维护每个出现次数对应的所有值的和, 由于乘法分配率则可以给它们整体呈上被包含数 $\sqrt n$ 计算答案, 于是接下来只要考虑在插入删除时如何 $O(1)$ 维护, 我们要有一个数据结构, 支持 $O(1)$ 把一个元素的值的一部分挪到相邻元素(就是挪到代表次数多1或少1的项中), 同时能 $O(\sqrt n)$ 的遍历所有有值的元素.
后一个条件让我们想起链表, 于是维护一个双向链表, 每一项存储 $cnt$ 和 $val$ 表示代表队出现次数和出现次数为 $cnt$ 的所有值的和, 但这样插入删除元素也是 $O(\sqrt n)$ 的. 于是发现可以开一个数组辅助记录每个出现次数对应的链表位置, 因为如果我们发现一个出现次数之前没出现并需要插入一个代表新的出现次数的元素时, 它左边或右边的节点一定存在, 使得我们可以 $O(1)$ 得到其前后元素, 那就可以 $O(1)$ 插入和维护这个辅助数组了.
这是不是最好写的Ynoi之一啊
P4117 [Ynoi2018] 五彩斑斓的世界 [分块] [大分块] [并查集] [链表] [性质]
~~64MB? problemprovidercreep! 无处存储! ~~
学到了一个卡空间技巧, 对于这种两个区间答案是独立的且可快速合并的时可以通过分块卡空间, 即每次只处理这一小块的答案最后合并起来, 用了一个 $O(\sqrt n)$ 的代价把空间缩小到 $\dfrac {1}{\sqrt n}$
于是接下来问题变成如何 $O(n)$ 求一个区间的答案, 由于这题值域也是1e5, 可以在这个方向思考一下, 这个做法是定义一个块的势能为这个块的最大值, 考虑如何处理操作, 发现如果我们维护一个全局(这一块的全局)加标记, 记块内最大值为 $v$ , 就有两种处理方式
- 给所有多于x的数减去x, 修改量为 $v-x$
- 全局减x, 并给所有少于x的数增加x, 修改量为 $x$
由于定义了势能, 所以要把操作量和势能挂钩, 发现
- 当 $v<x$ 时这块不用管
- 当 $x<v<2x$ 时, 用方案1会使 $v<x$ , 可以把势能减小最少 $v-x$ , 修改量也为 $v-x$
- 当 $v>2x$ 时, 用方案2会使 $v$ 减小x, 修改量也为 $x$
势能一开始是 $O(n)$ 的, 所以一块复杂度 $O(n)$ , 总复杂度 $O(n\sqrt n)$ 次修改
然后我们需要找到一个数据结构, 可以支持 $O(1)$ 的把一个值的元素改成另一个, 能 $O(\sqrt n)$ 查出一个时刻每个位置的值是啥, 发现可以对每个值开一个链表, 挂上它所有的位置, 然后当把一个值改成另一个只需把链表接起来, 查的话就是遍历所有的链表, 或者把链表换成vector启发式合并, 还有一种方法是用简化版并查集, 只要支持合并和遍历, 遍历因为一共 $\sqrt n$ 个元素, 合并每次都是合并两个根, 所以这个神奇并查集是 $O(1)$ 的
零散块查询和修改都是先还原每个点的值然后暴力重构或暴力判断相等
P4119 [Ynoi2018] 未来日记 [分块] [大分块] [并查集] [链表] [性质]
qyc瞬间就胡出了解法
既然是第一分块肯定要分块, 而且对于区间替换这个操作看起来很难线段树
对于查询, 两个可能都方案是二分和值域分块( $\sqrt n$ 分), 发现如果二分我们要么能 $O(1)$ 求出区间内小于一个数的个数, 要么就因为 $n\sqrt n\log n$ 被卡飞, 所以只能用 $\sqrt n$ 分, 即把值域分块, 因为反正都要顺着从下向上扫一遍块, 所以不需要维护小于一个块的个数, 而可以只维护区间内值在这个块的个数. 然后就是要能知道区间内在某一值域块内某个数出现的个数, 所以考虑在序列分块维护这两个信息, 做成两个前缀和, 即 $cnt_{i, j}$ 表示前 $i$ 块的数出现在值域 $j$ 块的数的个数, $cnt2_{i, j}$ 表示前 $i$ 块的数等于 $j$ 的个数, 散块可以套路的暴力, 这里可以先只暴力外层块的数, 再暴力某一块内的数(仅当这个数在这一块内才加进去).
对于修改把 $x$ 改成 $y$ , 分情况讨论
- $x$ 在区间中未出现或 $x=y$ : 跳过
- $y$ 在区间中未出现: 发现对于一次修改, 我们修改的是 $l$ 到 $r$ 的整块中 $j=x\ or\ j=y$ 的 $cnt2_{i, j}$ , $cnt_{i, j}$ 也同理, 即虽然单修改一个块影响 $\sqrt n$ 个后面的块, 但一个区间的所有块对后面的影响可以通过一个前缀和合并起来, 使得区间里的所有块对后面的影响可以用相同方式修改最多 $\sqrt n$ 个后面的块, 复杂度仍然是 $O(\sqrt n)$ , 此时这个修改相当于把一个数映射成另一个数, 可以直接开一个数组记录这个映射(即原数组中某个值的实际值和实际值对应的原数组值), 重构时先还原, 而整块修改时只要 $O(1)$ 的修改这个映射表即可.
- $x$ 和 $y$ 均在区间中出现: 此时修改相当于把 $x$ 合并到 $y$ 上, 考虑一个修改对于一个块内的数的种类数的种类数的影响, 完整包含时种类数不会增加, 部分包含则最多增加一, 由于一个块一开始种数最多有 $\sqrt n$ , 每次修改最多给种数增加2, 所以发现所有块的种类数减少次数的和(一次修改把两个数合成一个数)只有 $n+m$ 级别, 这使得我们可以不处理两个数合成一种数的情况而选择暴力重构, 因此只会执行 $O(n+m)$ 次这样的暴力重构.
然后在做这个200行大程序的过程中我查出了亿堆堆错误, 细节, 和可以更快的点, 这里总结一下:
值域分块和序列分块不要一起写, 便于调块长, 这个貌似真的会TLE一个点, 而且既然要调块长, 数组大小常量要两个分别是块长和块个数
寻址连续还是靠玄学两边都试试
分块的每块左端点和每个位置属于的块在Ynoi卡常题里还是存起来, 否则会TLE一个点
映射关系仔细想想, 主要是上面情况2中映射修改, 代码:
1
2
3
4
5//mapping[block][v]表示块block中数组中的v的实际值,reverse_mapping就是实际值对应的数组中的值
mapping[block][reverse_mapping[block][x]] = y;
reverse_mapping[block][y] = reverse_mapping[block][x];
reverse_mapping[block][x] = 0;
//**这里不能mapping[block][x] = 0,仔细想想发现它意义不对**使用 $\sqrt n$ 分时可以在求出答案在哪一值域块后再求散块的 $cnt_2$ , 只用处理在这一块内的就行了, 能快一些
最最最最最关键的我判断块内是否存在y的部分, 写的是
1
if(rever_mapping[y]==0) //二维数组!相当于判断空指针,始终为假全部暴力,关键是还能过一堆点让人以为是卡常了
P5397 [Ynoi2018] 天降之物 [分块] [大分块] [性质] [根号分治]
这次不是复杂度写假了, 而是真的常数爆炸
这里先写根号重构版, 以后如果有空可能会在那个序列分块加强的题做那种解法
一开始想的根号分治后给每个数维护 $O(1)$ 查询的kth和rank来支持前驱后继, 后来qyc说可以直接维护O(1)查询的前驱后继, 每次把一个点插进来修改的是一个区间, 然后才发现还有附属集合这种根号分治后套根号重构的妙法
首先和 SDOI2022 Day1T1 一样很容易想到根据出现次数进行根号分治. 维护每一个值的所有出现位置的有序数组, 和所有出现次数多的数对其他数的答案.
对于修改, 发现这个修改操作和第一分块的类似, 都具有一个势能均摊性质, 即对于把 $x$ 改成 $y$ , 两者都在序列中存在则每次种类数减一, 否则只要 $O(1)$ 修改映射, 因为一开始种类数是 $O(n)$ 的, 而次数较多的只有 $O(\sqrt n)$ , 所以对于两个次数多的的合并直接用 $O(n)$ 的暴力就 $n\sqrt n$ 了. 对于两个次数小的的如果合并后还是小, 就暴力归并一下, 否则仍然可以 $O(n)$ 重建, 原因是新晋次数多的数也是 $O(\sqrt n)$ 的, 这个理解就是如果两个后面被合并成大的了, 那你可以一开始就把它们看成一个大的, 由于这样后大的仍然不会多于 $O(\sqrt n)$ , 所以这样暴力归并也是对的, 最后就是一大一小的问题了, 这里使用了根号重构, 为每个块再开一个数组记录合并进来的不到 $\sqrt n$ 的数, 直到到了一起跑一个暴力归并, 这个的分析和两个小的合并成大的的相同. 由于要进行根号重构, 所以我们预处理的答案只包含整的部分, 零散部分不被包含.
修改过程中显然可以简单维护那个预处理的答案, 只要在合并两个数时, 遍历所有次数多的数, 更新答案为这两个数中较小的一个
对于查询只要暴力归并计算这两个零散块彼此间的贡献, 再查一查如果两个数是次数多的就再和预处理的答案取最小值即可
总复杂度是 $O(n\sqrt n)$ 的, 调出一份正确代码并不难, 但毒瘤把时限开到0. 5s , 内存开到256M 后就有些注意事项
- 每个值只用维护根号重构中的零散部分的有序数组, 整的只记录答案, 不然合并时还要归并整的有序数组常数爆炸
- 要用 vector 维护位置, 因为256M 开不下两个 $n \sqrt n$ 的数组, 而出现位置在每个数最大 $\sqrt n$ , 但总个数确是 $n$
- vector 调用
clear()后不会释放内存, 解决方案是紧接着调用vector. shrink_to_fit()或用网上流传的传统艺能开一个局部变量vector并和要清空的交换
祝卡常愉快
P6578 [Ynoi2019] 魔法少女网站 [Trick] [分块] [大分块] [性质]
上一个还可以是卡常愉快, 这个就直接毒瘤
这几个题似乎都是先考虑询问, 因为询问的形式多样, 但修改却形式少一些. “最大值小于等于 $x$ “就相当于这个区间的所有数都小于等于 $x$ , 可以用中位数或二分答案的套路把大于 $x$ 的设为0, 小于等于的设为1, 会得到若干个1的连续段, 发现长为 $len$ 的区间会贡献 $\frac{len\times(len-1)}{2}$ . 思考如何维护这个 $0\to 1$ 和 $1\to 0$ 的过程, 发现 $0 \to 1$ 的过程可以 $O(1)$ 的更新而 $1\to0$ 的过程不行(如何维护在后面序列分块)
为了区分, 把 $0\to 1$ 和 $1\to 0$ 的过程叫更新, 题目的修改叫修改.
在无修改的情况下, 容易想到如果把询问按x排序, 因为x单调增, 那么每个数符合要求后就一直符合, 只会被从 0 到 1 更新一次, 那现在加上修改, 一个比较厉害的做法(做题少第一次见)把所有被修改过的位置单独拿出来, 剩下的用上面的做法, 而对于这些被改过的位置, 每次询问遍历所有修改暴力更新, 算完询问再回滚撤销, 这样仍然复杂度爆炸, 但可以进行一个根号重构, 或者说时间分块, 即把每 $B$ 个操作作为一块, 块内这样处理, 每结束一块把所有修改作用上去重构.
因为一个块最多有 $B$ 个修改操作, 每个修改操作会被应用最多这个块的询问次(也是最大 $B$ ), 所以修改引起的更新次数就是 $\dfrac {n}{B} \times B^2=nB$ , 此外对于每一块, 会从小到大把每个没被修改过的位置更新一次, 一共 $\dfrac {n^2}{B}$ 次, 所以 $B=\sqrt n$ 时, 复杂度为 $n\sqrt n$ 最优.
所以就是要一个数据结构能 $O(\sqrt n)$ 求区间内的这个式子和, 并要支持 $O(1)$ 单点更新和撤销.
既然是Ynoi这个数据结构多半是分块, 可以序列分块, 每一块记录 $ans$ 表示块内答案(如果一个连续1区间伸出去了或延伸到区间端点整个连续段都不算, 不包含端点是因为包含端点的连续段会在查询时作为块间的算, 看后面), 以及块内的连续1区间的两个端点分别对应的另一个端点(即设数组 $begin_i$ 表示以 $i$ 结尾的全1区间的开头, $end_i$ 表示以 $i$ 开始的全1区间的结尾, 再记录区间全一前后缀长度, 此时一个修改有三种情况, 分别讨论着去修改, 注意前后缀长度单调增加, 均摊是 $O(1)$ , 注意只有整个区间都被包含时才算它的答案.
查询时对于散块可以暴力扫描, 对于整块如果全是1就是直接跳(判断前缀长度是否直接等于块长), 否则就给之前的长度加上最长前缀并计算这个区间的贡献, 然后更新下一个连续1区间的左端点为最长全1后缀的位置, 也记得加上这个区间的内部贡献.
至于撤销, 只要开个栈, 照着修改改了的信息记录一下就行了.
但按这个实现虽然复杂度时对的, 但还有不少细节:
可以用块分界线把全1段隔断, 即 $begin_i$ , $end_i$ 记录的是同一块内这个连续1区间的左右端点, ans记录的就成了不延伸到区间端点的贡献, 这样做就可以不维护区间前后缀长度, 中等优化
$begin$ 和 $end$ 可以用一个数组, 因为一个点要么是自己, 要么只能作为左端点或右端点, 较小优化
发现修改的时候常数仍然大, 要复杂的判断连续段是否连到了左右端点, 于是直接ans包含它们, 每次在查询的时候单独去掉前缀连续段和后缀连续段的贡献, 这一步有较大的常数优化.
栈要手写, 较大优化
每次完成一个时间块的处理后就不用撤销更新了, 直接
memset更新会更快, 较大优化预处理数组记录某长度的贡献
从小到大加入每一个数时不要用
sort, 虽然不影响复杂度, 但必须用桶排, 写vector或模拟邻接表反复调块长, 中等到较大优化
对于同一个位置的修改操作生效的是询问时间前最后一个, 同时如果对这个位置的修改在询问时间后要把原数组的值更新上
快读快写,
register, 开变量缓存等基本操作
于是再经过一小时写大约六七k代码再一小时调试正确性和加起来大概一天半的卡常就能过了, 这题时限简直# $%^$ %^%&^%& $%$
卡常卡常, 代码越卡越长
P4690 [Ynoi2016] 镜中的昆虫 [分块] [根号重构] [思维]
大分块做的太折磨了, 换几个不是大分块的做做. 可为什么这个我也写了250行啊
首先区间数颜色令人想起HH的项链, 考虑用同样的转化, 对于每个位置 $i$ 记录 $a_i$ 上一次出现位置 $pre_i$ , (同时为了方便下一次出现位置写作 $next_i$ ), 则区间查询 $[l, r]$ 中有多少 $i\in [l, r]\ s. t. \ pre[i]<l$ , 变成了个二维数点
那么下一步考虑修改, 对于单点修改发现修改一个点 $i$ 只会影响 $i$ 和 $next_i$ 的 $pre$ , 为了快速找到新的 $pre_i$ , $next_i$ 和 $pre_{next_i}$ , 对于每个颜色开一个 set 记录出现位置, 于是就成了一个带修二维数点.
而对于区间赋值, 体现出了这个题神仙的地方, 虽然单点赋值变成了区间赋值,但 $pre$ 的改变仍是 $O(n+m)$ 的!
考虑对于每个值相等的区间, 发现除了左端点之外的所有点 $i$ 满足 $pre_i=i-1$ , 此时若整个区间被改成另一个, 那么要更新的 $pre$ 就只有自己的左端点和下一块的左端点, 所以对于一次修改, 要更新的 $pre$ 就只有中间每个值域连续段的第一个和以每个值域连续段的 $next$ 的 $pre$ .
定义势能为当前总区间个数, 则每次的 $pre$ 变化量对应了势能的减少数, 同时一个修改最多增加3个势能(产生3个新的值域区间), 一开始势能为 $n$ , 所以**总复杂度 $n+3m$ **
于是就可以转化成单点修改了. 为了快速找到 $pre$ 的变化位置, 用一个 set 维护所有区间, 再用一堆 set 维护每个颜色的值域区间(后面这个就是把单点修改的 set 中的元素变成区间, 这两个 set 相当于把区间看成点. ) 就能 $O(\log n)$ 的找到一个区间的前驱后继, $O(cnt \log n)$ 的遍历连着的 $cnt$ 个区间了.
然后考虑如何处理单点修改的动态二维数点, 方案很多:
- 无脑树套树拍上去, 发现64MB内存炸飞了
- cdq分治大法好, 可惜我不会
- KDT玄学
- Ynoi怎能没有分块
于是写分块
最简单的想法是直接二维数点的分块, 先序列分块, 散块暴力, 整块要支持快速查块内小于一个数的个数和单点修改, 由于单点修改数 $O(n+m)$ 的, 而查询是 $O(n\sqrt n)$ 的, 值域分块维护就是 $O(\sqrt n)$
然后发现内存又炸了 (lxl点名卡的做法)
但有一种很巧妙的根号重构/时间分块做法可以 $O(n)$ 空间, 看另一篇题解写的有点简略, 我来说一说:
其实这个做法很像第十分块, 如果做过那个只要猛地听见”根号重构”, “时间分块”立马就会了.
具体的, 像第十分块一样, 当我们把询问按照 $l$ 排序, 元素只会变得更满足条件( $pre_i<l$ ), 所以可以从小到大加入每个符合条件的元素(就是对于每个 $pre_i<l$ , 给位置 $i$ 加1), 一共是 $O(n)$ , 然后对每个询问遍历这一块的所有修改, 判断一下是否要给答案加一, 这一步显然是 $O(q\times u)$ (即询问个数*修改个数)的, 而查询就是查询区间和.
套路的根号重构, 每 $\sqrt n$ 个跑一遍, 总复杂度 $O(n\sqrt n)$ . 另外为了保证复杂度, 区间求和单点加用 $O(1)$ 修改 $O(\sqrt n)$ 查询的分块平衡一下就行了.
这题代码量不小, 类似珂朵莉树的那块不少细节, 特判一下前后缀不存在的情况, 然后最重要的是注意STL的set在删除时迭代器会失效, 但又不是每次都会失效, 如果出现了开调试就对直接运行就WA之类的看看是不是用了失效的迭代器, 这种野指针解引用情况不会RE.
但好在时间良心, 我的实现一堆 STL 不卡常不快读就过了, 时间分块块长要稍大一点, 我是 $2\sqrt n$ .
其他地方的细节其他题解说的很清楚, 根号重构只要注意修改可能多次修改一个位置, 然后记得清空, 就是和第十分块一样的细节啦.
P6580 [Ynoi2019] 美好的每一天~ 不连续的存在 [大分块] [思维] [莫队] [分块]
传说中的势能均摊莫队, 代码先咕, 吐槽毒瘤的话等写了再放
如果直接回滚莫队+线段树合并, 由于线段树合并的复杂度是均摊的, 右指针复杂度 $O(n\log n)$ , 但左指针在块内反复撤销和合并是假的
由于在任意一个右端点的基础下左端点向左合并的代价必然不高于右端点是序列结尾的情况, 因为图是一颗树.
令位置 $l$ 的代价为当区间 $[l+1, n]$ 都被加入时的代价, 那么代价总和相当于从后往前扫一遍合并的代价, 是 $O(n\log n)$ 的.
此时把序列分块, 要求每一块大小都小于一个选定的阈值B(贪心的分即可), 再在这个上面跑莫队, 那么左端点移动就是 $O(Bm)$ .
而右指针的复杂度要求总块数, 如果一个块的大小小于 $\frac {B}{2}$ , 那么它下一个数一定要大于 $\frac {B}{2}$ , 所以这样的块个数是 $\frac {2n\log n}{B}$ 的, 于是块个数也正确了
最后拿这个分块方式跑回滚莫队, 复杂度应该是 $O(\frac {n^2\log^2 n}{B}+Bm)$ , 取 $B=\frac {n\log n}{\sqrt m}$
P5398 [Ynoi2018] GOSICK [大分块] [分块] [思维] [莫队]
十四分块是二次离线莫队这件事已经众所周知了. . . 而且它也确实是二次离线莫队最擅长的点对贡献模式
所以考虑如何莫队, 当一个数加入区间时, 贡献分成两部分, 它的倍数和因数, 这两块要分开考虑.
为了方便设 $f(l, r, x)$ 表示位置 $x$ 对区间 $[l, r]$ 的贡献, 同时记 $f=f_1+f_2$ , 分别是因数的贡献和倍数的贡献.
于是离线差分后贡献变成了两部分, 一部分是 $f(1, r, r)$ 或 $f(1, r-1, r)$ , 另一部分是f(1, l-1, r), 为了方便, 我们可以钦点自己不对自己产生贡献, 则可以把 $f(1, r, r)$ 当成 $f(1, r-1, r)$ 使用, 接下来单独讨论四种贡献的维护
- 预处理 $f_1(1, r, r-1)$ , 只需要扫一遍序列, 扫的过程维护一个桶记录所有数的出现次数, 到一个数时暴力枚举因数加入答案即可.
- 预处理 $f_2(1, r, r-1)$ , 仍然扫一遍序列, 扫的过程维护一个桶, 位置 $i$ 表示值 $i$ 是多少个数的因数, 就可以直接统计了
- 计算 $f_2(1, l-1, r)$ , 那么就是离线之后扫描过程中维护情况2. 的桶即可
- 计算 $f_1(1, l-1, r)$ , 此时这种倍数类的容易想到根号分治, 设阈值为 $B$ :
- 对于 $x\ge B$ , 暴力枚举倍数给答案加一
- 对于 $x<B$ , $x$ 的数量较少, 考虑如何对每个 $x$ $O(n)$ 计算答案, 那么对于离线后的一个询问 $q(p, l, r)$ 表示 $[l, r]$ 中的点对前缀 $p$ 的贡献和时, 每个 $[l, r]$ 中的点贡献相同, 那么只要知道 $x$ 在前缀 $[1, p]$ 中出现的次数和区间 $[l, r]$ 中 $x$ 的倍数个数就能做了, 于是记录 $x$ 的出现次数和倍数个数的前缀和.
这题的解法就这样了, 不过还有一些优化:
- 因数预处理存下来代替每次枚举
- 把对每个位置 $p$ 开 vector 记录 $q(p, l, r)$ 改为一起存进一个数组排序
- 快读快写
- 阈值开小! $\sqrt {5\times 10^5} \approxeq 700$ , 但我确实是开70左右能过.
P5309 [Ynoi2011]初始化 [分块] [思维]
容易想到根号分治, 修改时 $x>\sqrt n$ 可以直接暴力, 那么只要考虑剩下的部分.
此时x只有 $\sqrt n$ 种, 可以思考能不能对于一个询问单独计算每个 $x$ 的贡献加起来, 考虑对于相同的 $x$ , 如果把序列按 $x$ 为块长分块, 那么整块每一块被加的量相同. 而对于散块, 能贡献到一个块内区间的 $y$ 是一个连续区间, 所以可以以 $y$ 为下标开前缀和记录 $y\in[1, i]$ 的修改的 $z$ 之和, 散块就也解决了, 修改时暴力修改前缀和即可. 复杂度 $n\sqrt n$
还提过一个时间分块的想法, 但这个东西很难 $O(n)$ 重构, 就算重构也就是上面的做法所以寄了.
P6774 [NOI2020] 时代的眼泪
给定一个长 $n$ 排列, $m$ 次询问区间内值在某一区间的顺序对. $n\le 10^5, m\le 2\times 10^5$ .
我是十代的眼泪.
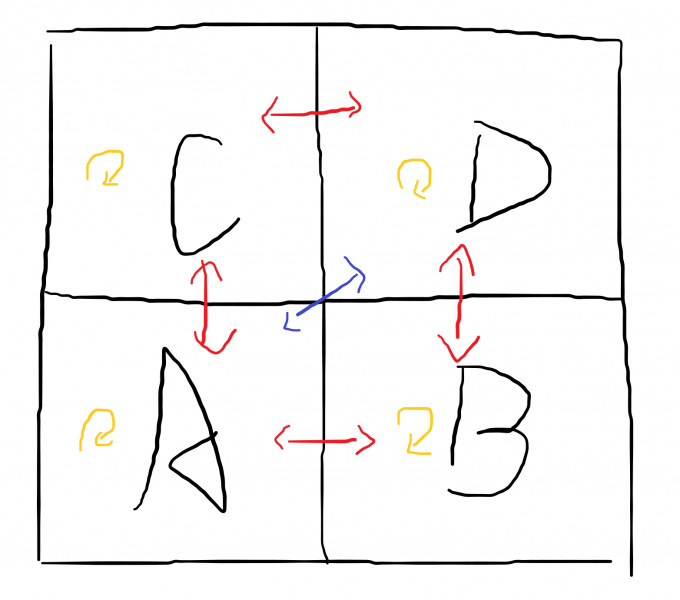
有
$$
\begin{aligned}
&ans(ABCD)\
=&ans(AB)+ans(CD)+ans(AC)+ans(BD)\
&-ans(A)−ans(B)−ans(C)−ans(D)+size(A)\times size(D)
\end{aligned}
$$
可以建立树套树, 内层节点对应二维平面上的一个矩形, 则可以分治求出每个矩形的 $ans, size$ .
那么接下来考虑如何处理询问, 每个询问在图上会拆成 $\log^2 n$ 个矩形, 那么贡献成了三部分:
每个小矩形内部的, 第一步已经预处理结束.
所有不同行且不同列的矩形, 这个的贡献相当于每个矩形左下方的矩形的 $size$ 的和. 可以一边遍历矩形一边求出.
同一行或同一列的, 行和列情况显然相同, 这仍然是一个二维矩形顺序对问题, 但好处是有一重限制为线段树的节点对应区间, 可以每个节点跑一遍二次离线莫队或分块. 对于复杂度, 考虑对每节点分别考虑, 若当前节点位于第 $k$ 层, 则复杂度为 $\dfrac{n}{2^k}\sqrt {q}$ , 这里 $q$ 是拆分到这个节点的询问, 然后我们在按层考虑, 每个询问会被拆成 $\log n$ 个节点, 但同一层只有两个, 所以每一层的询问总数为 $2m$ , 那么又因为发现当所有 $p$ 都相等的时候最大所以复杂度为 $n\sqrt{\dfrac{q}{2^k}}$ , 累加每一层的即为 $n\sqrt q \times \sum_i \dfrac{1}{\sqrt{2}^i}$ , 后面那个式子收敛于 $1+\sqrt 2$ 的位置为常数, 所以复杂度仍为 $n\sqrt q$ .
于是不卡空间的版本就做完了.
这个题启发了一种分治套分块的做法, 使得若分治后每一层的 $\sum a_i$ 和 $\sum b_i$ 一定, 则每个节点 $a_i\sqrt b_i$ 的复杂度套上分治后仍为 $n\sqrt n$ .
P8349 [SDOI/SXOI2022] 整数序列
给定整数序列 $a$ , $b$ , $q$ 次给定两个参数 $x$ , $y$ , 询问若构造序列 $c$ 满足 $c_i=[a_i=x]-[a_i=y]$ , 则找出区间 $[l, r]$ 最大化 $\sum_i=l^r b_i\times [c_i\ne 0]$ , 且满足 $\sum_i=l^r c_i=0$ .
$n\le 3\times 10^5, q\le 10^6, \vert b_i\vert \le 10^9, a_i\le n$
SDOI噩梦的开始, 送zrz退役的题
首先暴力做法和根号分治还都挺明显的, 暴力就是我们可以处理出所有数的位置, 每次归并两个数的位置, 然后搞一搞 $\sum b_i\times [c_i\ne 0]$ , $\sum c_i$ 的前缀和就可以了. 也容易想到对出现次数分治, 设阈值为 $B$ , 问题变为:
两数出现次数均小于 $B$ :
刚才的暴力, 复杂度 $O(qB)$ . 上
两数出现次数均超过 $B$
仍然是刚才的暴力, 但考场上错误的估计复杂度后直接寄飞.
设出现次数多于 $B$ 的出现次数分别为 $s_1, s_2. . . s_k$ , 复杂度显然是 $\sum_i \sum_j s_i+s_j \le nk \le \dfrac{n^2}{B}$ .
一大一小
这是最困难的部分了, 不过据说如果不会做这个在上一个基础上暴力判断小的次数为 $1$ 可以过题
但zrz一眼就秒了啊! 如果把小的插入到大的里面, 对于小的连续的长 $len$ 一段, 因为有 $c$ 的和为 $0$ 的限制, 所以其最多向左向右拓展 $len$ 个出现次数多的数就结束了, 于是只要暴力找出每个连续段向左向右的这些数, 再和小的本身的位置归并到一起, 然后用最初的暴力只跑这 $O(B)$ 个数即可.
简单实现
于是你就切完了这题, 然而细节还挺多的, 包括:
- 一大一小不能只向左右找 $len$ 个, 而要找 $len+1$ 个, 否则会出现忽略两个连续段中间的东西把两个连续段最左最右形成一个区间的情况.
- 搞连续段的时候不要重复添加中间的数, 主要是这一段的下标处理细节比较多.
- $\sum c_i$ 显然可以是负的, 谁把它直接放数组下标里了我不说.
[科技]-分散层叠
神仙科技, 因为常常用来优化多块二分所以放在这里了. 不过好像EI的论文里可以用这个实现 $O(\log n\alpha (n))$ 插入线段, $O(\log n)$ 询问单点最大值的科技啊.
分散层叠模板
给定 $k$ 个长均为 $n$ 的序列 $a$ , $q$ 次询问 $x$ 在每个序列的非严格后继(恰好大于等于的数).
要求 $O(nk)$ 预处理, $O(q\log n + qk)$ 查询.
对每个序列 $a_i$ 建立序列 $b_i$ , $next_i$ , $cur_i$ :
- $b_{i, j}$ 表示 $b_{i-1}$ 中所有偶数位置(即 $b_{i-1, 2k}$ )与 $a_i$ 归并起来的结果, 若 $i=1$ 则 $b_i=a_i$ .
- $cur_{i, j}$ 表示 $b_{i, j}$ 在 $a_i$ 中非严格后继的下标.
- $next_{i, j}$ 表示 $b_{i, j}$ 在 $b_{i-1}$ 中非严格后继的下标.
$b$ 通过每次归并就得到了, 而 $cur$ 和 $next$ 可以在归并过程中维护得到.
而查询的时候, 只要先从 $b_k$ 进行一次二分, 然后通过 $next$ 得到每一层的答案, 具体原理是, 若 $x$ 在 $b_i$ 的后继为 $b_{i, j}$ , 则其 $b_{i-1}$ 的实际后继下标与 $next_{i, j}$ 之差不超过1. 原因是考虑 $b_{i-1}$ 每隔一个就有一个在 $b_i$ 中.
实现起来会发现, 查询非严格后继和非严格前驱分别应在递增和递减序列里二分, 而严格的应分别在两者上直接减一.
你发现这个就很像从上一层渗透下来一部分和这一层融合到一起, 这样层层渗透下来, 所以被称为分散层叠.
简单拓展
如果不是每次渗透 $\dfrac{1}{2}$ 呢? 发现若每层渗透 $\dfrac{1}{p}$ , 则位置差少于 $p$ . 使得修改复杂度降低而查询复杂度增加.
同时, 我们这里渗透的结构是一层链( $i$ 渗透向 $i+1$ ), 实际上其可以是一个 $DAG$ , 或者更为有用的, 树.
但一考虑到修改这玩意就出问题了, 于是有了下面的技术让其支持修改.
线段树分散层叠
于是根据拓展部分的思考, 就有了这样的技术.
仍然是 $k$ 个序列的情况, 我们把渗透建一棵线段树, 由两个儿子各渗透 $\dfrac{1}{2}$ 得到父亲, 那么:
修改时, 我们从儿子出发, 会需要重新处理叶子到根一条链的信息. 若每次渗透 $\dfrac{1}{2}$ , 则单次渗透复杂度是 $O(n)$ , 修改复杂度为 $\log k$ . 然而平衡一下发现, 若每次渗透 $\dfrac{1}{p}, p>2$ , 则级数 $n+2n/p+4n/p^2+. . .$ 收敛, 复杂度就变成了线性.
接下来是查询, 查询单点随便做, 查询区间不可避免的带了区间长度的线性, 因为每次必须递归到叶子, 复杂度 $O(len+\log k)$ .
于是你发现这个东西用于多块二分刚刚好, 每个叶子对应一个块的话, 原来点名被卡 $O(\sqrt {n\log n})$ 就成了美妙的 $n\sqrt n+n\log n=n\sqrt n$
例题: 由乃打扑克
区间加, 区间 $kth$ .
发现区间加中间直接打标记不用动, 只要改散块, 把散块重新来一遍, 中间块打标记即可. 知道这个之后直接用裸的两层二分就实现了在线+空间线性+ $n\sqrt {n\log n}$ .