杂题(tricks)
做题笔记
几个杂题
P2150 寿司晚宴 [dp] [状压dp]
大于 $\sqrt n$ 的质因数最多只有一个, 最多出现一次, 相同大质因数一起处理, 背包合并
[trick] 大于 $\sqrt n$ 的质因数只有一个单独处理
P2048 超级钢琴 [greedy]
要求所有区间的前k大, 考虑处理 $k$ 次取最大, 开一个堆记录 $(l, rl, rr, t)$ 表示左端点为 $l$ , 右端点在 $rl$ 到 $rr$ 间时最优位置为 $t$ 的答案, 每次从堆中取出最优解, 把区间分裂成 $(l, rl, t-1)$ 和 $(l, t+1, r)$ 两个区间放回堆中
[trick] 把 $n^2$ 个点对贡献压缩成 $n$ 个 $p, l, r$ 表示一个点和区间 $l, r$ 中的点的贡献, $n^2$ 个可能贡献取前 $O(n)$ 个, 可能是先放能代表所有的, 一边拿一边把新的加入堆.
P3783 天才黑客 [ds] [virtual-tree] [最短路] [前缀和优化建图]
点边互换, 考虑对于一个点怎么把这些边连到一起.
考虑边之间的贡献是lcp, 那么可以转字典树上lca, 然后转字典树欧拉序最小值.
那么在这个序列上一个最小值会贡献前面一段后面一段, 用前后缀优化建图. 并且因为要对每个点单独跑一遍所以要用虚树.
最后可能会连出多余的边, 但是最短路保证了只会走最小值(重边自动取min), 所以是正确的.
[trick] 最短路最小值自动取min
P1763 埃及分数 [ida] [搜索]
居然是第一次写迭代加深
首先迭代加深主要是用在dfs搜索情况太多必然会挂, bfs每层情况太多存不下, 此时若能确定一个状态的后继状态的一个较小的范围那么就可以用.
如果我们决定每层分母从小到大, 也就是分数递减, 那么重点就是看每层的上下界, 设减去前面搜了的还剩 $\frac {a}{b}$ 要填, 当前分母为x, 后面还有 $rest$ 层:
当分母大到一定程度, 即使后面的都等于自己也到不了1时显然是不行的, 所以 $rest*\frac {1} {x} \ge \frac {a} {b}$
当分母小到一定程度, 即使后面都是0也超了更是不行的, 所以 $\frac {1} {x} \le {a} {b}$
最后, 这题似乎并没有靠谱做法, 至少在要求最大分母少于 $10^7$ 时讨论区里这组数据还杀遍程序无敌手:
1 | Input: |
P8350 [SDOI/SXOI2022] 进制转换
给定 $n, x, y, z$ 求 $\sum_{i=1}^n x^iy^{f(i)}z^{g(i)}$.
$f(i), g(i)$ 表示 $i$ 在二进制, 三进制下表示的数位和.
$n\le 10^{13}$
数据范围让你想到根号, 于是考虑折半.
因为看起来二进制结构更好, 所以考虑折三进制, 可以设数 $w=i+j\cdot 3^C_1$,
那么看起来 $x$ 和 $z$ 的贡献就是把项 $x^iz^{g(i)}$ 卷起来.
考虑二进制, 在依据刚才的 $C_1$ 划分后, 再按照二进制划分为 $C_2$ 使得 $2^{C_2}\ge 3^{C_1}$, 此时发现合并时低 $C_2$ 位是直接加, 问题是可能出一个进位, 于是只需卷两遍即可.
[trick] 折半, 卷积优化折半
P8330 [ZJOI2022] 众数
给定 $a_n$, 求区间 $[l, r]$ 使得区间内的众数出现次数和区间外的数的众数出现次数的和最大.
$n\le 5\times 10^5$, 3s
[trick] 出现次数相关, 根号分治.
大的部分, 枚举一个多于 $\sqrt n$ 的数, 处理出出现次数的前缀和, 再枚举另一个数作为内区间, 显然区间内这个数的出现次数要多于刚才的大数, 所以用SDOI2022 d1t1 trick让复杂度关于小数即可. 大数作为内区间同理.
小的部分, 考虑对于一个出现次数 $c$ 的颜色本质不同区间有 $c^2$ 个, 于是一共有 $n\sqrt n$ 个本质不同区间, 那么只要 $O(1)$ 算区间众数, 这显然不太可做, 性质是众数出现次数数根号级. 考虑扫描线, 对每个 $l$ 维护 $[l, r]$ 的答案, 那么当 $r$ 移动一个的时候, 遍历位置 $r$ 之前所有的出现位置 $x_1\ldots x_m$, 对每个 $x_j$, 从 $x_j$ 开始更新 $x_j, x_j-1\ldots$ 的答案, 如果不能更新直接结束, 这样因为更新总次数(也就是维护的答案总和)是 $n\sqrt n$ 量级, 所以复杂度是对的.
总复杂度 $n\sqrt n$.
[trick] 把答案作为势能(每次尝试更新答案)
CF1731F Function Sum
对于一个长度为 $n$ 的数列 $a$.
定义 $lsl(i)$ 表示 $i$ 左边的数中比 $a_i$ 小的数的个数, 即 $\sum\limits_{j = 1}^{i - 1}[a_j < a_i]$.
同样的定义 $grr(i)$ 表示 $i$ 右边的比 $a_i$ 大的数的个数, 即 $\sum\limits_{j = i + 1}^n[a_j > a_i]$.
我们称一个位置是好的当且仅当 $lsl(i) < grr(i)$.
我们再对于一个数列 $a$ 定义一个函数 $f(a)$ 为 $\sum\limits_{i = 1}^na_i[i\ \text{is good}]$.
现在给定两个整数 $n, k$, 请你求出对于所有长度为 $n$ 且 $1 \leq a_i \leq k$ 的数列 $a$ 的 $f(a)$ 的和是多少.
答案对 $\text{998244353}$ 取模.
$n\le 50, k\le 998244352$
容易发现每个位置对答案的贡献可以单独计算. 那么此时你试着算一个位置 $p$ 是好的的序列个数, 应该是
$$
\sum_a \sum_b \sum_v (v-1)^{a+n-p-b}(k-v)^{p-1-a+b} \cdot v
$$
这样的, 所以把 $v$ 当自变量就是多项式, 那么最后做一个前缀和次数增加一, 所以算前 $n+1$ 项+拉插
P7324 [WC2021] 表达式求值
定义二元操作符
<: 对于两个长度都为 $n$ 的数组 $A, B$(下标从 $1$ 到 $n$), $A$<$B$ 的结果也是一个长度为 $n$ 的数组, 记为 $C$. 则有 $C[i] = \min(A[i], B[i])$($1 \le i \le n$).定义二元操作符
>: 对于两个长度都为 $n$ 的数组 $A, B$(下标从 $1$ 到 $n$), $A$>$B$ 的结果也是一个长度为 $n$ 的数组, 记为 $C$. 则有 $C[i] = \max(A[i], B[i])$($1 \le i \le n$).现在有 $m$($1 \le m \le 10$)个长度均为 $n$ 的整数数组 $A_0, A_1, \ldots , A_{m-1}$. 给定一个待计算的表达式 $E$, 其满足 $E$ 中出现的每个操作数都是 $A_0, A_1, \ldots , A_{m-1}$ 其中之一, 且 $E$ 中只包含
<和>两种操作符(<和>的运算优先级相同), 因此该表达式的结果值也将是一个长度为 $n$ 的数组.特殊地, 表达式 $E$ 中还可能出现操作符
?, 它表示该运算符可能是<也可能是>. 因此若表达式中有 $t$ 个?, 则该表达式可生成 $2^t$ 个可求确定值的表达式, 从而可以得到 $2^t$ 个结果值, 你的任务就是求出这 $2^t$ 个结果值(每个结果都是一个数组)中所有的元素的和. 你只需要给出所有元素之和对 ${10}^9 + 7$ 取模后的值.$1 \le n \le 5 \times {10}^4$, $1 \le m \le 10$, $\vert S\vert \le 5 \times {10}^4$, $1 \le A_i[j] \le {10}^9$.
容易想到每一位独立, 考虑一位怎么做. 同时可以假设没有相同元素, 否则钦定大小关系. 另外建出表达式树也是显然的.
然后发现, 对于某一位能不能到最后, 只取决于有哪些数比他小, 与实际值和其他元素相对大小无关. 于是设 $f_{i, S, u, 0/1/2}$ 表示比 $a_i$ 小的节点集合是 $S$, 表达式树上节点 $u$ 的值比 $a_i$ 大/小/相等的方案数. 枚举 $i, S$, 转移是第四维上的max卷积. 复杂度是 $m2^m\vert S\vert$.
正解是考虑优化掉 $i$, 因为 $S$ 已经反映了 $i$ 的大小信息: 于是改成计算答案大于等于 $S$ 中的元素的答案, 这样就不依赖 $i$ 了, 状态可以改成 $f_{S, u, 0/1}$ $0/1$ 表示当前节点大于等于或小于(不在 $S$ 中或在 $S$ 中), 复杂度 $2^m\vert S\vert$
[trick] 只取一个序列中有效的大小关系在此题把 $n!$ 优化成 $2^n$. 将dp状态之间的关系利用好(如 $S$ 表示了 $i$ 的大小信息)
[AGC003E] Sequential operations on Sequence
一串数, 初始为 $1\sim n$, 现在给 $Q$ 个操作, 每次操作把数组长度变为 $q_i$(更短则截取前缀, 更长则不断重复原数组), $Q$ 次操作后 $1\sim n$ 每个数出现了多少次.
$1\le q_i \le 10^{18}$
首先变短操作之前的变长是没用的, 于是可以先把序列变成单调的. 显然我们不能维护整个数组, 于是想到设 $f_i(x)$ 表示第一个大于的 $q$ 进行完之后, 前 $x$ 个位置 $i$ 的出现次数, 那么有 $f_i(q_i)=(\lfloor \dfrac{q_i}{q_{i-1}} \rfloor)f_i(q_{i-1})+f_i(q_{i}\bmod q_{i-1})$, 于是考虑从后往前, 对每个 $f$ 维护其对最终结果的贡献系数. 右边部分因为每次膜比自己小的数, 最多递归log次, 直接做就行.
CF1394C Boboniu and String
什么烂题面, 容易发现实际上跟字符串是什么完全没关系, 就是只要B, N数量对, 然后发现每次操作你一定选增加的那个就行, 每次你可以让两者B, N的数量差同时加一或减一, 或者单独调一个. 那你就二分答案, 每个 $s$ 会给出一个对 $t$ 中B, N数量的限制, 判有无解即可.
CF1034C Region Separation
一棵 $n$ 个点的树, 每个点有权值. 你想砍树. 你可以砍任意次, 每次你选择一些边断开, 需要满足砍完后每个连通块的权值和是相等的. 求有多少种砍树方案. $n\le 10^6$
设权值总和为 $s$, 考虑假设砍到 $\dfrac{s}{d}$ 块, 每块大小为 $d$, 那么深度从大到小, 如果一个点大小不够就把它合并到父亲上, 如果正好是 $d$ 就分一段, 发现好像方案唯一? 实际上就是断所有子树大小为 $d$ 的倍数的点的父边, 最后要求这样的点有 $\dfrac{s}{d}$ 个. 于是先求出子树大小数组 $s$, 设 $f_d=\sum_i [d\vert s_i]$, 因为 $d$ 很大改为枚举 $\dfrac{s}{d}$ 即划分的块数 $k$, 则 $[\frac{s}{k}\vert s_u]$, 考虑一个 $s_u$ 对所有 $\dfrac{s}{gcd(s, s_u)}\vert k$ 有贡献, 那可以存进桶里枚举 $k$ 统计, 复杂度是调和级数. 然后要算 $g_k$ 为划分成 $k$ 块的方案数, 则 $g_k=f_k\times (\sum_{i\vert k} g_i+1)$.
最后复杂度是 $n\ln n$
[trick] 把树分成 $k$ 个连通块要求它们权值相等的方案数唯一, 条件为存在 $k$ 个子树大小为 $k$ 的倍数
CF1608F MEX counting
显然dp, 但mex显然不能记下来, 考虑把方案数拖到后面算上, dp设 $f_{i, j, k}$ 表示填完前 $i$ 个, 当前 $\mathrm{mex}(a_1\ldots a_n)=j$, 已经填过 $k$ 种不同的大于 $j$ 的值即可.
状态数显然是 $n^2k$, 瓶颈在填入 $j$(即更新 $\mathrm{mex}$ 时)需要枚举新的 $j$ 并计算贡献, 然后这个东西上个前缀和优化就转移 $O(1)$ 了.
P3352 [ZJOI2016] 线段树
容易想到拆成 $v=\sum_i [v>i]$, 此时相当于 $01$ 序列, 容易发现当前的 $0$ 的答案只和两边最近的 $1$ 相关, 于是设 $f_{i, l, r, v}$ 表示进行 $i$ 次操作, 当前考虑某个值是否 $>v$, 使得左边/右边最近的 $1$ 分别在 $l-1, r+1$ 的位置的方案数, 容易做到 $n^4$.
codeforces 2200左右的trees题
CF76A Gift [lct] [mst]
一张图, 每条边有两个属性 $(g_i, s_i)$ . 给定 $G, S$ , 求一棵图的生成树 $T$ , 使得 $G \times \max(g_i) + S \times \max (s_i)$ 最小. ( $i\in T$ )
注意: 图可能包含重边和自环.
$N\le 200, M\le 50000$
考虑把所有 $G$ 和 $S$ 直接乘上去, 就不用管了. 问题变成 $\min \max(g_i)+\max(s_i)$
那么枚举一个最大的 $g$ , 能选的边是一个前缀, LCT! .
题解区里没有LCT? 要不我去写一个? 考虑一个阳间做法, 这题 $N$ 只有200.
CF77C Beavermuncher-0xFF [dp]
给定一棵树, 点 $i$ 的权值为 $k_i$ 求一条从根出发到根结束的路径使得每个点经过次数不大于其权值. 最大化路径长度.
$n, k_i\le 10^5$
$f_i$ 表示进入 $i$ 的子树走一圈回到 $i$ 的最大数量, 那么求 $f_u$ 肯定是走了孩子中 $f$ 递增排休后的一个前缀. 结束了.
CF575B Bribes [ds]
给一棵树, 一些边无方向边权为0, 有向边逆向经过一次边权翻倍. 求按照给定顺序经过 $k$ 个点的边权和. 答案膜.
$n\le 10^5, k\le 10^6$
首先一个显然的 $2log$ 做法, 就是树剖区间乘区间和.
那么正解可以对每一条边单独考虑, 按某方向经过它的代价当然是有若干次子树内与子树外这个切换.
考虑切换是上一次在一个子树区间内, 下一次在子树区间外的个数, 那么把相邻两个数看作一个点, 就转化为二维数点了, 1log.
看题解, 愚蠢了. 直接树上差分做.
CF893F Subtree Minimum Query [线段树合并]
给你一颗有根树, 点有权值, $m$ 次询问, 每次问你某个点的子树中距离其不超过 $k$ 的点的权值的最小值. (边权均为 $1$ , 点权有可能重复, $k$ 值每次询问有可能不同)
强制在线$n\le 10^5, m\le 10^6, a_i\le 10^9$
线段树合并一眼题.
看题解, 原来题目深意在于难为主席树. 不过可以直接考虑就是深度, dfs序两维的数点要强制在线. 那显然就是时间轴建哪的问题, 发现如果时间轴建在dfs序上会寄因为要考虑这个值在区间中出现次数(值有重复). 但只要两维反一下就直接做.
另外给相同点权强行钦定大小整成多个也能做啊.
CF1174F Ehab and the Big Finale [交互] [点分治] [树剖]
给一棵 $n$ 点树, 有一个不知道的点 $x$ , 每次你可以询问 $x$ 到一个点的距离, 或者询问 $x$ 的祖先的哪一个儿子是 $x$ 的祖先. 找出 $x$ .
你可以进行36次操作. $n\le 2\times 10^5$
首先显然是一个 $\log$ 的复杂度. 在树上进行 $\log$ 的常见分治有点/边分治, 树剖.
我们没法添加虚边, 排除边分治.
发现点分治很直接, 我们找到重心, 如果是点的祖先就进入对应子树再找重心, 否则距离可以用来判断当前点是不是祖先. 就做完了. 次数可能多一次随便剪一剪.
CF652E Pursuit For Artifacts [边双] [连通性]
给定一张 $n$ 点 $m$ 边简单无向连通图, 边权是 $0, 1$ . 每条边只能走一次, 求是否存在 $a\to b$ 的路径边权不为0.
$n, m\le 3\times 10^5$
圆方树的重要结论是两个点间简单路径的并集是圆方树上到两个圆点路径距离为1的点. 边双结论相同. 所以缩点之后树上做即可. 所以这题完全可以 $10^5$ 询问吧!
Codeforces 好题 Div. 1-1
看了上面那几个, 又从后面随机了几个, 没意思就换了个题单. 是编号2213 Codeforces 好题 Div. 1-1
尽量秒
CF5E Bindian Signalizing [单调栈] [环转序列]
圆环上有 $n$ 个点, 每个点有权值 $a_i$ , 求点对 $(i, j)$ 数量使得对于圆环上的两个区间 $[i, j]$ 中有至少一个满足 $\max_{k\in [i, j]} a_k\le \min{(a_i, a_j)}$
$n\le 10^6$
考虑一个点能与哪些点形成点对.
如果这个点是全局最大值, 那么能与所有形成点对. 否则不会有一个点同时可以与这个点在两个方向的区间上形成点对.
考虑序列上一个点与前面的点形成点对, 显然维护缀max这件事只需要一个单调栈.
环上需要考虑跨过最后的贡献, 很难写. 最好的办法是把最大值转到最前面按序列做.
CF8E Beads [数位dp] [dp]
求所有长 $n$ 的01串 $s$ 中同时满足字典序不大于其逆序串, 取反串和逆序取反串的串中按字典序排序的第 $m$ 个.
$n\le 50, m\le 10^16$
字典序不大于取反串, $s_1=0$ .
根据最后一位是0或1决定是小于逆序串还是逆序取反串. 分别处理. 假设现在最后一位是0, 处理不大于逆序串.
可以同时两边向中间dp. $f_{i, 0/1}$ 表示前 $i$ 个和后 $i$ 个已经确定, 且填到现在是小于逆序串还是等于逆序串的方案数.
我们会计数了, 但如何求 $kth$ 呢?
假设我们会钦定若干个字符后的方案数–我们确实会, 那么可以直接逐位确定.
看题解: 可以直接折半搜? ! 看来以后看到 $n\le 50$ 要想到这基本上是折半的上界.
CF10E Greedy Change
给定 $n$ 种货币, 求最小的 $w$ 使得贪心求解兑换方式不对(贪心方式就是每次找到不大于它的最大的减去), 或说明不存在.
$n\le 400$
论文题, 汪娟题
todo
CF11D A Simple Task [dp] [状压dp]
求简单无向图的环数.
$n\le 19$
降智了, 这不是图论题这是状压dp看到19该想到的.
那就对每个点跑一遍, $f_{i, S}$ 表示从点 $u$ 出发走到点 $i$ , 走过的点集合为 $S$ , 但很遗憾会把一个环算好多次.
不对每个点跑一次了, 钦定 $S$ 中走过的点最小的为出发节点(所以扩展时只能扩展比这个大的).
最后这样会把一条边算成一个环, 还会把一个环算两次, 所以去掉即可.
CF13E Holes [lct] [分块] [ds]
就是弹飞绵羊
CF15D Map [二维前缀和]
小P要在某个 $n\times m$ 规模的矩阵上建大小为 $a\times b$ 的房子, 已知这个矩阵每一点上的数值 $h_{i, j}$ 代表开始时地面的高度.
若建造 $a\times b$ 房子的地面不一致, 则要把选取的 $a\times b$ 大的矩阵中所有地面都挖低使得和其中一块最低的地面高度一样, 花费是挖的高度和. 小P会重复如下的步骤直至无法再建造更多的房子:
- 找到 $n\times m$ 矩阵中建造房子花费最少的 $a\times b$ 矩阵, 优先选择左上角的矩阵. \
- 输出左上角的位置, 并输出在这里建房子的花费\
- 已经建过房子的地面不能再建房子.
$a, b\le 1000, h_{i, j}\le 10^9$
直接每个点预处理以这个点为左上角的代价排序. 代价处理需要二维前缀和求和, 和一个东西求最小值.
最小值要想求的简单, 感觉一个不错的办法是先竖着求竖着 $b$ 个的最小值再横着合并 $a$ .
然后解决选的不能和已有的覆盖, 这个怎么做呢? 每次选定一个点就把受这个影响的地方暴力覆盖, 复杂度是对的因为一共 $nm$ 个点.
CF19E Fairy [dfs树] [graph]
给一张无向图, 求删一条边变成二分图的方案数.
$n, m\le 10^4$
碰到不知道咋做的图论想dfs树.
dfs树上只有树边和返祖边, 定义一个返祖边对应的只有一条返祖边的环为本源环, 其中本源环为奇环的是坏边, 偶环的是好边, 注意到边能被删当且仅当在所有坏边的本源环上且不在好边的本源环上, 于是树上差分实现判断每条树边被多少坏边的本源环包含即可. 而返祖边只有当奇环总数是 $1$ 的时候删掉那条坏边可行.
这个充要条件是最巧妙的一步, 必须包含所有本源环显然, 不能删掉偶本源环内的是因为去掉之后偶环剩下的部分和奇环剩下的部分组成奇环.
[think] 这个做法的本质是dfs树把无向图排布成一个优秀的结构让返祖边表示本源环.
CF25E Test [greedy] [string]
给出 $s_1, s_2, s_3$ , 求最短的 $t$ 使得其包含给出的三个串作为子串.
$n\le 10^4$
暴力枚举三个子串出现的先后顺序, 最后答案只能是它们接起来. 算接起来的重叠部分可以直接kmp或hash二分.
CF39C Moon Craters [dp]
给出在一个直线上的 $n$ 个圆(位置和半径为 $p_i, r_i$ ), 如果两个圆不相交则可以放在一起(可以包含), 求最多有多少个圆一起.
$n\le 2000$
$f_{i, j}$ 表示区间 $i, j$ 的个数做就行了. 注意直接转移 $n^3$ , 但划分区间的时候可以钦定左半边是一整个圆, 这样只要划分那些有一个左端点是 $i$ 的区间的右端点即可.
CF55D Beautiful numbers [dp] [状态设计]
求 $[l, r]$ 中美丽的数的个数, $x$ 美丽当且仅当 $x$ 可以被每一个非零位整除( $15$ 是美丽的因为可被 $1, 5$ 整除)
$1\le l\le r\le 9\times 10^18$
看着很数位dp. 但要想判断是否能被整除需要知道数值是无法忍受的. 考虑 $1-9$ 的 $lcm$ 只有 $2520$ , $2520$ 的因数(对应当前 $0-9$ 的不同选择情况)只有48个, 于是就 $f_{i, j, k, 0/1}$ 表示前 $i$ 位, 膜 $2520$ 为 $j$ , 当前选择的数要求它被 $2520$ 的第 $k$ 个因数整除, 是否顶到头的方案数.
CF73D FreeDiv [graph] [greedy]
给出一个 $n$ 点 $m$ 边的图和常数 $k$ , 你可以现在图中任意连边, 然后在得到的图中继续连边, 但此时一个点只能连出一条, 同一个连通块只能连 $k$ 条, 求为了得到一个连通图第一步需要连多少边.
$n, k, m\le 10^6$
首先考虑判断继续加边前什么样子时图可以连通. 实际上只要能连的边总数大于需要边数因为我们可以保证不连环.
那么边数总和是 $\dfrac{\sum \min siz_i, k}{2}$ , 需求量是连通块个数-1, 所以 $siz$ 越大越好(取 $\min$ ), 所以每次取两个最小的连通块合并直到满足式子即可.
CF85D Sum of Medians [ds]
维护一个集合, 支持添加一个数, 删除一个数, 或者查询对于将集合内的数从小到大排好序后形成有 $k$ 个数的序列 $a$ , 求
$$\sum_{i}^{(i\le k)\land (i\bmod 5=3)}a_i$$
$n\le 10^5, x\le 10^9$
权值线段树, 维护每个点膜5余0, 1, 2, 3, 4的和即可.
CF86D Powerful array [ds]
莫队板子.
CF93C Azembler [ds]
爆搜idfs板子
CF95E Lucky Country [dp] [自然根号]
如果一个数中不包含除 $4$ 和 $7$ 之外的数字则是幸运数. 有 $n$ 个岛屿, 通过双向道路连接. 这些岛屿被分为几个地区. 每个岛属于恰好一个区域, 同一区域中的任何两个岛之间存在道路, 不同区域的任何两个岛之间没有路径. 如果一个地区的岛屿数量是一个幸运数字, 则这个地区是幸运的. 问最少增加几条道路能创建一个幸运地区.
$n, m\le 10^5$
处理连通块+背包, 但01背包这个过不去.
考虑所有连通块大小之和为 $n$ , 那么经典套路不同的大小有 $\sqrt n$ 种, 所以可以作成 $\sqrt n$ 个物品的完全背包, 结束.
CF103E Buying Sets
放到了网络流选做里.
CF115E Linear Kindom Races [线段树] [dp]
给定序列 $a_n$ 和 $m$ 个区间, 每个区间有价值 $w_i$ , 若要得到区间 $[l, r]$ 的 $w$ 需要支付 $\sum_{l\le i\le r} a_i$ . 求最大收益(收入-支出)
$n, m\le 2\times 10^5$
这是dp题.
很自然的想法是 $f_i$ 表示前 $i$ 个的最大收益, $i$ 如果不修复直接从上一个整过来, 否则 $f_i$ 可能一直修复一个区间到 $f_j$ , 我们钦定没有跨过区间 $[j, i]$ 的端点, 然后贡献就是完整包含在 $[j, i]$ 的区间的 $\sum w_k$ 减去 $\sum a_l$ , 考虑优化.
用线段树维护它, 线段树上每个位置放的就是完整包含在这一段的贡献, 那么就每个下标 $i$ 维护这个决策的值就行了.
CF132E Bits of merry old England
放到网络流选做里.
CF164C Machine Programming
放到网络流选做里
CF176E Archaeology [ds]
就是 异象石.
CF200A Cinema
给出 $n\times m$ 的01矩阵 $A$ , 每个元素初值为 $0$ , $k$ 次操作, 每次给出 $x, y$ , 求离其曼哈顿距离最近的 $0$ 并将其设置为1.
$n, m\le 2000, k\le \min(nm, 10^5)$
KDT?
最无脑的一定是拆开曼哈顿距离, 四个方向各放一个树套树了吧, 可以直接冲.
代码阳间的是, 考虑因为只有 $k$ 个 $1$ , 所以一个 $0$ 距离最近的 $1$ 不超过 $\sqrt k$ , 于是维护每个点离它最近的距离, 然后查的时候暴力枚举等于这个距离的一圈有没有即可. 因为你询问的 $q$ 个点的最近距离的总和是 $\sqrt k$ 的. 就做完了啊.
CF204D Little Elephant and Retro Strings [count]
给定字符串 $s$ , 字符为 $\texttt{01? }$ , $\texttt{? }$ 表示任意. 求多少种方案满足存在两个不相交子串(严格), 且左边的全 $\texttt{1}$ , 右边的全 $\texttt{0}$ .
$k\le \vert s\vert \le 10^6$
统计问题, 设 $f_i, g_i, h_i$ 分别表示前 $i$ 个的最后 $k$ 个全 $\texttt{0}$ , 后 $i$ 个前 $k$ 个全 $\texttt{0}$ , 后 $i$ 个出现过 $\texttt{0}$ 段, 然后方案数就是 $\sum f_ih_{i+1}$
就是要这种可以在多个地方贡献的问题钦定在第一处/最后一处等特殊位置.
CF235C Cyclical Quest
收录在字符串选做上
CF254D Rats [bfs]
一个 $nm$ 的网格图中, 有一些格子是墙, 用 $X$ 表示, 其余格子中, 有一些格子中有*老鼠, 用 $R$ 表示, 其余空格子用 $.$ 表示
现在需要放置两颗手榴弹, 每颗手榴弹初始在格子 $(r_i, c_i)$ 上, 在 $1-d$ 秒内, 每过 $1$ 秒其伤害范围会从现有的每个伤害范围的格子向外扩展一格, 即若 $(a, b)$ 为伤害范围, 则下一秒 $(a+1, b), (a-1, b), (a, b+1), (a, b-1)$ 中不为墙的格子都会变为伤害范围, 当一个有老鼠的格子成为伤害范围, 那个格子的老鼠就会死掉
你需要给出能够杀死所有老鼠的两个手榴弹的放置坐标 $(r_1, c_1)和(r_2, c_2)$ , 如果无解, 则输出 $-1$
$n, m, d$ 为常数, $n, m\le 1000, d\le 8$
疯狂bfs, 先随便找一只老鼠bfs能炸到它的地方, 在这个区域枚举第一个炸弹的位置, 找到一只第一个炸弹炸不到的老鼠, 在这里枚举第二个炸弹的位置, 复杂度 $d^8$
CF263E Rhombus
$n\times m$ 的矩阵 $a$
函数 $f(x, y)=\sum_{i=1}^n\sum_{j=1}^m a_{i, j} \times max(0, k-\vert i-x\vert -\vert j-y\vert )$ , 求 $(a, b)$ 最大化 $f(a, b)$ , 其中 $a\in [k, n-k+1], b\in [k, m-k+1]$
$n, m\le 1000$
todo
qyc推荐
[2022SDFZ省选模拟赛6] 词典 [闵可夫斯基和] [决策单调性] [dp]
一个 $01$ 串 $s$ 是单词当且仅当 $s$ 中不含两个连续的 $0$ .
一个包含 $n$ 个单词的词典是 $n$ 个单词的集合, 且满足其中任意一个单词都不是任意其他单词的前缀.
给定一个词典 $D$ , 定义 $01$ 串 $s$ 的代价 $C(s)=\displaystyle \sum^{k}_{j=1}\lfloor 1+\log_2 j\rfloor$ , 其中 $k$ 是 $D$ 中满足 $s$ 是 $t$ 的前缀的单词 $t$ 的数量. 该词典 $D$ 的代价即为所有 $01$ 串的代价之和.
例如, 考虑一个包含 4 个单词的词典 ${0, 10, 110, 111}$ . 这个词典的代价为 $C(\epsilon)+C(0)+C(1)+C(10)+C(11)+C(110)+C(111)=8+1+5+1+3+1+1=20$ . 这里 $\epsilon$ 表示空串.
求包含 $n$ 个单词的词典的代价的最小值.
多组询问, $n\le 10^{15}, t\le 50000$
神仙题.
考虑把字典插入到一个trie里, 那么因为没有互为前缀所以所有单词叶子, 因为没有两个连续 $0$ 所以左儿子没有左儿子, 树的结构就是
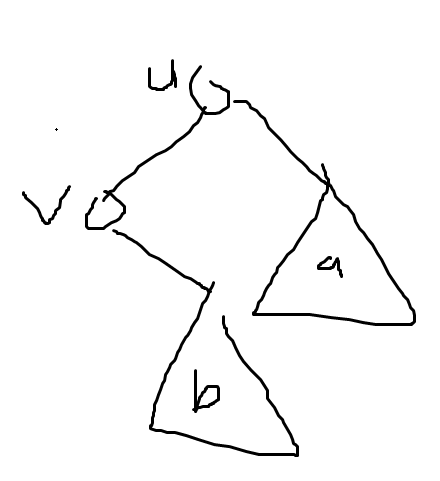
于是考虑dp, 设 $f_{i}$ 表示 $i$ 个叶子的最小代价, 设题面里的代价函数为 $g(k)$ 则有 $f_{i}=g(i)+g(j)+f_j+f_{i-j}$ . 这里 $j$ 是枚举 $b$ 的子树大小, 那么发现 $v$ 的代价是 $g(j)$ , $u$ 的代价是 $g(i)$ .
然后猜测 $g$ 和 $f$ 都是上凸的, 用闵和优化(闵和带来的决策单调性, 两个函数归并每次向后延一段)可以做到 $O(n)$ . 再考虑发现因为 $g$ 的差分只有 $\log$ 段, $f$ 的差分只有 $\log^2$ 段, 所以每次向后延伸一段差分相同的部分, 复杂度就成了 $\log^2$ 的了.
UOJ182. [UR #12]a^-1 + b problem [poly]
区间加, 区间和, 区间取逆元
$n\le 10^5, m\le 6\times 10^4$ , 膜998244353
每个数可以写成 $\dfrac{ax+b}{cx+d}$ , 把 $c$ 化成1, 写成 $a+(b-ad)\dfrac{1}{x+d}$ , 前面的提出来是常量, 所以最后多点求值.
P8371 [POI2001]绿色游戏 [game] [graph] [调整]
绿色游戏是一种两人游戏, 双方分别称 $\text{Ann}$ 和 $\text{Billy}$ . 游戏的内容主要是轮流在棋盘上移动一颗棋子.
棋盘上的点一部分是绿色的, 其余是白色的. 它们全部从 $1$ 至 $a+b$ 编号. 编号 $1$ 至 $a$ 的点属于 $\text{Ann}$ , 编号 $a+1$ 至 $a+b$ 的点属于 $\text{Billy}$ . 每个点都有一些后继点, 均可一步到达. 属于 $\text{Ann}$ 的点的后继点一定属于 $\text{Billy}$ , 反之亦然. 所有的点都至少有一个后继点, 这样总可以往下走一步.
游戏开始时把棋子放在任意的一点 $P$ 上, 然后双方轮流移动棋子至当前所在点(属于移动方)的一个后继点上(属于对手). 游戏由点 $P$ 的拥有者开始, 结束时棋子第二次到达了某一点, 称点 $Q$ . 如果在从点 $Q$ 至点 $Q$ 的一连串移动中, 棋子至少一次被放到绿色点上, 则 $\text{Ann}$ 赢. 若从点 $P$ 开始, 不管 $\text{Billy}$ 如何移动, $\text{Ann}$ 总能保证赢得这次游戏, 则称 $\text{Ann}$ 对起始点 $P$ 有必胜的策略.
请你编写一个程序:
读入对棋盘的描述.
算出 $\text{Ann}$ 有必胜策略的起始点.
$a, b\le 3000$ , 边数 $30000$ , 绿点个数 $green\le 100$
qyc推荐的题.
考虑路径上所有经过的点中, 只让走了两次的那个绿点贡献(必然存在的), 那么如果一个绿点出发有必到达自己策略它是必胜的, 否则就不用管. 而只要从必胜绿点走出去dp就行了. 于是把所有绿点都当必胜的去dp, 每次dp出一个会输的绿点就把它从必胜绿点踢出去接着做, 复杂度是 $green\times m$ .
这么做最后被踢出去的当然真的不能胜利, 而胜利的确实可以走到环上, 所以正确.
[think] POI最爱的钦点-调整法.
from dwt blog
AGC052B Tree Edges XOR [adhoc]
给定 $Tree(n)$ , 保证 $n$ 是奇数, 边有边权 $w_{i, 1}$ , 现在你可以任意次把与一个边相连的其他边的权值异或上这条边的权值, 求是否可以让每条边的边权变为 $w_{i, 2}$ .
$n\le 10^5, w\le 2^30$
最困难的一步在第一步吧. 考虑这个操作本质上在干什么, 发现让边权等于连到它上的两个点权的异或, 则这是在交换相邻两点的点权.
[think] 重新赋值出性质.
[think] 考虑操作本质.
于是现在要给初始状态和结束状态分配点权使得权值集合相同. 考虑点权其实只要确定一个点, 剩下的点权都是确定的这个点异或上一个定值, 于是分别确定1号点权值, 然后解异或方程即可.
ARC126D Pure Straight [dp] [状压dp]
给定 $a_n$ , $a_i\in [1, k]$ , 每次可以交换相邻两个, 求最少次数使得 $a$ 包含子区间值恰为 $1, 2, 3, \ldots, k$ (排好序).
$n\le 200, k\le 16$
$k$ 很小, 说明很状压.
于是想到设 $f_{i, S}$ 表示前 $i$ 个, 最后 $\vert S \vert$ 个已经是排好序的 $S$ 的最小代价.
对于一个元素, 它如果在最终集合里就移动到 $S$ 对应位置, 否则应该整个移动过 $S$ 前面.
发现是错误的–这个元素除了往前移动到 $S$ 前, 还可以向后移动出 $S$ . 于是取个min即可.
CF and Atcoder选糊
看看他们都VP了哪些场.
CF1083 Codeforces Round #526 (Div. 1)
A. The Fair Nut and the Best Path [dp] [树形dp]
给定 $Tree(n)$ , 点有点权 $w_i$ , 边有边权 $c_i$ , 一开始你的分数是0, 走过一个点加 $w_i$ , 走过一个边减 $c_i$ , 任意时刻要求分数 $\ge 0$ , 求走一条链最大化最大分数.
$n\le 3\times 10^5$
直接dp, $f_{i, 0/1}$ 表示当前点作为端点/作为中间点的最大收益即可, 转移显然.
B. The Fair Nut and Strings [greedy]
有 $k$ 个长度为 $n$ 的只含 $a$ 或 $b$ 字符串, 并不知道它们具体是多少, 只知道它们的字典序不小于字符串 $A$ , 同时不大于字符串 $B$ . 定义一个字符串是合法的当且仅当它是这 $k$ 个字符串之一的前缀(如果它是多个串的前缀那么只计算一次). 求最多一共会有多少个合法的字符串.
$n\le 5\times 10^5, k\le 10^9$
就是最大化这 $k$ 个字符的trie点数.
直接贪心, 尽可能多的分配, 和 $k$ 取个min.
C. Max Mex [ds] [线段树] [可合并信息]
给定一棵有 $n$ 个点的树, 每个节点有点权. 所有的点权构成了一个 $0 \sim n - 1$ 的排列.
有 $q$ 次操作, 每次操作 $1$ 为交换两个点的点权, 操作 $2$ 为查询 $Mex(l)$ 值最大的 $Mex(l)$ 值, 其中 $l$ 是树上的一条路径. 定义一条路径 $l$ 的 $Mex$ 值 $Mex(l)$ 为这条路径上最小的没有出现过的自然数.
考虑这个东西是可合并信息: 两条链能不能合并是简单的, 那你就开一个线段树维护走了值在这个区间的点的链, 操作 $1$ 就是单点修改, 操作 $2$ 直接线段树上二分.
实现重点应该是链的合并, 写法包括:
- 枚举新的链的两个端点判断剩下两个是否在上面. 6个lca.
- 枚举新的链的两个端点判断长度是否等于虚数边权和. 4个lca.
- 枚举新的链不是端点的两个点, 分类讨论.
前两个要树剖lca(倍增直接T飞), 第三个不用lca(就是为了和dwt证明不写树剖)
1 | bool check(int a,int b,int c,int d){ |
[trick] 线段树维护的信息也可以是可合并的图信息, 包括树的直径, 链等等
D. The Fair Nut’s getting crazy [ds] [扫描线] [拆式子] [线段树]
给定一个长度为 $n$ 的序列 ${a_i}$ . 你需要从该序列中选出两个非空的子段, 这两个子段满足:
- 两个子段非包含关系.
- 两个子段存在交.
- 位于两个子段交中的元素在每个子段中只能出现一次.
求共有多少种不同的子段选择方案. 输出总方案数对 $10^9 + 7$ 取模后的结果.
需要注意的是, 选择子段 $[a, b]$ 、 $[c, d]$ 与选择子段 $[c, d]$ 、 $[a, b]$ 被视为是相同的两种方案.
$1 \leq n \leq 10^5, -10^9 \leq a_i \leq 10^9$ .
第一眼看成选任意多个子段, 转变成某些不可做题.
假设每个值分别考虑, 那么相当于划分若干段, 限制了四个端点的范围. 问题似乎变成了四维超长方体并体积. 这做个锤子.
假设一个确定的交, 要查第一个满足 $pre$ 在交这个区间的位置. 三维偏序是2log. 发现不可扩展. 不对这不是智障行为吗? 查在这个区间中最大的 $nxt, pre$ 可是简单的很, 也就是如果确定了 $[l, r]$ 作为交, 左右端点范围是 $\min_{i\in [l, r]} nxt_i -1$ 和 $\max_{i\in[l, r]} pre_i +1$
不如考虑画画式子, 为了方便设那个 $\min, \max$ 分别为 $f(l, r), g(l, r)$ 我们要求
$$
\sum_l \sum_r [l<r] (f(l, r)-r)*(l-g(l, r))
$$
可能还有点不重要的常数项(好像没有? ). 拆开, $r\cdot g(l, r)$ 这种东西似乎可以扫 $r$ 解决, 就是区间取max(单调! 变成区间赋值)和区间和.
现在问题是 $f(l, r)\cdot g(l, r)$ , 考虑扫描 $r$ , 问题是区间赋值, 求序列点积. 发现维护区间 $a, b$ 和答案就是线性变换.
就这也配3500
E. The Fair Nut and Rectangles [dp] [斜率优化]
给定 $n$ 个矩形, 左下角为 $(0, 0)$ , 右上角为 $(x_i, y_i)$ , 每个矩形有权值 $a_i$ , 矩形互不包含, 求选择若干矩形使得并的面积减权值和最大.
$n\le 10^6, x_i, y_i\le 10^9$
考虑你画一画, 发现如果我们从左往右选, 因为 $y_i$ 递减, 每个矩形的贡献就是上一个矩形到它的距离乘 $y_i$ , 于是就直接dp, $f_i$ 表示前 $i$ 个矩形选的最大值, 然后斜率优化转移.
F. The Fair Nut and Amusing Xor [ds] [greedy] [分块]
给定 $a_n, b_n$ 和常数 $k$ , 每次可以选择长 $k$ 的子段全异或上一个值, 求把 $a$ 变成 $b$ 的最小次数或说明无解. 有 $q$ 次单点修改, 每次修改结束输出结果.
$n, q\le 2\times 10^5$
设 $c_i=a_i\mathrm{xor} b_i$ , 就成了从全 $0$ 变成 $c$ 的次数.
然后因为区间异或想到差分数组设为 $d$ , 每次修改 $d$ 的两个位置.
然后考虑每个 $\bmod k$ 等价类是独立的, 那么此时一个等价类的次数就是大小减前缀异或和等于自己的数的个数.
那这个就好做了, 相当于区间异或, 查询0的个数. 每个整块存出现次数和异或标记散块暴力即可.
[trick] 固定长 $k$ 可以分成若干等价类
CF1687 Codeforces Round #796 (Div. 1)
A. The Enchanted Forest [greedy]
魔法森林可以被抽象成一条有着 $n$ 个节点, 从 $1$ 到 $n$ 标号的数轴. 在魔理沙出发之前, 她的好友帕秋莉运用魔法去侦测了每个节点上的蘑菇数量, 分别为 $a_1, a_2, \dots, a_n$ .
在第 $0$ 分钟的时候, 魔理沙可以从任意一个节点出发. 在每一分钟的时候, 她将会做以下事情:
- 她将从节点 $x$ 移动到节点 $y$ ( $\vert x-y\vert \leq 1$ , 即 $y$ 可能等于 $x$ )
- 她将会收集节点 $y$ 上的所有蘑菇.
- 魔法森林中每个节点会再生长出一个蘑菇.
注意, 她不能在第 $0$ 分钟的时候收集蘑菇.
现在魔理沙希望知道她在前 $k$ 分钟的时候, 最多能收集到多少个蘑菇. 请你帮帮她.
考虑如果她 $k\ge n$ , 是不是直接答案一样模拟.
如果 $k<n$ , 那么一定不会回头, 新长出来的部分是固定的, 于是求最大的长 $k$ 的和.
B. Railway System
收录在图论选做里.
C. Sanae and Giant Robot [greedy]
给定 $a_n, b_n$ 和 $m$ 个区间 $[l_i, r_i]$ , 每次可以把一个区间的 $a_i$ 赋值为对应位置的 $b_i$ 当且仅当这么做 $\sum a_i$ 不变. 求是否可以把 $a$ 变成 $b$ .
$n, m\le 2\times 10^5$
考虑每个位置先减去 $b_i$ , 那么相当于每次选一个和为 $0$ 的区间赋值成0, 问最后能不能全变成0.
相当于前缀和, 每次选择相同的两个数把中间变得也相同. 感觉这个模型比较好.
考虑如果某一次赋值的时候不是赋成0, 那么一定不优–你必然需要一个更大的把它搞成0, 或者你必然不会用中间的部分和区间外组成匹配对.
那就简单了, 每次找个0的对暴力操作, 想怎么做怎么做.
D. Cute number [math]
给定 $a_n$ , 找到最小的 $k\ge 0$ 使得 $\forall i, a_i+k$ 是可爱的. 定义一个数 $x$ 是可爱的当且仅当 $x-g(x)<f(x)-x$ , 其中 $f(x), g(x)$ 分别是第一个大于, 小于等于它的数.
$n\le 10^6, a_i\le 2\times 10^6$ , $a$ 不降.
相当于值域被划分成若干段, 每个段的前一半是合法的. 或者说每个数处在一个 $[x^2, x(x+1)]$ 中.
考虑 $a_1$ 对应的 $x$ 是 $v$ 一定合法, 所以只有 $v$ 段.
那么枚举一个 $x_1$ ( $a_1+k$ 所对应的 $x$ ), 合法的 $a_1+k$ 是一个区间, 对接下来的每个 $a_i$ , 这个区间能到的 $x$ 段必然只有一个(它们的 $x$ 只会更大, 长度只会更长, 并且一个 $x$ 两边一段都是不合法的). 于是求个交就能得到答案.
考虑优化, 当枚举到 $x$ 时, 两个差在 $x$ 之内的数必然在同一块, 把它们缩起来, 分析复杂度的话考虑差分数组 $c_n$ , $c_i$ 在 $x<c_i$ 的时候没有被缩起来, 所以总代价是 $\sum c_i=v$ . 复杂度 $O(v)$ .
E. F. todo
CF1152 Codeforces Round #554 (Div. 2)
A. Neko Finds Grapes
智障题.
B. Neko Performs Cat Furrier Transform
模拟
C. Neko does Maths
给定两个正整数 $a, b$ , 找到非负整数 $k$ 使 $a+k$ 与 $b+k$ 的最小公倍数最小, 如有多解输出最小的 $k$ .
$a, b\le 10^9$
降大智了.
考虑最小公倍数很离谱, 但最大公约数比较好: 两者差始终为定值, 最大公约数是差的约数.
于是直接枚举最大公约数, 算出最小的 $k$ 然后更新最小公倍数即可.
D. Neko and Aki’s Prank
求所有长度为 $2n$ 的合法括号序列组成的trie的最大匹配. 合法括号串是仅有 $\texttt{()}$ 组成且匹配的. 膜 $998244353$ .
$n\le 1000$ .
考虑一个子树可以由 $(d, v)$ 表示为高度为 $d$ , 并且括号和是 $-v$ .
可以转化为求最大独立集.
$f_{d, v, 0/1}$ 表示这样的子树, 有没有选根即可. $n^2$ .
看到题解区里由点离谱的构造: 直接选所有深度为偶数的边和其父节点的连边(冲突保留一条), 然后用卡特兰数.
E. Neko and Flashback
对于序列 $a_n$ 和 $p_{n-1}$ , 构造 $b_i=\min(a_i, a_{i+1}), c_i=\max(a_i, a_{i+1}), b’i=b{p_i}, c’i=c{p_i}$ . 给定 $b’, c’$ 求 $a$ 或判断无解.
$n\le 10^5, v\le 10^9$
看错题了, $b$ 和 $c$ 的重排方式是相同的.
考虑那么任意一个 $b_i, c_i$ 相当于告诉你 $a_i, a_{i+1}$ 两个数连着, 是充要的, 于是每个值建图跑欧拉回路即可.
F. Neko Rules the Catniverse
给定参数 $n, k, m$ , 你需要求有多少个大小为 $k$ 的序列 $a$ 满足如下三个条件:
- 任意两个元素其权值不同.
- 对于任意 $i$ 满足 $1\le i\le k$ 有 $1\le a_i\le n$ .
- 对于任意 $i$ 满足 $2\le i\le k$ 有 $a_i\le a_{i-1}+m$ .
答案对 $10^9+7$ 取模.$1\le k\le \min(n, 12)$ , $1\le m\le 4$ .
F1 (Small Version)
$1\le n\le 10^5$
显然你应该扫值域插入着dp, 插入的要求是这个位置的前一个位置在不小于 $i-m$, 发现插入更大的元素无法缩小两个数的间距, 所以要求一开始插入的时候就让前一位置不小于 $i-m$. 于是显然你至少要记录 $f_{i, j}$ 表示前 $i$ 个数选了 $j$ 个, 此时你能插入的位置取决于在 $[i-m, i-1]$ 中的元素选了几个, 因为这个要转移所以你要记录选了谁(不然向上一位不知道掉出去的是谁), 所以 $f_{i, j, S}$ 表示最小的 $i$ 个数, 选了 $j$ 个, $[i-m, i-1]$ 中选了集合 $S$. 复杂度 $nk2^m$
F2 (Big Version)
考虑两层之间转移固定, 直接矩阵快速幂就是 $(k2^m)^3\log n$.
CF1793
好久文化课了
A. Yet Another Promotion
显然
B. Fedya and Array
构造最短的序列 $a$, 满足所有 $a_i>a_{i-1}, a_{i+1}$ 的 $a_i$ 和为 $x$, 同理小于的和为 $y$.
$n\le 10^5$
考虑并观察样例, 如果 $a<0<b$, 构造是显然的, 直接用两个峰做完了, 那么整体平移一下就问题解决, 长度是 $2(b-a)$
C. Dora and Search
给定排列 $a_n$, 求任意一个子区间满足左右端点不是区间内的最大/最小值
$n\le 2\times 10^5$
求每个数向左/向右作为最大/最小值的范围, 一个右端点的限制是左端点小于某个位置, 一个左端点的限制是右端点大于某个位置, 于是把左端点排序, 就扫右端点维护左端点即可吧
官方题解更简单: 从整个序列开始收缩, 显然如果当前区间 $[l, r]$ 的某个端点 $x$ 不满足条件, 则包含这个端点的前/后缀不满足, 于是直接收缩一个, 不断重复即可.
D. Moscow Gorillas
给定排列 $a_n, b_n$, 求有多少个区间 $[l, r]$ 满足 $\mathrm{mex}(a_l\ldots, a_r)=\mathrm{mex}(b_l\ldots, b_r)$
$n\le 2\times 10^5$
那么肯定考虑枚举 $mex$ 求数量.
mex等于 $x$ 的要求是小于 $x$ 的必须包含且不包含 $x+1$, 从小到大枚举 $x$, 是不是随便做了.
E. Velepin and Marketing
给定 $n$ 个元素和 $m$ 个集合, 每个元素有属性 $a_i$, 把元素分到集合中, 要保证每个集合中有至少一个元素, 且若一个元素 $i$ 所在的集合大小大于 $a_i$, 则元素 $i$ 是开心的, 求最大开心元素个数.
$n\le 3\times 10^5$
考虑对 $a$ 排序+二分答案 $x$, 显然最后要开心的是最小的 $x$ 个.
那么对于后 $x$ 个元素, 每个元素放入一个集合, 此时如果剩下元素, 就把剩下的和所有前 $x$ 个放到一个集合check, 否则从小往大放元素, 每次一个集合全部满足要求就切换到下一个集合. 这个部分可以预处理
F. Rebrending
给定序列 $a_n$, $q$ 次询问区间 $[l, r]$ 中最小的 $\vert a_i-a_j\vert$.
$n\le 3\times 10^5$
是的大原题.
对于每个位置 $a_i$, 从左到右考虑 $j$ 是否能形成贡献, 此时假设现在已经有 $i, j$, 那么对于元素 $k$, 显然应该与 $i, j$ 近的那个贡献, 于是如果和 $i$ 贡献, 那么 $\vert a_k-a_i\vert \le \dfrac{1}{2}\cdot\vert a_i-a_j \vert$, 所以只有 $n \log n$ 对
直接主席树和二维数点复杂度2log
AT_cf17_final CODE FESTIVAL 2017 Final
D
收录在greedy
E
有字符串 $S$, 按照顺序多次进行以下 $N$ 种操作:
- 操作 $i$: $S$ 的第 $l_i$ 个字母到第 $r_i$ 个字母分别变为它们的下一个字母. (
a变成b,b变成c・・・); 假设z的下一个字母是a.判断是否可以把 $S$ 变成回文.
$\vert S\vert\le 10^5$
容易想到差分, 回文串的差分要求对称位置互为相反数.
那么每个区间操作 $[l, r]$ 看作 $l\to r+1$ 形成一张图, 注意这里边是双向的(转 $25$ 下), 这就非常好, 于是可以在连通块内任意分配值, 只要判断每个连通块的和是对的就行了.
F
选择 $n\in [1000, 2000], k\ge 1$, 构造矩阵 $A_{n\times k}$, 满足 $A_{i, j}\in [1, N], A_{i, j}\ne A_{i, j’}$, 任意两行恰有一个相同数字, 每个数一共出现 $k$ 次.
考虑 $n$ 行形成的完全图, 则有 $\dfrac{n(n-1)}{2}$ 条边, 而每个数出现 $k$ 次, 贡献 $\dfrac{k(k-1)}{2}$ 条边, 所以 $(n-1)=k(k-1)$.
然后手动模拟 $k=3, k=4$, 得到策略: 考虑枚举最小值, 第一行先写下 $1\ldots k$, 然后第一列写下一串 $1$, 在后面跟上递增的序列, 保证 $1$ 的部分是对的, 接下来对每个 $2\ldots k$, 每个数写 $k-1$ 个到第一行, 后面对于数 $i$, 从上面以 $1$ 为最小值的第二行到第 $k$ 行的表格中纵向加 $1$, 横向加 $i-1$ 的走着取.
这个策略只能 $n$ 是质数, 然后就可以了.
G
考虑以下游戏.
- 准备一个具有 $N$ 个格子和许多石头的列.
- 首先, 在格子 $i\ (1\ \leq\ i\ \leq\ N)$ 中放置 $a_i$ 个石头.
- 玩家可以进行”选择恰好有 $i$ 个石头的格子 $i$, 并在那里放置的所有石头, 以及从格子 $1$ 到格子 $i-1$ 的 $i-1$ 个格子中的石头, 每个格子各放置 $1$ 个石头”的操作, 可以进行任意次数.
- 最终, 剩余的石头数量的总和是分数.
对于长度为 $N$ 的数列 $a$ 进行这个游戏时, 将其作为分数考虑的最小值为 $f(a)$.
在该情况下, 对于所有长度为 $N$, 每个元素为 $0$ 到 $K$ 之间的数列 $a$, $f(a)$ 的总和是多少? 由于答案可能非常大, 因此请使用 $1000000007\ (=\ 10^9+7)$ 进行取模.$K\le N\le 100$
画一条 $y=x$ 的线, 一旦一个位置高出它, 就再也不可能被操作了, 所以最优步骤一定是每次操作最低的能操作的位置. 同时每次操作都是让总和小 $1$, 直接数一共操作多少次.
$f_{i, j}$ 表示后 $i$ 个数操作了 $j$ 次, 则当前位置可以操作 $t_i=(a_i+j)/i$ 次, $f_{i, j+(a_i+j)/i}=f_{i+1, j}$
H
在北冰洋, 海上漂浮着 $H$ 行 $W$ 列的冰块. 我们将该区域视为网格, 并将第 $i$ 行和第 $j$ 列的方格表示为 $Square(i, j)$. 漂浮在每个方格中的冰块不是薄冰就是厚冰.正方形网格外没有冰块.
$Square(i, j)$ 处的冰块可以用以下三种字符表示:
+此方格是薄冰.#此方格是厚冰.P此方格是企鹅所在地, 为薄冰.夏天一到, 因温度上升和薄冰的不稳定性, 薄冰将会一个接一个的融化消失. 我们定义, $Square(i, j)$ 处的薄冰在同时不满足以下两个条件时就会融化:
- $Square(i-1, j)$ 和 $Square(i+1, j)$ 都有冰块.
- $Square(i, j-1)$ 和 $Square(i, j+1)$ 都有冰块.
现在, 一个不怀好意的人来到了这里. 他可以用锤子砸厚冰, 使其变为薄冰. 请问, 他至少要砸多少块厚冰, 才能使企鹅所在处的冰块融化消失?
$1 \le H, W \le 40$.
困难
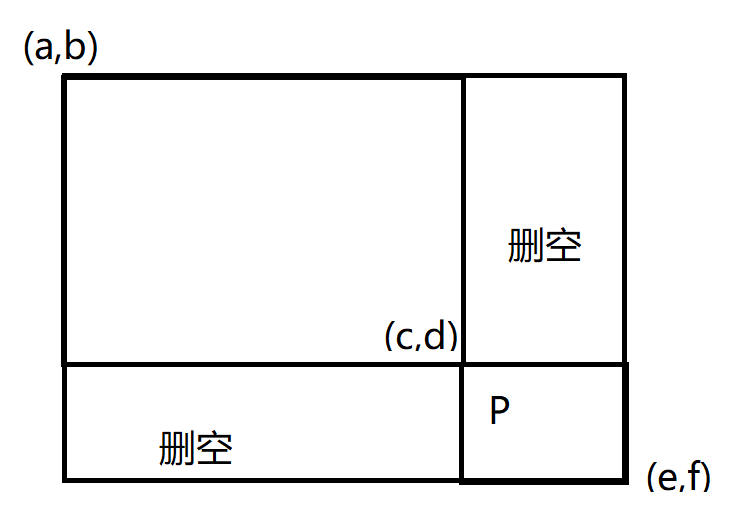
用 $(x_1, y_1), (x_2, y_2)$ 表示左上角 $x_1, y_1$, 右下角 $x_2, y_2$ 的矩形.
注意到当 $(a, b)(e, f)$ 中两个矩形 $(a, b)(c, d), (c, d)(e, f), (a<c<e, b<d<f)$, 当 $(a, d)(c, f)$ 与 $(c, b)(e, d)$ 全空了的时候, 就互不相干了.
所以dp, $f_{a, b, c, d}$ 表示矩形 $(a, b)(e, f)$ 的答案, 每次转移的时候枚举 $(c, d)$, 分成四部分, 递归到有P的那个矩形, 删空侧面的两个矩形.
NOIP选做
P7916 [CSP-S 2021] 交通规划
考虑显然同种颜色形成若干连通块, 问题就是去找连通块之间的分界线. 于是转成对偶图(分界线画出来就是割掉若干条边啊因为), 那么相邻异色附加点对在图外围的部分当成一个点, 就成了两两匹配这些点, 代价是匹配的点对之间的最短路长度. 于是直接跑出两两之间距离然后暴力dp(容易发现相交一定不优, 所以是简单区间dp), 合法性显然. 对于最优性, 可以考虑分界线不会是中间一个圈, 同时一定不会从同色点之间出发, 那么方案都可以得到这样的分界线.
P7116 [NOIP2020] 微信步数
容易想到计算第 $i$ 步后哪些位置出发的还存在, 对这个统计答案.
发现只要记录每一维左右两侧最大位移, 因为每一维上存在的点是一个区间, 那么答案就是 $\prod_i r_i-l_i+1$, 复杂度是 $nwk$.
考虑走完 $n$ 步是一个周期, 假设走完一轮增加的向量为 $a$, 上一轮到这一步时的最大位移向量 $l, r$ 就要分别和 $l+a, r+a$ 取min/max, 取决于 $a$ 在每一维上的正负, 对于确定的 $a$, 其实是加一个常向量. 于是第 $i$ 步时的贡献就成了关于轮数的 $k$ 次多项式
P5665 [CSP-S2019] 划分
容易想到一个 $n^3$ 暴力dp, 容易发现对任意一个区间, 一定满足最后一段尽量小的是这个区间内的最优解.
于是dp时若原本记录 $f_{i, j}$ 表示前 $i$ 个位置最后一个区间左端点是 $j$, 则最优的 $j$ 唯一(本来就是更小的 $j$ 能转移到更多答案, 只保留一个即可).
那就简单了, 设前缀和数组为 $s$, $i$ 位置的最优决策点为 $p_i$, 则要求 $f_i=\min_{j, s_i>2s_j-s_{p_j}} f_j+(s_i-s_j)^2$, 因为 $s_i$ 单增, 所以上一个单调队列维护即可.
P5666 [CSP-S2019] 树的重心
至少做到大常数单log是简单题, 容易想到对每个点求作为了多少次重心, 那么根据重心定义要求最大的子树小于一半, 于是可以直接列出删除的部分的大小满足的不等式, 然后线段树合并维护子树大小集合即可.
P5021 [NOIP2018 提高组] 赛道修建
上来一个明显的二分答案, 然后考虑判断是否能到这个数, 第一反应是dp, 在节点 $u$ 考虑向上延一条, 剩余的在下面两两配对.
但会爆炸而且注意到这里可以贪, 如果到节点 $u$, 底下延上来的大于答案直接加上, 然后从最小值开始每次找第一个加起来满足条件的配对, 最后传上去剩下的最大的. 因为要在满足答案最大的情况下传上去的尽可能大, 那么从小往大的过程中, 一定不会有 $a$ 可以配对而不配(说明存在 $b>a$, 使得 $b$ 配对后原来和 $a$ 配对的可以传上去, 显然不可能).
P5659 [CSP-S2019] 树上的数
先考虑一个顶点的情况, 发现依次删掉 $u$ 连向 $v_1\ldots v_k$ 的边后, 点 $v_i$ 上的值转移到 $v_{i+1}$ 上, $v_k$ 转移到 $u$ 上, $u$ 转移到 $a_1$ 上, 形成一条链的关系, 那么如果让 $v_i\to v_j$ 就确定了这两条边删除顺序是 $v_i$ 后紧接着删除 $v_j$, 如果 $u\to v_i$ 就说明 $v_i$ 是第一个删的, $v_i\to u$ 说明是最后一个删的. 那么对每个点用并查集维护这些链, 并记录每个点的 $front_u, back_u$ 表示此点第一个和最后一个删的边, 考虑判定不合法的情况:
- $u\to v$:
- $u$ 有已经确定的 $front_u$
- $v$ 不是某条链头的第一个($v$ 要作为 $front_u$ 必须是第一个)
- $back_u$ 存在且如果让 $v$ 成为 $front_u$ 则 $front_u, back_u$ 会到同一条链中且链外还有其他元素
- $v\to u$(作为结尾和作为开头是对称的)
- $u$ 有已经确定的 $back_u$
- $v$ 不是某条链头的最后一个
- $front_u$ 存在且如果让 $v$ 成为 $back_u$ 则 $front_u, back_u$ 会到同一条链中且链外还有其他元素
- $f\to u\to v$($u$ 作为中转点)
- 加入这个关系后 $u$ 的 $front_u$ 和 $back_u$ 到同一条链中, 且链外还有其他元素
- $v$ 不是 $front_u$, $f$ 不是 $back_u$
- $v, f$ 当前不在同一条链, 且 $v$ 是链头, $f$ 是链尾
因为满足以上条件的情况下必然存在合法解(剩下的边随便乱连串起来)要求最小字典序, 所以考虑逐个确定数字 $i$ 能移动到的最小的节点, 直接枚举 $u$, 枚举 $v$, 判断链的复杂度是 $n^3$ 的, 考虑对每个 $u$ 去 $dfs$ 整个树找到能作为结尾的 $v$ 再从中选择, 复杂度变为 $n^2$
P3960 [NOIP2017 提高组] 列队
首先观察到操作就是第 $x$ 行, 第 $n$ 列的后缀往前移动一格, 再配一个单点修改. 那么容易想到单独维护最后一列, 于是拿出来一个放到最后就可以用平衡树简单实现. 然后发现点很多不能把点都插到平衡树里, 想到直接上一个珂朵莉树维护连续区间就结束了.
注意到维护这个东西其实可以bit, 开一个长 $n+q$ 的bit然后支持倍增和求和即可. 那么动态开点也能做. 空间多1log.
最后可以离线处理每行的答案就是这一行原来元素的询问, 在线处理新元素, 这样只要维护最后一行和每行新元素.
P1315 [NOIP2011 提高组] 观光公交
首先转换一下贡献, $\sum_p T’_p-T_p=\sum_i t_i cnt_i-\sum T_i$, 其中 $p$ 是枚举的人, $i$ 是枚举点, $t$ 表示到达某点的时间, $T’$ 表示某人下车时间.
考虑一个点的出发时间, 应该是到这个点的时间 $t_i$ 和最晚上车的人的时间 $maxt_i$ 的max, 可以先求一遍这个, 然后若 $t_i\le maxt_i$, 则这个加速对更大的 $i$ 无影响, 而有影响的部分就是区间 $cnt$ 和. 于是维护区间直接贪心即可做到 $nk$
upd:
假设读者已经都会了费用流的做法, 因为是费用流, 所以关于流量是凸的, 我们考虑WQS二分+增量费用流+反悔贪心完成:
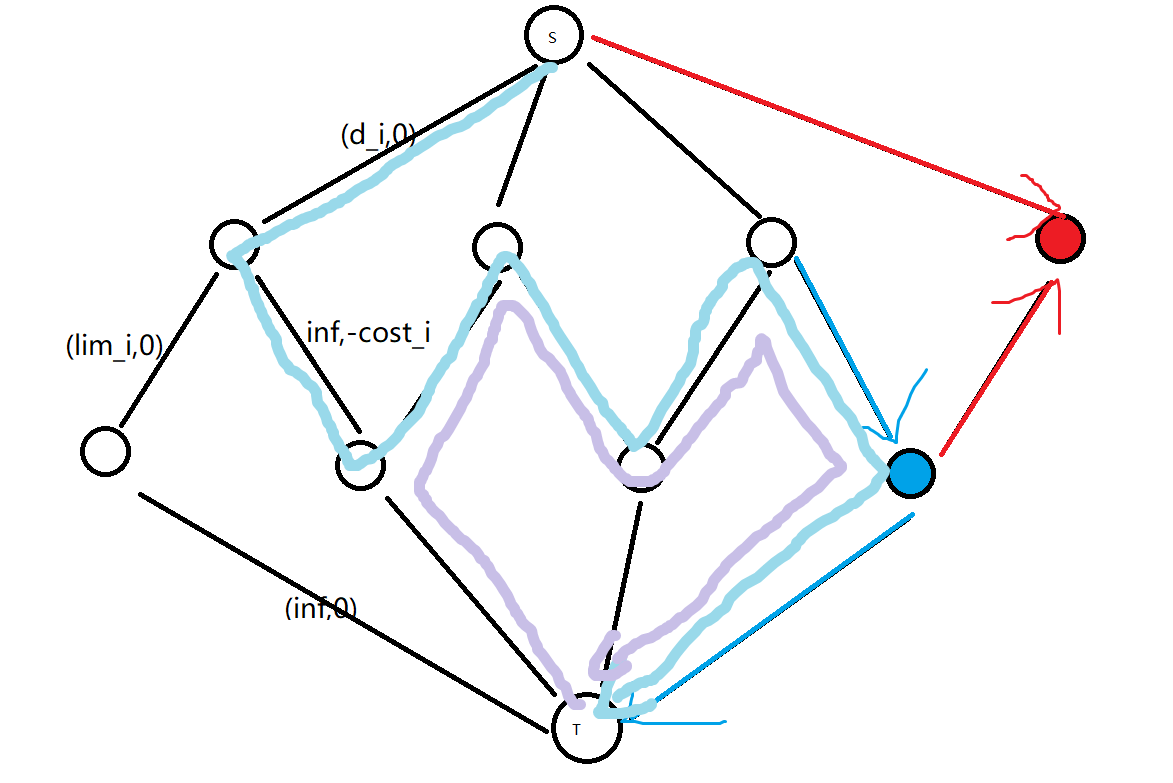
那么如图, 加一个与S相连的点时要保证红边的方向, 于是发现没有可行的负环/增广路, 增加蓝色的点 $v$ 的时候增广路的形式是 $S\to u\to v\to T$(浅蓝), 负环是 $T\to u\to v\to T$(浅紫), 只有这两种决策, 于是问题解决, 开两个堆维护与 $S$ 相连, 且 $S$ 到它的边上还能流的点和与 $T$ 相连, 且它到 $T$ 的边有流量的点, 用线段树维护中间的边的流量, 用前缀和维护代价和, 每次取出堆顶, 计算两种决策的流量和代价, 然后更新流量和答案. 因为要控制流量, 找增广路的时候要给代价额外加上二分的常数 $C$.
这里很好的性质就是由于我们的决策, 一条非汇边满了之后不可能再退流, 一条汇边在它之后空了之后不可能在有流量, 所以只要每次取出堆顶暴力check, 不满足直接弹就是对的. 又因为处理每个负环和增广路的时候, 我们至少会让一条边的流满, 所以模拟费用流的复杂度是 $n\log n$ 的, 最后上一个WQS二分, 复杂度成了 $n\log n\log k$, 现在可以出 $k\le 10^9$ 了!
P3959 [NOIP2017 提高组] 宝藏
首先这数据范围看着就是状压dp. 显然如果加点顺序确定, 加的边就是确定的, 问题是dp加点的时候我们需要它的深度. 深度集合是难以压缩的, 依赖于图的结构, 于是考虑直接把最后一次加点的深度作为状态, 每次加入同一个深度的所有点, 于是 $f_{i, S}$ 表示集合 $S$ 中的点已经加入, 最深的点深度为 $i$. 显然这样会算错, 但是同样显然算错了的只会更劣, 不影响答案统计. 复杂度 $n^3 3^n$
P5022 [NOIP2018 提高组] 旅行
树就是直接dfs, 基环树粗暴法是直接枚举断一条边, 仔细分析的话注意到流程一定是入环, 访问环上一边, 回溯, 访问另一边, 回溯只有在当前环上点要走的下一个环上点是所有除了父亲以外的点中最大时才可能(否则从小到大访问, 回溯了这里的子树就无法访问了), 同时在走的时候记录如果此时回溯下一个到的是谁, 跟本来会访问的比对即可.
P5023 [NOIP2018 提高组] 填数游戏
这个数据范围让我怎么看怎么想状压啊!
考虑dp, 那么发现我们肯定是按照对角线推进, 限制包括: 每条对角线从上到下递增, 同时要求若 $(i-1, j)=(i, j-1)$, 则 $(i, j)$ 为右上角的矩形中所有的对角线分别相等(否则两条路径在 $i, j$ 处交叉再到下面再次交叉就不合法了)
SDOI题选做
P4620 [SDOI2018] 荣誉称号
休闲游戏玩家小 $Q$ 不仅在算法竞赛方面取得了优异的成绩, 还在一款收集钻石的游戏中排名很高.
这款游戏一共有 $n$ 种不同类别的钻石, 编号依次为 $1$ 到 $n$. 小 $Q$ 已经玩了这款游戏很久了, 对于第
$i$ 种钻石, 他已经收集到了 $a_i$ 个. 这款游戏最大的亮点就是, 钻石只有一种获得途径, 那就是从商城中购买. 具体来说, 第 $i$ 种钻石的单价为 $b_i$ 点券. 为了鼓励玩家充值, 每种钻石都没有数量上限, 只要肯充钱, 就可以拥有任意多的钻石. 但是这款游戏并没有开发 “丢弃道具” 功能, 因此小 $Q$ 不能通过丢弃钻石去完成任务.最近这款游戏推出了一个限时成就任务, 完成任务的玩家可以获得荣誉称号, 而完成任务条件则是:
给定正整数 $k$ 和 $m$, 对于任意一个整数 $x (x\ge 2^k)$, $a_{x}+a_{\lfloor\frac{x}{2}\rfloor}+a_{\lfloor\frac{x}{4}\rfloor}+a_{\lfloor\frac{x}{8}\rfloor}+. . . +a_{\lfloor\frac{x}{2^k}\rfloor}$ 都要是 $m$ 的倍数.高玩小 $Q$ 当然想完成这个限时成就任务, 但是在充钱之前他想知道他究竟需要多少点券才能完成这个任务. 请写一个程序帮助小 $Q$ 计算最少需要的点券数量.
- $1 \le T \le 10$,
- $1 \le k \le 10$ 且 $2^k \le n$,
- $1 \le p \le min(n, 100000)$, $10000 \le SA, SB, SC \le 1000000$,
- $1 \le A, B, ai, bi \le 10^7$.
- $n\le 10^7, m\le 200$
看到 $\dfrac{x}{2^k}$ 可以把序列先搬到二叉树上.
然后就要满足任意长 $k$ 的链的和都是 $m$ 的倍数, 那么考虑一条链在尾端加入在链首删除, 就要保证新链尾与原链首同余, 于是第 $k+1$ 层往后的方案都是由前 $k$ 层唯一确定的, 可以先处理出 $w_{i, j}$ 表示深度大于 $k$ 且模 $k$ 为 $i$ 的所有层中的点都调整到模 $m$ 为 $j$ 的代价和, 那么接下来dp前 $k$ 层的方案, 设 $f_{u, i}$ 表示 $u$ 的子树, 所有叶子到 $u$ 的和为 $i$ 的最小代价(由刚才处理的 $w$ 得出), 答案即为 $f_{1, 0}$, 后面dp的复杂度 $2^km^2$, 前面预处理 $w$ 是 $n+mk$
P5359 [SDOI2019] 染色
最简单的暴力肯定是 $f_{i, c_1, c_2}$ 表示前 $i$ 行最后两个数分别是啥.
考虑如果把没数的一段压起来处理, 这样转移时 $c_1, c_2$ 有一个是确定的, 就可以只记录一维, 而上下两位置都没数的方案只和两头两列有关, 根据数的关系不同, 确定了前两个不同的数后后面可以有 $7$ 种, 去掉上下对称后可以精简到 $5$ 种, 而预处理长 $n$ 的空段两边是哪种情况的复杂度 $g(n, 0/1/2/3/4)$ 是线性的. 于是复杂度变成了 $nc$.
然后考虑数据结构优化dp转移, 就是单点修改/查询, 全局加/乘/赋值/查询, 随便做了.
P4618 [SDOI2018] 原题识别
给定一棵树, 询问树链上本质不同颜色数以及一条链的所有子链的本质不同颜色数之和.
$n, q\le 10^5$, 数据随机
随的方法是 $p$ 个点之后随机挂叶子, 众所周知的结论意味着一个点到主链期望 $\log n$ 步.
先考虑序列上怎么做操作 $2$, 那么要询问一个点在 $[1, a]$, 一个点在 $[1, b]$ 中的答案, 让 $a<b$, 记录每个点上次出现位置 $pre_i$, 则当且仅当 $pre_i\lt l\le i\le r$ 时点有贡献, 那么对于 $[1, a]$ 的点 $i$ 就是 $2(i-pre_i-1)(a-i+1)+(i-pre_i)(b-a)$, 对于 $a, b$ 中的点就是 $pre_i<a(b-i+1)$, 第一个直接乱维护, 第二个两维限制可以接着主席树, 都是维护下 $i, pre_i, i^2, ipre_i$ 的和就行了.
然后上树, 就要用刚才的随机性质了, 那么设 $u=lca(a, b), dis(u, a)<dis(u, b)$, 此时根据一开始分析树的形态 $dis(u, a)<\log n$, 那么可以先原样照搬的解决掉 $x, y$ 有祖先关系的情况, 现在问题来到 $x, y$ 分别在 $u\Rightarrow a, u\Rightarrow b$ 上, 此时从上到下 $u\Rightarrow a$ 上的一个点作为左端点, 相当于每次加入一个点 $x$ 钦点它被选, 而 $u\Rightarrow b$ 上一个点本来的贡献应该是 $dep_{pre_i}<dep_u$, 那只要查长链上最浅的 $i$ 满足 $a_i=a_x$ 即可.
比较套路比较麻烦题, 基本上是基于随机树的性质+ $i, pre$ 乱搞.
P5360 [SDOI2019] 世界地图
$n\times m$ 网格图, 边有边权, 第一列和第 $m$ 列相连, $q$ 次询问删除第 $[l, r]$ 列中的点后的最小生成树权值和.
$n\le 100, m\le 10000, q\le 10000$
考虑这是让你合并一个前缀一个后缀的mst, 直接合并边集复杂度和 $m$ 有关肯定爆炸, 考虑逐条加入 $(i, 1)$ 和 $(i, m)$ 之间的边, 则要判断新边和这条环上最大边比谁大然后换掉最大边, 那么一个前缀可能被替换掉的边就是这个前缀Kruskal重构树上所有 $(i, 1)$ 的点的虚树上的非叶子点, 每次把这些边, 新加入的 $(i, 1), (i, m)$ 边和后缀的 $O(n)$ 条边拿出来跑Kru就能合并, 问题变为怎么获得两边的信息.
对于一个前缀, 维护其第一列和最后一列的点的虚树上的非叶子点也就是可能删掉的边, 那么每次新加一列这个操作可以像刚才上面一样Kru, 并获得新的可能被删掉的边.
P4607 [SDOI2018] 反回文串
“回文串什么的最讨厌了……”
小 $Q$ 讨厌任何形式的回文串:
如果一个字符串从左往右读和从右往左读是一样的, 那么小 $Q$ 讨厌它; 例如 $aa$ 和 $aba$.
对于一个字符串来说, 若将某个前缀子串移除并拼接到字符串的尾部, 能得到一个小 $Q$ 讨厌的字符串, 那么小 $Q$ 也会讨厌原来的这个字符串; 例如 $aab$ 和 $baa$.
那么问题来了, 如果任意字符串只可以由 $k$ 种已知的字符组成, 那么长度为 $n$ 的所有字符串里, 有多少字符串是小 $Q$ 讨厌的?
答案可能很大, 你只需要给出答案对 $p$ 取模的值.
$1 \le T \le 10, 1 \le n \le 10^{18}, 1 \le k \le n, 10^9 \le p \le 2^{30}$
摆结论: 一个字符串的不同轮换数是循环节长度, 一个回文串的循环节也一定是回文串.
但是长 $m$ 的回文最小循环节 $t$ 贡献并非 $m$, 比如 $abba$ 轮换两下是 $baab$, 于是 $abba$ 和 $baab$ 会把它们的循环数两遍, 实际上对于任意一个 $m$ 是偶数的最小回文循环节, 将其平移 $\dfrac{m}{2}$ 位会得到另一个回文串, 所以只贡献 $\dfrac{m}{2}$, 而奇数回文串照常贡献 $m$.
于是设长 $m$ 的回文且无更小循环节的串数量是 $f(m)$, 其中每个的贡献是 $g(m)$, 就是要求 $\sum_{d\vert n}f(d)g(d)$
但是 $f(d)$ 是不好求的, 由这个无更小循环节容易想到反演, 即
$$
h(d)=k^{\lfloor \dfrac{d}{2} \rfloor}=\sum_{p\vert d} f(p)\Longrightarrow h=f1, f=h\mu
$$
注意到其实你可以只在约数上卷 $\mu$, 用一个经典trick, 卷 $\mu$ 等价于对所有质数 $p$ 卷上每个
$$
m_p(x)=\begin{cases}
1, x=1\
-1, x=p\
0, otherwise
\end{cases}
$$
对 $a_n$ 进行这个相当于对每个数 $i$ 另 $a_{ip}: = a_{ip}-a_i$, 也就是说对所有约数求 $f(p)$ 的时候只会用到质因子的 $m_p$, 可以直接求出所有约数的 $f(p)$ 了, 就解决问题了.
我是智障, 卷 $\mu$ 就是狄利克雷差分, 卷 $1$ 是狄利克雷前缀和. 怎么把这个忘了.
P4605 [SDOI2018] 物理实验
小 T 这学期有物理实验课, 为了顺利完成下一节课的实验, 他打算在课前对实验内容进行预习.
这次实验在一个二维平面上进行, 平面上放置了一条无限长的直线导轨, 导轨上放置了一个长为 $L$ 的激光发射器, 激光发射器会向导轨两侧沿导轨垂直方向发射宽度为 $L$ 的激光束.
平面上还放置了 $n$ 个挡板, 每个挡板可以看作是一条线段, 现在每个挡板都不和直线导轨接触, 且
和直线导轨的夹角不超过 $85 \degree$, 任意两个挡板也不会相互接触, 激光束不能穿透这些挡板, 并且会被挡板吸收掉, 不会被挡板反射出去.小 T 想确定一个激光发射器的位置使得被激光束照射到的挡板长度之和最大, 你需要帮小 T 算出这
个最大值.
- $T \le 100$
- $1 \le n \le 10^4$,
- $1 \le L \le 2 \times 10^9$,
- 所有坐标的绝对值不超过 $10^9$.
显然先把坐标轴转回来, 让导轨是横轴, 然后用线段的横坐标可以把轴分成若干段, 每一段的贡献是导轨两侧离它最近的线段的 $\cot$ 值乘长度.
求最近的线段是简单的, 因为保证不相交, 所以任意位置线段的相对顺序不变, 所以上一个 $set$, 扫描线, 在 $x_1, x_2$ 处插入/删除线段即可.
最后求最大值的话容易发现最优情况下激光光束的一遍一定贴着一个端点, 双指针秒了.
P4619 [SDOI2018] 旧试题
求 $\sum_{i=1}^A\sum_{j=1}^B\sum_{k=1}^C d(ijk) \pmod {10^9+7}$, 其中 $d$ 为约数个数.
$A, B, C\le 1\times 10^5$
上来先反演.
[trick]求 $d(ijk)$ 考虑其每个约数都可以拆成 $xyz$, 其中 $x, y, z$ 分别为 $i, j, k$ 的约数, 然后为了不重钦定选质因子 $p^k$ 的时候如果够就在 $x$ 中选, 不够了再到 $y$ 中选剩下 $p^{k-c_x}$, 其中 $c_x$ 为 $x$ 中 $p$ 的次数, 而不在 $x$ 中选这个质因子, 再不够同理到 $z$ 中选则每个质因子只出现一次, 所以
$$
d(ijk)=\sum_{x\vert i}\sum_{y\vert j}\sum_{z\vert k} [x\perp y][y\perp z][z\perp x]
$$
于是再把互质用莫反搞掉
$$
\begin{gathered}
\sum_i \sum_j \sum_k d(ijk)\
=\sum_i \sum_j \sum_k \sum_{x\vert i} \sum_{y\vert j} \sum_{z\vert k} [x\perp y][y\perp z][z\perp x]\
=\sum_{x} \sum_{y} \sum_{z}[x\perp y][y\perp z][z\perp x] \lfloor \dfrac{A}{x}\rfloor\lfloor \dfrac{B}{y}\rfloor\lfloor \dfrac{C}{z}\rfloor\
=\sum_{x} \sum_{y} \sum_{z}\sum_{d_1\vert x, d_1\vert y}\mu(d_1)\sum_{d_2\vert y, d_2\vert z}\mu(d_1)\sum_{d_3\vert x, d_3\vert z}\mu(d_1) \lfloor \dfrac{A}{x}\rfloor\lfloor \dfrac{B}{y}\rfloor\lfloor \dfrac{C}{z}\rfloor\
=\sum_{d_1}\mu(d_1)\sum_{d_2}\mu(d_2)\sum_{d_3}\mu(d_3)\sum_{\mathrm{lcm}(d_1, d_2)\vert x}\dfrac{A}{x}\sum_{\mathrm{lcm}(d_2, d_3)\vert y}\dfrac{A}{y}\sum_{\mathrm{lcm}(d_3, d_1)\vert z}\dfrac{A}{z}\
=\sum_{d_1}\mu(d_1)\sum_{d_2}\mu(d_2)\sum_{d_3}\mu(d_3)\sum_{a\mathrm{lcm}(d_1, d_2)\le A}\dfrac{A}{a\mathrm{lcm}(d_1, d_2)}\sum_{b\mathrm{lcm}(d_2, d_3)\le B}\dfrac{B}{b\mathrm{lcm}(d_2, d_3)}\sum_{c\mathrm{lcm}(d_3, d_1)\le C}\dfrac{C}{a\mathrm{lcm}(d_3, d_1)}
\end{gathered}
$$
上面所有除法都带取整. 然后你考虑 $d_1, d_2, d_3$ 三元组的贡献, 要求他们 $\mu$ 都不是 $0$, 并且 lcm 小于某值, 那么枚举一个lcm值把所有这个lcm对应的点连边, 发现边数 $8\times 10^5$ 量级, 而有贡献前提是构成三元环, 所以上三元环计数, 每统计到一个三元环加上其答案即可. (然后要算 $\sum_k \dfrac{A}{ak}=\dfrac{\frac{A}{a}}{k}$)可以预处理.
P3705 [SDOI2017] 新生舞会
简单题, 分数规划基本上就是二分之后移项变成一个线性规划问题去判定, 而这个线性规划问题就是若匹配 $i, j$ 则代价 $a_i-b_imid$, 费用流即可.
P3702 [SDOI2017] 序列计数
先考虑求不含质数的, 把单个数的GF写出来是 $\sum a_ix^i$, 其中 $a_i$ 为 $m$ 以内模 $p$ 为 $i$ 的质数个数, 然后暴力算它的 $n$ 次幂就是 $p^2\log n$ 过了
P3704 [SDOI2017] 数字表格
求 $\prod_{i=1}^n\prod_{j=1}^m Fib(\gcd(i, j))$, $n, m\le 10^6$.
转而枚举 $\gcd(i, j)$, 则求 $\prod_d Fib(d)^{g(d)}$, 其中 $g(d)=\sum_{i=1}^\frac{n}{d}\sum_{j=1}^\frac{m}{d} [\gcd(i, j)]=1=\sum_k \mu(k)\dfrac{n}{dk}\dfrac{m}{dk}$.
带回去, 得到
$$
ans=\prod_{T=kd}\prod_d (Fib(d)^{\mu(\frac{T}{d})})^{\frac{n}{T}\frac{m}{T}}
$$
里面的部分暴力是 $\sum_T \sqrt T$ 是 $n\sqrt n$ 的不太行, 考虑对每个 $d$ 把 $Fib(d)^{\mu(k)}$ 乘到 $kd$ 去, 调和级数过了.
P3703 [SDOI2017] 树点涂色
首先看到区间赋值, 你应该想到树剖颜色段均摊的性质, 那么树剖之后操作 $1$ 均摊改线性个段, 那么每次修改段的时候对一个颜色段深度最浅的点子树加就能做操作 $3$, $x, y$ 路径权值可以差分, 反正不差分也不困难.
P3707 [SDOI2017] 相关分析
简单题, 拆开那个大式子最后就是让你维护 $\sum x_iy_i, \sum x_i^2, \sum x_i, \sum y_i$, 然后修改的话要一个区间价标记一个区间加下标标记, 互不干扰的, 并且对和的影响都是显然的.
P3780 [SDOI2017] 苹果树
夏天近了, 又到了恋爱的季节, 小Q家门前的苹果树上结满了红红圆圆的苹果.
这株苹果树是一个有着 $n$ 个结点的有根树, 其中结点被依次编号为 $1$ 至 $n$. $1$ 号结点为根, 其余每一个结点的父结点一定是某个编号较小的结点. 每一个结点上都有一些苹果, 第 $i$ 个结点上有 $a_i (a_i > 0)$ 个苹果, 每取走其中一个苹果就可以得到 $v_i (v_i > 0)$ 的幸福度(若在这个结点取走 $k \leq a_i$ 个苹果, 则可以收获 $kv_i$ 的幸福度). 如果在一个结点取走了至少一个苹果, 则必须要在其父结点处取走至少一个苹果.
现在, 给定正整数 $k$, 请从树上取走若干苹果. 如果总计取走了 $t$ 个苹果, 且所有取了至少一个苹果的那些结点的最大深度为 $h$(这里规定根结点的深度为 $1$), 则要求 $t-h \leq k$. 问最大可以收获多少的幸福度? (这些幸福度全都归属于恋爱中的小Q. )
$n\le 20000, k\le 5\times 10^5$
好奇妙
首先理解一下题意, 可以把 $t-h\le k$ 相当于先给一条链每个点选一个且是免费的, 然后再选剩下的是付费的, 答案可以认为是不包含这条链的背包和这条链上让 $a_i: = a_i-1$ 的背包合并.
但是不包含一条链的背包我们不会做, 显然这条链一定到叶子, 发现如果把树画到平面上, 按照dfs序, 链左边的点dfs序小于当前叶子, 右边的点大于dfs序, 那么只要在dfs序上正反两遍合并背包得到 $f, g$ 两个背包, 再卷上链上的背包 $h$ 即是答案, 而这两些多重背包都可以优化到 $nk$
问题是, 如果只卷两个背包因为我们只想知道一项复杂度是 $k$ 的, 但是合并三个背包就 $k^2$ 了, 于是我们希望能把这条链上的背包 $h$ 处理到 $f$ 或 $g$ 上, 于是考虑在进入一个节点的时候(入栈)向背包插入 $a_i-1$ 且不要求至少选一个, 退出该节点的时候要么插入 $1$ 要么相当于这个点及其子树都不选.
最终复杂度 $nk$
[trick] 树的dfs序可以把树按照一条到叶子的链分成两半
P3779 [SDOI2017] 龙与地下城
求 $y$ 个均匀随机变量 $w_i$ 的和在 $[a, b]$ 中的概率, 每个变量是 $[1, x]$ 中的整数.
$x\le 20, y\le 2\times 10^5, a, b\le xy$, 精度要求绝对误差 $0. 013579$
好大的误差? 干嘛用的?
首先暴力是不是, 把它们卷起来, 上个FFT的话可以做到 $xy\log(xy)$, 有点过不了.
好大的误差干嘛用的? 注意到当 $Y$ 很大的时候结果服从正态分布, 那么方法一是直接积出来, 方法二是FFT过程中不断丢掉很小的数使得多项式长度不长.
[trick] 精度大就是让你丢0的.
P3785 [SDOI2017] 文本校正
给定两个字符串 $s, t$, 要求看能否把 $s$ 划分成 $3$ 个非空的段 $s_1, s_2, s_3$, 使得 $t$ 是以某种顺序连接这 $3$ 个段得到的.
$n\le 10^6$
按照 $s$ 的顺序分类:
$t=s_1+s_2+s_3$ 是显然的, $s_2+s_3+s_1$ 和 $s_3+s_1+s_2$ 都是一个轮换判定也是显然的.
对于 $t=s_1+s_3+s_2$ 和 $s_2+s_1+s_3$, 就是要判断去掉一个前缀之后两个字符串是可以划分两段后相等的, 考虑 $s_2+s_1+s_3$ 的情况, 枚举 $s$ 第一段的右端点 $i$, 求 $s$ 剩下的部分和 $t$ 的lcp值 $l_i$, 设 $t$ 的第一段的右端点为 $j$, 剩下部分与 $s$ 的lcp为 $l’_j$, 则要满足 $i\le l’_j, j\le l_i, i+j\ge L$, 那么二维数点了. 而 $l_i, l’_j$ 用exkmp解决.
还剩下 $t=s_3+s_2+s_1$ 的情况, 就要找 $i, j, i+j<n, s_{1\ldots i}=t_{n-i+1\ldots n}, s_{n-j+1\ldots n}=t_{1\ldots j}$ 满足 $n-lcp(s_{i+1\ldots n}, t_{j+1\ldots n}\le i+j$.
第三个限制是两个字符串在反串 SAM parent 树上lca的最大长度限制, 考虑从大到小枚举 $i$, 从小到大不断加入可行的 $j$, 每次把 $t_{j+1\ldots n}$ 到根的路径上的点 $u$ 都和 $n-j-maxlen_u$ 取min, 或者查找 $s_{i+1\ldots n}$ 到根的路径上的最小值是否小于 $l$, 要做到单log要上全局平衡二叉树.
THUSC 2024
T1
给定 $n, L, d_n$, 求
$$
\sum_{(a_1, \dots a_n), \forall a_i\le d_i} \max(0, (a_1\mathrm{xor}a_2\ldots a_n)-L)
$$
$10$ 组数据, $n\le 10$, $d_i\le 10^{18}, L\le 10^9$
感觉T1不会很难所以写了 $4^n\log V$, 听说mikefeng也是 $4^n\log V$, 不过这玩意有 $d^2\log V$ 啊!
但是怎么正解就是 $4^d\log V$, 有点拉了.
从高往低枚举第一个存在至少一个数没顶上界的位置, 考虑因为异或的性质, 更低位就均匀了(总可以控制当前位置使得低 $k$ 位取任意值, 每个值方案数均为其他数任选的方案数), 于是现在就数 $C\sum_i \max(0, a+i-L)$ 的形式, 就做完了. 复杂度 $d\log V$
T4
赛时看错题了///fn
第1-4是要处理怎么做乘法, 前三个做法是爆搜剪枝
第四个注意到 $x+998244353=2^{30}$ 才能满分? ? ?
第5-7个点是区间求和
第8是狄利克雷前缀和, 9是FMT
第10个是随机数据